| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 1:30 sri, 21. 9. 2005 Naslov: Postano: 1:30 sri, 21. 9. 2005 Naslov: |
    |
|
|
5. zadatak
formule koje ti zivot znace su:
(1) [latex]\Phi(-x)=1 - \Phi(x)[/latex]
(2) [latex]P(a \leq X \leq b) = \Phi \left( \frac{b - \mu}{\sigma} \right) - \Phi \left( \frac{a - \mu}{\sigma}\right)[/latex]
ti imas [latex]N(6.1,1.2)[/latex]i znas da ih je 10% palo
oznacimo sa [latex]x_p[/latex] vrijednost sl. varijable koja znaci granicu izmedju pada i prolaza, iz [latex]N(6.1,1.2)[/latex] imamo [latex]\sigma ^ 2 = 1.2 \rightarrow \sigma = 1.449[/latex]
sredimo formulu (2), radi kraceg pisanja ostavljam simbole sto dulje mogu
[latex]P(0 \leq X \leq x_p) = \Phi \left( \frac{x_p - \mu}{\sigma} \right) - \Phi \left( \frac{0 - \mu}{\sigma}\right)[/latex]
zbog uvjeta od 10% padnutih, znamo da je [latex]P(0 \leq X \leq x_p) = 0.1[/latex]
[latex]0.1 = \Phi \left( \frac{x_p - \mu}{\sigma} \right) - \Phi \left( \frac{- \mu}{\sigma}\right)[/latex]
zbog (1) imamo
[latex]0.1 = \Phi \left( \frac{x_p - \mu}{\sigma} \right) - \left(1- \Phi \left( \frac{\mu}{\sigma}\right) \right)[/latex]
[latex]0.1 = \Phi \left( \frac{x_p - \mu}{\sigma} \right) - 1 + \Phi \left( \frac{\mu}{\sigma}\right)[/latex]
[latex]0.1 + 1 - \Phi \left( \frac{\mu}{\sigma}\right)= \Phi \left( \frac{x_p - \mu}{\sigma} \right)[/latex]
jer je [latex]\frac{\mu}{\sigma}=\frac{6.1}{1.449}=4.2 > 3[/latex] za koji je [latex]\Phi (3) = 0.999[/latex], a [latex]\Phi(x)[/latex] je rastuca fja, to za 4.2 uzimamo da je [latex]\Phi(4.2) = 1[/latex] i imamo
[latex]0.1 = \Phi \left( \frac{x_p - \mu}{\sigma} \right)[/latex]
zbog (1) imamo
[latex]1 - 0.1 = 0.9 = \Phi \left( \frac{\mu - x_p}{\sigma} \right)[/latex]
odatle iz tablica slijedi da je
[latex]\frac{\mu - x_p}{\sigma} = 1.28[/latex] (0.8997 je blize 0.9 nego 0.9015)
[latex]x_p = \mu - 1.28 \cdot \sigma = 6.1 - 1.85 = 4.25[/latex]
potrebno je rijesiti [b]5[/b] zadataka
ako ste ostavili 4.25 (ili 4.23 za uvrstavanje za 0.9015) izgubili ste 2 boda
sto se tice ostalih zadataka, asistent je rekao da su vec danas negdje dostupni (utorak) ali nisam zapamtila gdje...
5. zadatak
formule koje ti zivot znace su:
(1) 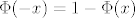
(2) 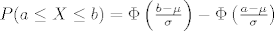
ti imas 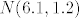 i znas da ih je 10% palo i znas da ih je 10% palo
oznacimo sa 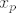 vrijednost sl. varijable koja znaci granicu izmedju pada i prolaza, iz vrijednost sl. varijable koja znaci granicu izmedju pada i prolaza, iz 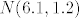 imamo imamo 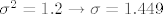
sredimo formulu (2), radi kraceg pisanja ostavljam simbole sto dulje mogu
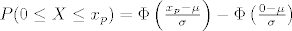
zbog uvjeta od 10% padnutih, znamo da je 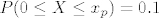
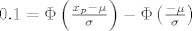
zbog (1) imamo
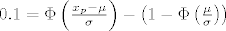
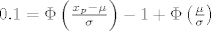
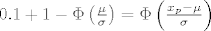
jer je 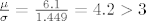 za koji je za koji je 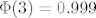 , a , a 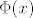 je rastuca fja, to za 4.2 uzimamo da je je rastuca fja, to za 4.2 uzimamo da je 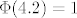 i imamo i imamo
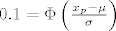
zbog (1) imamo
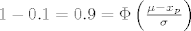
odatle iz tablica slijedi da je
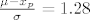 (0.8997 je blize 0.9 nego 0.9015) (0.8997 je blize 0.9 nego 0.9015)

potrebno je rijesiti 5 zadataka
ako ste ostavili 4.25 (ili 4.23 za uvrstavanje za 0.9015) izgubili ste 2 boda
sto se tice ostalih zadataka, asistent je rekao da su vec danas negdje dostupni (utorak) ali nisam zapamtila gdje...
_________________
It's not who you love. It's how.
Zadnja promjena: Nesi; 4:14 sri, 21. 9. 2005; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 3:16 sri, 21. 9. 2005 Naslov: Postano: 3:16 sri, 21. 9. 2005 Naslov: |
    |
|
|
4. zadatak
[latex]A = \left( \begin{array}{cc}
X_1 & X_2 \\
X_3 & X_4
\end{array}\right)[/latex]
m-ca je singularna kada je det A = 0 tj [latex]X_1 X_4 = X_2 X_3[/latex]
to znaci da lijeva i desna strana moraju biti istog predznaka
kada je to [b]-[/b] imamo mogucnosti:
[latex]X_1, X_2 > 0; X_4, X_3 < 0[/latex]
[latex]X_1, X_3 > 0; X_4, X_2 < 0[/latex]
[latex]X_1, X_2 < 0; X_4, X_3 > 0[/latex]
[latex]X_1, X_3 < 0; X_4, X_2 > 0[/latex]
kada je to [b]+[/b] imamo mogucnosti:
[latex]X_1, X_4, X_2, X_3 > 0[/latex]
[latex]X_1, X_4, X_2, X_3 < 0[/latex]
[latex]X_1, X_4 > 0; X_2, X_3 < 0[/latex]
[latex]X_1, X_4 < 0; X_2, X_3 > 0[/latex]
sve skupa 8 mogucnosti koje nam pasu, a ukupno ih ima 2^4 = 16
znaci vjerojatnost je 8/16 = 1/2
ofkors, ako nisam fulala
varijancu racunamo:
[latex]X = \left( \begin{array}{ccc}
-2 & 0 & 2\\
1/4 & 1/2 & 1/4
\end{array}\right)[/latex]
[latex]E(X) = -2 \cdot 1/4 + 0 \cdot1/2 + 2 \cdot 1/4 = 0[/latex]
[latex]X^2 = \left( \begin{array}{cc}
0 & 4\\
1/2 & 1/2
\end{array}\right)[/latex]
[latex]E (X^2) = 0 \cdot 1/2 + 4 \cdot 1/2 = 2[/latex]
[latex]Var X = E(X^2) - (E(X))^2 = 2 - 0 = 2[/latex]
ofkors, ako nisam nesto fulala
4. zadatak
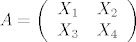
m-ca je singularna kada je det A = 0 tj 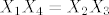
to znaci da lijeva i desna strana moraju biti istog predznaka
kada je to - imamo mogucnosti:
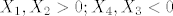
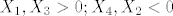
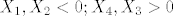
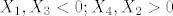
kada je to + imamo mogucnosti:
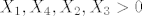
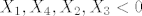
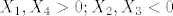
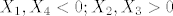
sve skupa 8 mogucnosti koje nam pasu, a ukupno ih ima 2^4 = 16
znaci vjerojatnost je 8/16 = 1/2
ofkors, ako nisam fulala
varijancu racunamo:
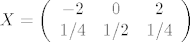
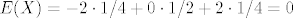
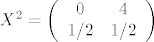
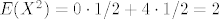
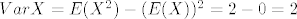
ofkors, ako nisam nesto fulala
_________________
It's not who you love. It's how.
Zadnja promjena: Nesi; 4:45 sri, 21. 9. 2005; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 3:44 sri, 21. 9. 2005 Naslov: Postano: 3:44 sri, 21. 9. 2005 Naslov: |
    |
|
|
3. zadatak
u svakom slucaju se radi o geometrijskoj vjerojatnosti i zapravo treba racunati cudne povrsine....
[img]http://student.math.hr/~nesi/javno/rok-uvis-2.png[/img]
povrsina u koju novcic moze upasti je plava ofarbana povrsina + zuti kruzni odsjecci
vjerojatnost da novcic u nju upadne je (plava povrsina) / (povrsina trokuta) (jer mozemo cijeli R2 poplocati trokutima, pa onda gledamo stanje samo unutar jednog trokuta)
plavu povrsinu dobijemo kao povrsinu ofarbanog velikog kruga [b]-[/b] povrsina malog zutog kruga [b]-[/b] povrsina zutih kruznih odsjecaka
podaci:
duljina stranice trokuta = 1
radijus novcica - 1/12 = r = 0.083
radijus trokutu upisane kruznice = R = 1/3 visine trokuta (jer je trokut jednako str pa je teziste = ortocentar = sve sto treba) = sqrt(3)/6 = 0.2887
radijus velikog kruga = radijus trokutu upisane kruznice + radijus novcica = R + r = 0.3717
radijus malog kruga = radijus trokutu upisane kruznice - adjius novcica = R - r = 0.2057
i sada je vj = vjerojatnost upada u plavo podrucje = (Pkruga(R+r) - Pkruga(R-r) - 3*Podsjecka(R+r,alfa))) / (P trokuta stranice 1)
alfa dodje iz pravokutnog trokuta (kada prepilite ovaj nacrtani trokut unutar svega na 2 i to tako da je piljenje okomito na stranicu pocetnog trokuta)
hipotenuza je R + r
alfa/2 je izmedju nje i katete od R
so, cos (alfa/2) = R / (R + r)
so, [latex]alfa = 2 arccos \left( \frac{R}{R + r} \right) = 78.08[/latex] stupnja
Pkruga(R+r) = 0.434
Pkruga(R-r) = 0.133
Podsjecka(R+r,alfa) = r^2/2 * (pi * fi / 180 - sin fi) = 0.069 * (1.363 - 0.978 ) = 0.0265
P trokuta stranice 1 = sqrt(3)/4 = 0.433
so, vj = (0.434 - 0.133 - 3*0.0265) / (0.433) = 0.2215 / 0.433 = 0.5115
1. zadatak ima rijec dokaz pa ga kao takvog bas ne volim... prepustam to nekom drugom
ako imam gresaka, bila bih zahvalna da ih netko pokaze....
3. zadatak
u svakom slucaju se radi o geometrijskoj vjerojatnosti i zapravo treba racunati cudne povrsine....

povrsina u koju novcic moze upasti je plava ofarbana povrsina + zuti kruzni odsjecci
vjerojatnost da novcic u nju upadne je (plava povrsina) / (povrsina trokuta) (jer mozemo cijeli R2 poplocati trokutima, pa onda gledamo stanje samo unutar jednog trokuta)
plavu povrsinu dobijemo kao povrsinu ofarbanog velikog kruga - povrsina malog zutog kruga - povrsina zutih kruznih odsjecaka
podaci:
duljina stranice trokuta = 1
radijus novcica - 1/12 = r = 0.083
radijus trokutu upisane kruznice = R = 1/3 visine trokuta (jer je trokut jednako str pa je teziste = ortocentar = sve sto treba) = sqrt(3)/6 = 0.2887
radijus velikog kruga = radijus trokutu upisane kruznice + radijus novcica = R + r = 0.3717
radijus malog kruga = radijus trokutu upisane kruznice - adjius novcica = R - r = 0.2057
i sada je vj = vjerojatnost upada u plavo podrucje = (Pkruga(R+r) - Pkruga(R-r) - 3*Podsjecka(R+r,alfa))) / (P trokuta stranice 1)
alfa dodje iz pravokutnog trokuta (kada prepilite ovaj nacrtani trokut unutar svega na 2 i to tako da je piljenje okomito na stranicu pocetnog trokuta)
hipotenuza je R + r
alfa/2 je izmedju nje i katete od R
so, cos (alfa/2) = R / (R + r)
so, 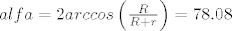 stupnja stupnja
Pkruga(R+r) = 0.434
Pkruga(R-r) = 0.133
Podsjecka(R+r,alfa) = r^2/2 * (pi * fi / 180 - sin fi) = 0.069 * (1.363 - 0.978 ) = 0.0265
P trokuta stranice 1 = sqrt(3)/4 = 0.433
so, vj = (0.434 - 0.133 - 3*0.0265) / (0.433) = 0.2215 / 0.433 = 0.5115
1. zadatak ima rijec dokaz pa ga kao takvog bas ne volim... prepustam to nekom drugom
ako imam gresaka, bila bih zahvalna da ih netko pokaze....
_________________
It's not who you love. It's how.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Casper
Forumaš(ica)


Pridružen/a: 02. 04. 2005. (14:45:29)
Postovi: (7E)16
Spol: 
Lokacija: Krk
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
|
| [Vrh] |
|
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
|
| [Vrh] |
|
|











