| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Jadran
Gost
|
 Postano: 15:07 uto, 27. 9. 2005 Naslov: Pomoć oko roka 27.9.2005 MA2, hitno! Postano: 15:07 uto, 27. 9. 2005 Naslov: Pomoć oko roka 27.9.2005 MA2, hitno! |
    |
|
|
Trebam pomoć oko ovih zadataka jer sam na komisiji pa bi me mogli to pitati šta nisam znao.
Hvala vam svima unaprijed!
ANALIZA 2
27. 9. 2005.
1.
Odredite parametar alfa eR takav da funkcija f: R — R definirana formulom:
f(x)={ alfacosx, za x<=0
arctg(lnx), za x > 0 }
bude neprekidna. U kojim točkama je tako dobivena funkeija derivabilna?
2.
Doka da za svaki x e [0, PI=180 ] vrijedi nejednakost
sin x + (1/2)sin 2x + (1/3)sin 3x = 0.
3.Ispitajte konvergira li sljedeći nepravi integral:
∫(na [0,+∞]) dx / [ (1+x^(1/2))(1+x^(1/3))(1+x^(1/4)) ]
4.
Dokažite da na grafu funkcije f(x) = (2x + 2) / (x^2 - 2x+2) postoje tri točke infleksije i da sve
one leže na jednom pravcu.
Trebam pomoć oko ovih zadataka jer sam na komisiji pa bi me mogli to pitati šta nisam znao.
Hvala vam svima unaprijed!
ANALIZA 2
27. 9. 2005.
1.
Odredite parametar alfa eR takav da funkcija f: R — R definirana formulom:
f(x)={ alfacosx, za x⇐0
arctg(lnx), za x > 0 }
bude neprekidna. U kojim točkama je tako dobivena funkeija derivabilna?
2.
Doka da za svaki x e [0, PI=180 ] vrijedi nejednakost
sin x + (1/2)sin 2x + (1/3)sin 3x = 0.
3.Ispitajte konvergira li sljedeći nepravi integral:
∫(na [0,+∞]) dx / [ (1+x^(1/2))(1+x^(1/3))(1+x^(1/4)) ]
4.
Dokažite da na grafu funkcije f(x) = (2x + 2) / (x^2 - 2x+2) postoje tri točke infleksije i da sve
one leže na jednom pravcu.
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 15:33 uto, 27. 9. 2005 Naslov: Postano: 15:33 uto, 27. 9. 2005 Naslov: |
    |
|
|
Sutra na žalbama u 11:30 vam mogu dati primjerak rješenja zadataka (da sad ne prepisujem ovdje) i objasniti ako nešto nije jasno.
Ako je pak hitnije, onda samo ideje:
1. Izjednače se lijevi i desni limes u 0 te f(0) da se dobije alfa=-pi/2. Onda se racunaju lijeva i desna derivacija u 0. Lijeva je 0, desna +oo (dakle zapravo ne postoji). Prema tome, f je derivabilna na R\{0}, ali nije u 0.
2. Racuna se minimum funkcije f:[0,pi]->R, f(x)=lijeva strana. Nadju se vrijednosti u svim kritičnim točkama i zakljuci se da je minimum =0 (postize se na rubu segmenta).
3. (b) Konvergira. Usporedi ga se s integralom
[latex]\displaystyle\int_{1}^{+\infty}\frac{dx}{x^{\frac{13}{12}}}[/latex]
(naime 1/2+1/3+1/4=13/12), a on konvergira zbog 13/12>1.
4. Izračuna se druga derivacija i nacrta tablica. Provjera da tri točke leže na jednom pravcu je klasika.
Sutra na žalbama u 11:30 vam mogu dati primjerak rješenja zadataka (da sad ne prepisujem ovdje) i objasniti ako nešto nije jasno.
Ako je pak hitnije, onda samo ideje:
1. Izjednače se lijevi i desni limes u 0 te f(0) da se dobije alfa=-pi/2. Onda se racunaju lijeva i desna derivacija u 0. Lijeva je 0, desna +oo (dakle zapravo ne postoji). Prema tome, f je derivabilna na R\{0}, ali nije u 0.
2. Racuna se minimum funkcije f:[0,pi]→R, f(x)=lijeva strana. Nadju se vrijednosti u svim kritičnim točkama i zakljuci se da je minimum =0 (postize se na rubu segmenta).
3. (b) Konvergira. Usporedi ga se s integralom
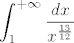
(naime 1/2+1/3+1/4=13/12), a on konvergira zbog 13/12>1.
4. Izračuna se druga derivacija i nacrta tablica. Provjera da tri točke leže na jednom pravcu je klasika.
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
|
| [Vrh] |
|
|





