| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Unnamed One
Forumaš(ica)
Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)
Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 23:34 čet, 17. 11. 2005 Naslov: Re: diferencijabilnost |
    |
|
|
[quote="Unnamed One"]U skripti prof. Ungara iz analize 3 imamo slijedeći korolar (korolar 9.2.,
strana 88 );
F-ja f je klase C1 na svojoj domeni (koja je otvoren skup) ako i samo ako sve parcijalne derivacije od f postoje i neprekidne su na domeni od f.
[i]ako[/i] smjer mi je jasan, ali zašto vrijedi [i]samo ako[/i], tj. zašto f-ja koja je C1 mora imati neprekidne parcijalne derivacije :?:[/quote]
pa, sta nije to po definiciji tako?
imas fciju [latex]f:\Omega \subseteq R^n \longrightarrow R^m[/latex].
ako je ta fcija [latex]\in C^1[/latex] onda, po definiciji skupa [latex]C^1[/latex] znamo da je fcija neprekidna i da postoji diferencijal te fcije koji je isto tako neprekidan na cijelom [latex]\Omega[/latex] :-) mozda ovo i nije neko objasnjenje, a mozda sam i fulao negdje (iako mi se cini da nisam), ali sam barem pokusao to definirati :-)
neka me netko ispravi ako sam nesto krivo napravio u postupku ;-)
| Unnamed One (napisa): | U skripti prof. Ungara iz analize 3 imamo slijedeći korolar (korolar 9.2.,
strana 88 );
F-ja f je klase C1 na svojoj domeni (koja je otvoren skup) ako i samo ako sve parcijalne derivacije od f postoje i neprekidne su na domeni od f.
ako smjer mi je jasan, ali zašto vrijedi samo ako, tj. zašto f-ja koja je C1 mora imati neprekidne parcijalne derivacije  |
pa, sta nije to po definiciji tako?
imas fciju  .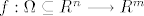
ako je ta fcija  onda, po definiciji skupa 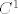 znamo da je fcija neprekidna i da postoji diferencijal te fcije koji je isto tako neprekidan na cijelom 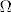  mozda ovo i nije neko objasnjenje, a mozda sam i fulao negdje (iako mi se cini da nisam), ali sam barem pokusao to definirati
neka me netko ispravi ako sam nesto krivo napravio u postupku 
|
|
| [Vrh] |
|
Ema
Forumaš(ica)
Pridružen/a: 01. 02. 2005. (12:44:59)
Postovi: (9C)16
|
| Postano: 0:28 pet, 18. 11. 2005 Naslov: |
|
|
|
jel to znaci da ako dokazemo da sve parcijalne derivacije neke f-je postoje i neprekidne su iz toga slijedi da je f klase c1,tj. da je i diferencijabilna pa ne moramo dokazivat da je lim kad (h,k)->
(0,0) od f(h,k)-f(0,0)-Df(0,0)[h k]=0?
jel to znaci da ako dokazemo da sve parcijalne derivacije neke f-je postoje i neprekidne su iz toga slijedi da je f klase c1,tj. da je i diferencijabilna pa ne moramo dokazivat da je lim kad (h,k)->
(0,0) od f(h,k)-f(0,0)-Df(0,0)[h k]=0?
|
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)
Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
|
| [Vrh] |
|
|
