| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
SMetesi
Gost
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 22:26 uto, 10. 1. 2006 Naslov: Postano: 22:26 uto, 10. 1. 2006 Naslov: |
    |
|
|
To je dosta netrivijalan problem za prvu godinu, pretpostavljam da je tvoj prijatelj sa fera barem druga. :D
U svakom slučaju, iracionalnost broja [latex]\sqrt{2}^{\sqrt{2}}[/latex]
slijedi iz tzv. [b]Gelfond-Schneidervog teorema[/b] koji u kratko kaže da je (kompleksni) broj oblika [latex]x^{y}[/latex] transcedentan (nije nultočka niti jednog netrivijalnog polinoma (dakle, isključen nulpolinom) s cjelobrojnim koeficijentima) ako je
[latex]x[/latex] algebarski (poništava ga neki netrivijalni polinom s cjelobrojnim koeficijentima, tj. nije transcedentan) i [latex]x \neq 0,1[/latex] i
ako je [latex]y[/latex] algebarski i iracionalan.
Kako je [latex]\sqrt{2}[/latex] algebarski i iracionalan, to je [latex]\sqrt{2}^{\sqrt{2}}[/latex] transcedentan, pa je specijalno i iracionalan
(svaki racionalni broj [latex]\frac{m}{n} \in \mathbb{Q}, \ m \in \mathbb{Z}, n \in \mathbb{N}[/latex] na trivijalan način možemo poništiti polinomom [latex]P[/latex] s cjelobrojnim kioeficijentima, npr. uzmemo [latex]P(x):=nx-m[/latex])
Ako ga zanima dokaz teorema neka se proba javiti nekome sa Seminara za teoriju brojeva i algebru da ga upute na literaturu:
http://web.math.hr/~duje/seminar.html
To je dosta netrivijalan problem za prvu godinu, pretpostavljam da je tvoj prijatelj sa fera barem druga. 
U svakom slučaju, iracionalnost broja 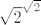
slijedi iz tzv. Gelfond-Schneidervog teorema koji u kratko kaže da je (kompleksni) broj oblika 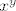 transcedentan (nije nultočka niti jednog netrivijalnog polinoma (dakle, isključen nulpolinom) s cjelobrojnim koeficijentima) ako je transcedentan (nije nultočka niti jednog netrivijalnog polinoma (dakle, isključen nulpolinom) s cjelobrojnim koeficijentima) ako je
 algebarski (poništava ga neki netrivijalni polinom s cjelobrojnim koeficijentima, tj. nije transcedentan) i algebarski (poništava ga neki netrivijalni polinom s cjelobrojnim koeficijentima, tj. nije transcedentan) i 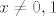 i i
ako je  algebarski i iracionalan. algebarski i iracionalan.
Kako je 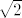 algebarski i iracionalan, to je algebarski i iracionalan, to je 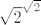 transcedentan, pa je specijalno i iracionalan transcedentan, pa je specijalno i iracionalan
(svaki racionalni broj 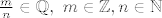 na trivijalan način možemo poništiti polinomom na trivijalan način možemo poništiti polinomom  s cjelobrojnim kioeficijentima, npr. uzmemo s cjelobrojnim kioeficijentima, npr. uzmemo 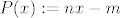 ) )
Ako ga zanima dokaz teorema neka se proba javiti nekome sa Seminara za teoriju brojeva i algebru da ga upute na literaturu:
http://web.math.hr/~duje/seminar.html
Zadnja promjena: Ilja; 1:10 sri, 11. 1. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 23:28 uto, 10. 1. 2006 Naslov: Postano: 23:28 uto, 10. 1. 2006 Naslov: |
    |
|
|
Dokaz Gelfond-Schneiderovog teorema se moze naci u knjigama
A. Baker: Transcendental Number Theory, Cambridge University Press, 1990,
Th. Schneider: Einfuhrung in die transzendenten Zahlen, Springer-Verlag, 1957,
a takodjer i u [url=http://www.iisc.ernet.in/nias/tn/tngst.htm]K. Ramachandra, Lectures on Transcendental Numbers[/url].
Dokaz Gelfond-Schneiderovog teorema se moze naci u knjigama
A. Baker: Transcendental Number Theory, Cambridge University Press, 1990,
Th. Schneider: Einfuhrung in die transzendenten Zahlen, Springer-Verlag, 1957,
a takodjer i u K. Ramachandra, Lectures on Transcendental Numbers.
|
|
| [Vrh] |
|
|





