| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 17:44 sri, 28. 9. 2005 Naslov: kako odrediti grešku?? |
    |
|
|
zad. Odrediti nepoznate koeficijente w1,w2,w3,w4 tako da formula integral (od 0 do 1) f(x)dx=w1f(-1)+w2f(1)+w3f'(-1)+w4f'(1)+R(f) ima max algebarski stupanj točnosti. Odredite algebarski stupanj točnosti i pogrešku R(f).
E sad, dobijem w1,=1 w2=1 w3=1/3 w4=-1/3
i dobijem da je formula egzaktna za polinome stupnja 3.
ali sad u formulu za grešku Rn(f) se ne uvrštava za n=3, nego za n=2.
Zašto???
I još jedno pitanje, kako znam kad u zadacima tog tipa koristim Gramm-Schmidtov postupak a kada ne??
zad. Odrediti nepoznate koeficijente w1,w2,w3,w4 tako da formula integral (od 0 do 1) f(x)dx=w1f(-1)+w2f(1)+w3f'(-1)+w4f'(1)+R(f) ima max algebarski stupanj točnosti. Odredite algebarski stupanj točnosti i pogrešku R(f).
E sad, dobijem w1,=1 w2=1 w3=1/3 w4=-1/3
i dobijem da je formula egzaktna za polinome stupnja 3.
ali sad u formulu za grešku Rn(f) se ne uvrštava za n=3, nego za n=2.
Zašto???
I još jedno pitanje, kako znam kad u zadacima tog tipa koristim Gramm-Schmidtov postupak a kada ne??
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)
Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
| Postano: 22:17 sri, 28. 9. 2005 Naslov: Re: kako odrediti grešku?? |
|
|
|
[quote="Anonymous"]zad. Odrediti nepoznate koeficijente w1,w2,w3,w4 tako da formula integral (od 0 do 1) f(x)dx=w1f(-1)+w2f(1)+w3f'(-1)+w4f'(1)+R(f) ima max algebarski stupanj točnosti. Odredite algebarski stupanj točnosti i pogrešku R(f).
E sad, dobijem w1,=1 w2=1 w3=1/3 w4=-1/3
i dobijem da je formula egzaktna za polinome stupnja 3.
ali sad u formulu za grešku Rn(f) se ne uvrštava za n=3, nego za n=2.
Zašto???
I još jedno pitanje, kako znam kad u zadacima tog tipa koristim Gramm-Schmidtov postupak a kada ne??[/quote]
Pitanje oko formule za pogrešku probajte malo reformulirati, jer ovako ne razumijem što pitate. :?
A odgovor na zadnje pitanje možete naći na
http://degiorgi.math.hr/forum/viewtopic.php?p=36165#36165
| Anonymous (napisa): | zad. Odrediti nepoznate koeficijente w1,w2,w3,w4 tako da formula integral (od 0 do 1) f(x)dx=w1f(-1)+w2f(1)+w3f'(-1)+w4f'(1)+R(f) ima max algebarski stupanj točnosti. Odredite algebarski stupanj točnosti i pogrešku R(f).
E sad, dobijem w1,=1 w2=1 w3=1/3 w4=-1/3
i dobijem da je formula egzaktna za polinome stupnja 3.
ali sad u formulu za grešku Rn(f) se ne uvrštava za n=3, nego za n=2.
Zašto???
I još jedno pitanje, kako znam kad u zadacima tog tipa koristim Gramm-Schmidtov postupak a kada ne?? |
Pitanje oko formule za pogrešku probajte malo reformulirati, jer ovako ne razumijem što pitate. 
A odgovor na zadnje pitanje možete naći na
http://degiorgi.math.hr/forum/viewtopic.php?p=36165#36165
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)
Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
| Postano: 22:47 sri, 28. 9. 2005 Naslov: |
|
|
|
[quote="Anonymous"]treba ocjeniti grešku, pa meni tu piše:
Rn(f)<= (n!)^4*(b-a)^(2n+1)*M2nf/((2n+1)*[(2n!)]^3) (koja je to formula????) i sad se tu kao uvrštava n=2...
jel to uopće dobro ili se to nekak drugačije rješava?[/quote]
Neće ići tako. Formula koju ste naveli je ocjena pogreške kod produljene Gauss-Legendreove integracije (G-L integracija je spec. slučaj Gaussove integracije kada je težinska funkcija w=1).
U vašem slučaju se ne radi o Gaussovoj integraciji, pa morate sami naći izraz za pogrešku, npr. koristeći razvoj funkcije f u Taylorov polinom stupnja 4 (npr. oko točke -1), naravno, uz pretpostavku da je f klase C^5.
Mislim da se sličan zadatak radio na vježbama pa tamo i pogledajte.
| Anonymous (napisa): | treba ocjeniti grešku, pa meni tu piše:
Rn(f)⇐ (n!)^4*(b-a)^(2n+1)*M2nf/((2n+1)*[(2n!)]^3) (koja je to formula????) i sad se tu kao uvrštava n=2...
jel to uopće dobro ili se to nekak drugačije rješava? |
Neće ići tako. Formula koju ste naveli je ocjena pogreške kod produljene Gauss-Legendreove integracije (G-L integracija je spec. slučaj Gaussove integracije kada je težinska funkcija w=1).
U vašem slučaju se ne radi o Gaussovoj integraciji, pa morate sami naći izraz za pogrešku, npr. koristeći razvoj funkcije f u Taylorov polinom stupnja 4 (npr. oko točke -1), naravno, uz pretpostavku da je f klase C^5.
Mislim da se sličan zadatak radio na vježbama pa tamo i pogledajte.
|
|
| [Vrh] |
|
beros
Forumaš(ica)
Pridružen/a: 06. 11. 2002. (11:48:22)
Postovi: (29)16
|
| Postano: 13:18 čet, 29. 9. 2005 Naslov: |
|
|
|
U ovom slučaju bi pogrešku trebalo ocjeniti pomoću razvoja funkcije u Taylorov red. Promatrate funkciju F(x) takvu da je f(x)=F'(x) i nju ćete razvijati. Priča kreće otprilike ovako
[latex] \int_a^b f(x) dx - ( w_1 f(a) + \cdots + w_4 f'(b))[/latex]
što je isto kao (iskoristimo definiciju funkcije F i Newton-Leibnitzovu formulu:
[latex] F(b)-F(a)- ( w_1 F'(a) + \cdots + w_4 F''(b))[/latex]
u ovoj formuli sada radimo razvoj funkcija F, F', F'' u Taylorov red oko neke točke (najčešće a ili b, a može i sredina intervala), nešto se poništi, a za pogrešku promatramo ponašanje prvog člana u redu koji ostaje.
Sjećanje me još uvijek dobro služi pa znam da sam ovakav zadatak rješio na vježbama i ove i prošle i pretprošle godine. Ali kada je lakše pisati poruku na forumu ... (Ovo je u skladu s onom: ... ako ništa ne pomaže, pročitaj upute.)
[color=darkblue]mod edit: podesio latex code[/color]
U ovom slučaju bi pogrešku trebalo ocjeniti pomoću razvoja funkcije u Taylorov red. Promatrate funkciju F(x) takvu da je f(x)=F'(x) i nju ćete razvijati. Priča kreće otprilike ovako
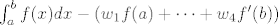
što je isto kao (iskoristimo definiciju funkcije F i Newton-Leibnitzovu formulu:
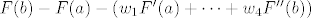
u ovoj formuli sada radimo razvoj funkcija F, F', F'' u Taylorov red oko neke točke (najčešće a ili b, a može i sredina intervala), nešto se poništi, a za pogrešku promatramo ponašanje prvog člana u redu koji ostaje.
Sjećanje me još uvijek dobro služi pa znam da sam ovakav zadatak rješio na vježbama i ove i prošle i pretprošle godine. Ali kada je lakše pisati poruku na forumu ... (Ovo je u skladu s onom: ... ako ništa ne pomaže, pročitaj upute.)
mod edit: podesio latex code
|
|
| [Vrh] |
|
Gost
|
| Postano: 14:15 pet, 30. 9. 2005 Naslov: |
|
|
|
da, da, znam da je napravljen zadatak na vježbama :miniklap:
ali, nama koji nismo dali ma3, (a ma2 tako davno da smo sve pozaboravljali) malo zapinje taj Taylorov polinom, pa ne bi škodilo napraviti još jedan primjer, npr. onaj u kojem nema h, ili onaj u kojem osim f(b), ima i f'(b), pa se sve ne pokrati , ili??? bilo bi to skroz lijepo od vas :D
da, da, znam da je napravljen zadatak na vježbama 
ali, nama koji nismo dali ma3, (a ma2 tako davno da smo sve pozaboravljali) malo zapinje taj Taylorov polinom, pa ne bi škodilo napraviti još jedan primjer, npr. onaj u kojem nema h, ili onaj u kojem osim f(b), ima i f'(b), pa se sve ne pokrati , ili??? bilo bi to skroz lijepo od vas 
|
|
| [Vrh] |
|
|
