|
[quote="Anonymous"]molim da mi neko objasni onaj teorem da su sve nultocke ortogonalnih polinoma realne,različite i elementi [a,b].
da li profesor Drmač pita i onaj zadnji dio s matricama?[/quote]
Označimo s
[latex]\langle f,g\rangle := \int_{a}^{b} w(x)f(x)g(x) dx [/latex]
pripadni skalarni produkt, pri čemu je [latex] w : [a,b] \rightarrow \mathbb{R}_{\geq 0}[/latex] ([latex]w \neq 0[/latex]) nenegativna neprekidna funkcija (težinska funkcija). Označimo s [latex]\{P_n\}_{n \in \mathbb{Z}_+}[/latex]
pripadnu familiju ortogonalnih polinoma, pri čemu je [latex]P_n[/latex]
stupnja [latex]n[/latex]. Tu familiju možemo dobiti klasičnim Gram-Schmidtovim postupkom ortogonalizacije kanonske baze [latex]\{1,x, x^2,\ldots \}[/latex] prostora polinoma [latex]\mathcal{P}[/latex], obzirom na gornji skalarni produkt. Bez narušavanja općenitosti možemo uzeti da su svi [latex]P_n [/latex] normirani (kao polinomi, tj. u smislu da im je vodeći koeficijent jednak [latex]1[/latex]), budući nam nije bitna ortonormiranost, već samo ortogonalnost (budući su ortogonalni polinomi jedinstveni do na ne-nul konstantu).
Umimo [latex]n \in \mathbb{N}[/latex]. Tvrdimo da [latex]P_n[/latex] ima barem jednu (realnu) nultočku i da se ona nalazi unutar segmenta [latex][a,b][/latex]. U protivnom bi bilo [latex]|P_n(x)|>0, \quad \forall x \in [a,b] [/latex] pa budući je
(po konstrukciji) [latex]P_n[/latex] okomit na [latex]P_0 =1[/latex], to je i [latex]|P_n|=sgn(P_n) \cdot P_n[/latex] okomit na [latex]P_0=1[/latex], tj.
[latex]0=\langle |P_n|, 1\rangle=\int_{a}^{b}w(x) |P_n(x)| \cdot 1 dx[/latex]
pa zbog pozitivnosti integrala, neprekidnosti i nenegativnosti funkcije [latex]x \mapsto w(x)|P_n(x)|[/latex] mora biti [latex]P_n(x)=0, \quad \forall x\in [a,b][/latex] što je kontradikcija s pretpostavkom [latex]|P_n(x)|>0, \quad \forall x \in [a,b] [/latex].
Označimo sada s [latex]x_1, \ldots, x_m [/latex] sve (međusobno različite) nultočke od [latex] P_n[/latex], [latex]1\leq m \leq n[/latex] iz [latex] [a,b][/latex]. Kada bi bilo [latex] m < n[/latex], onda bi polinom definiran sa [latex] R_{m+n}(x):=Q_m(x) \cdot P_n(x)[/latex], pri čemu je [latex] Q_m(x):= (x-x_1)\cdots (x-x_m)[/latex], bio stalnog predznaka na [latex][a,b] [/latex], no s druge strane, budući je [latex] P_n[/latex] okomit na sve polinome stupnja manjeg od [latex] n[/latex] (a polinom [latex] Q_m[/latex] je stupnja [latex] m<n [/latex] po pretpostavci), imamo
[latex]0= \langle P_n, Q_m\rangle=\int_{a}^{b}w(x)P_n(x)Q_m(x)dx= \int_{a}^{b}w(x)R_{m+n}(x)dx[/latex], pa zbog stalnog predznaka od [latex]R_{m+n}[/latex], nenegativnosti funkcije [latex]w[/latex] i pozitivnosti integrala nužno mora biti [latex]R_{m+n} =0[/latex], što je očito kontradikcija (stupanj polinoma [latex]R_{m+n}[/latex] je jednak [latex]m+n>0[/latex]). Zbog toga je [latex]m =n[/latex], dakle [latex]P_n[/latex] ima točno [latex]n[/latex] različitih nultočki (formalno gledajući mi smo dokazali da ih ima više ili jednako od [latex]n[/latex], a obrnuta nejednakost slijedi iz osnovnog teorema algebre) i sve su unutar segmenta [latex][a,b][/latex] za svako [latex]n \in \mathbb{N}[/latex].
| Anonymous (napisa): | molim da mi neko objasni onaj teorem da su sve nultocke ortogonalnih polinoma realne,različite i elementi [a,b].
da li profesor Drmač pita i onaj zadnji dio s matricama? |
Označimo s
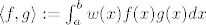
pripadni skalarni produkt, pri čemu je 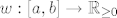 ( (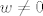 ) nenegativna neprekidna funkcija (težinska funkcija). Označimo s ) nenegativna neprekidna funkcija (težinska funkcija). Označimo s 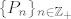
pripadnu familiju ortogonalnih polinoma, pri čemu je 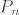
stupnja  . Tu familiju možemo dobiti klasičnim Gram-Schmidtovim postupkom ortogonalizacije kanonske baze . Tu familiju možemo dobiti klasičnim Gram-Schmidtovim postupkom ortogonalizacije kanonske baze 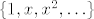 prostora polinoma prostora polinoma 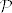 , obzirom na gornji skalarni produkt. Bez narušavanja općenitosti možemo uzeti da su svi , obzirom na gornji skalarni produkt. Bez narušavanja općenitosti možemo uzeti da su svi 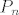 normirani (kao polinomi, tj. u smislu da im je vodeći koeficijent jednak normirani (kao polinomi, tj. u smislu da im je vodeći koeficijent jednak  ), budući nam nije bitna ortonormiranost, već samo ortogonalnost (budući su ortogonalni polinomi jedinstveni do na ne-nul konstantu). ), budući nam nije bitna ortonormiranost, već samo ortogonalnost (budući su ortogonalni polinomi jedinstveni do na ne-nul konstantu).
Umimo  . Tvrdimo da . Tvrdimo da 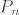 ima barem jednu (realnu) nultočku i da se ona nalazi unutar segmenta ima barem jednu (realnu) nultočku i da se ona nalazi unutar segmenta 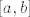 . U protivnom bi bilo . U protivnom bi bilo 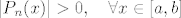 pa budući je pa budući je
(po konstrukciji) 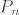 okomit na okomit na 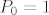 , to je i , to je i 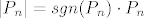 okomit na okomit na 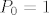 , tj. , tj.
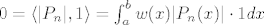
pa zbog pozitivnosti integrala, neprekidnosti i nenegativnosti funkcije 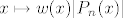 mora biti mora biti 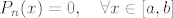 što je kontradikcija s pretpostavkom što je kontradikcija s pretpostavkom 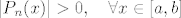 . .
Označimo sada s  sve (međusobno različite) nultočke od sve (međusobno različite) nultočke od 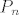 , , 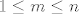 iz iz 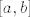 . Kada bi bilo . Kada bi bilo 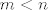 , onda bi polinom definiran sa , onda bi polinom definiran sa 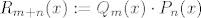 , pri čemu je , pri čemu je 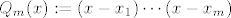 , bio stalnog predznaka na , bio stalnog predznaka na 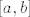 , no s druge strane, budući je , no s druge strane, budući je 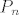 okomit na sve polinome stupnja manjeg od okomit na sve polinome stupnja manjeg od  (a polinom (a polinom 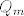 je stupnja je stupnja 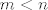 po pretpostavci), imamo po pretpostavci), imamo
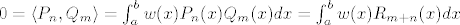 , pa zbog stalnog predznaka od , pa zbog stalnog predznaka od 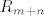 , nenegativnosti funkcije , nenegativnosti funkcije 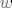 i pozitivnosti integrala nužno mora biti i pozitivnosti integrala nužno mora biti 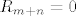 , što je očito kontradikcija (stupanj polinoma , što je očito kontradikcija (stupanj polinoma 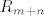 je jednak je jednak 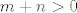 ). Zbog toga je ). Zbog toga je  , dakle , dakle 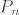 ima točno ima točno  različitih nultočki (formalno gledajući mi smo dokazali da ih ima više ili jednako od različitih nultočki (formalno gledajući mi smo dokazali da ih ima više ili jednako od  , a obrnuta nejednakost slijedi iz osnovnog teorema algebre) i sve su unutar segmenta , a obrnuta nejednakost slijedi iz osnovnog teorema algebre) i sve su unutar segmenta 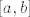 za svako za svako  . .
|




