| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
 Postano: 13:26 uto, 6. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine Postano: 13:26 uto, 6. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine |
    |
|
|
[quote="HijenA"]
dakle...treba naci prvi integral jednadzbe:
[latex]y'=\frac{3x-7y+2}{2x+5y-1}[/latex]
zahvaljujem :-D[/quote]
Ovako bez raspisivanja, čini mi se da prvo moraš pogledati da li je determinanta (3 -7),(2,5) različita od 0. Ovdje je, pa uvodiš supst. u=x-alfa,
v=y-beta. Alfa i beta izračunaš preko Cramera.
3alfa-7beta+2=0
2alfa+5beta-1=0. I onda se to svede na hom. jdbu.
| HijenA (napisa): |
dakle...treba naci prvi integral jednadzbe:
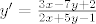
zahvaljujem  |
Ovako bez raspisivanja, čini mi se da prvo moraš pogledati da li je determinanta (3 -7),(2,5) različita od 0. Ovdje je, pa uvodiš supst. u=x-alfa,
v=y-beta. Alfa i beta izračunaš preko Cramera.
3alfa-7beta+2=0
2alfa+5beta-1=0. I onda se to svede na hom. jdbu.
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 13:32 uto, 6. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine Postano: 13:32 uto, 6. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine |
    |
|
|
[quote="Anđelčić"][quote="HijenA"]
dakle...treba naci prvi integral jednadzbe:
[latex]y'=\frac{3x-7y+2}{2x+5y-1}[/latex]
zahvaljujem :-D[/quote]
Ovako bez raspisivanja, čini mi se da prvo moraš pogledati da li je determinanta (3 -7),(2,5) različita od 0. Ovdje je, pa uvodiš supst. u=x-alfa,
v=y-beta. Alfa i beta izračunaš preko Cramera.
3alfa-7beta+2=0
2alfa+5beta-1=0. I onda se to svede na hom. jdbu.[/quote]
znaci...zapravo je oblik jednadzbi:
[latex]y'=\frac{u(x)}{v(x)}[/latex]
correct?
i onda je
[latex]u=x-\alpha[/latex]
[latex]v=y-\beta[/latex]
?
eh...da. i kako rijesiti zadatke kod kojih je determinanta jednaka 0?
| Anđelčić (napisa): | | HijenA (napisa): |
dakle...treba naci prvi integral jednadzbe:
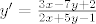
zahvaljujem  |
Ovako bez raspisivanja, čini mi se da prvo moraš pogledati da li je determinanta (3 -7),(2,5) različita od 0. Ovdje je, pa uvodiš supst. u=x-alfa,
v=y-beta. Alfa i beta izračunaš preko Cramera.
3alfa-7beta+2=0
2alfa+5beta-1=0. I onda se to svede na hom. jdbu. |
znaci...zapravo je oblik jednadzbi:
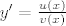
correct?
i onda je
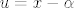
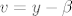
?
eh...da. i kako rijesiti zadatke kod kojih je determinanta jednaka 0?
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
Anđelčić
Forumaš(ica)

Pridružen/a: 11. 05. 2005. (16:57:50)
Postovi: (201)16
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:57 uto, 6. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine Postano: 19:57 uto, 6. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine |
    |
|
|
[quote="HijenA"]
znaci...zapravo je oblik jednadzbi:
[latex]y'=\frac{u(x)}{v(x)}[/latex]
correct?
i onda je
[latex]u=x-\alpha[/latex]
[latex]v=y-\beta[/latex]
?
[/quote]
Neeeeeeeee....
Znači ovako...Onaj dio sa determinantom i [latex]u=x-\alpha[/latex] [latex]v=y-\beta[/latex] je dobar.
Općenito, kada imaš jdn. oblika [latex]y'=\frac{ax+by+c}{a_1x+b_1y+c_1}[/latex]
Onda gledaš da li je determinanta
[code:1]
a b
a1 b1[/code:1]
jednaka ili različita nuli. (kako se piše determinanta u latexu?)
Ako je razlicita nuli, onda dalje ono sa alfa i beta..
Pa dalje imaš
[latex]\frac{dv}{du}=\frac{a+b\frac{v}{u}}{a_1+b_1\frac{v}{u}}[/latex]
ne uvrštavaš za u i v još ništa, sada rješavaš tu jednadžbu pomoću substitucije [latex]z=\frac{v}{u}[/latex], odnosno [latex]z'u+z=v'[/latex]
Dalje imaš da je [latex]z'u+z=\frac{a+bz}{a_1+b_1z}[/latex]
I sada to znaš rješiti ;)
[quote]
eh...da. i kako rijesiti zadatke kod kojih je determinanta jednaka 0?[/quote]
Kada je determinanta jednaka nuli, onda je u jednadžbi [latex]y'=\frac{ax+by+c}{a_1x+b_1y+c_1}[/latex]
nazivnik proporcionalan sa brojnikom, tj.
[latex]a_1x+b_1y=\lambda(ax+by)[/latex]
tada uvrštavaš substituciju z=ax+by, deriviraš dz/dx te tada dobiješ z'=a+by'
Izraziš y' i uvrstiš ga u početnu jednadžbu gdje ti sad brojnik izgleda z+c, a nazivnik [latex]\lambda[/latex]z+c1 i dalje znaš ;)
[quote="HijenA"]uh...maybe i'm stupid, ali nesto se cudno dogadja:
[latex]\int\frac {dy}{y\ln y}=\int\frac {dx}{\sin x}[/latex]
to dobijem kad rjesavam ovu ispravnu jednadzbu. e sad...posto se trazi prvi integral fcije, da li je ovo dovoljno? i ako sam opet nesto u procesu zeznuo, molim da se ispravi. secondly, da li se ovo moze nekako jednostavno integrirati ili se opet mora ici na parcijalne integracije?[/quote]
Moraš to izintegrirati ;)
U lijevom integralu imaš substituciju t=lny pa je dt=1/y*dy ;) a drugog imaš u tablicama :twisted: (bar ja imam :D ) i jednak je:
[latex]\ln{|{\tan{\frac{x}{2}}}|}[/latex]
| HijenA (napisa): |
znaci...zapravo je oblik jednadzbi:
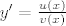
correct?
i onda je
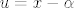
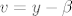
?
|
Neeeeeeeee....
Znači ovako...Onaj dio sa determinantom i 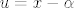 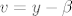 je dobar. je dobar.
Općenito, kada imaš jdn. oblika 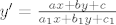
Onda gledaš da li je determinanta
jednaka ili različita nuli. (kako se piše determinanta u latexu?)
Ako je razlicita nuli, onda dalje ono sa alfa i beta..
Pa dalje imaš
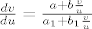
ne uvrštavaš za u i v još ništa, sada rješavaš tu jednadžbu pomoću substitucije  , odnosno , odnosno 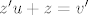
Dalje imaš da je 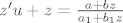
I sada to znaš rješiti 
| Citat: |
eh...da. i kako rijesiti zadatke kod kojih je determinanta jednaka 0? |
Kada je determinanta jednaka nuli, onda je u jednadžbi 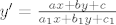
nazivnik proporcionalan sa brojnikom, tj.
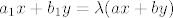
tada uvrštavaš substituciju z=ax+by, deriviraš dz/dx te tada dobiješ z'=a+by'
Izraziš y' i uvrstiš ga u početnu jednadžbu gdje ti sad brojnik izgleda z+c, a nazivnik  z+c1 i dalje znaš z+c1 i dalje znaš 
| HijenA (napisa): | uh...maybe i'm stupid, ali nesto se cudno dogadja:
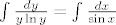
to dobijem kad rjesavam ovu ispravnu jednadzbu. e sad...posto se trazi prvi integral fcije, da li je ovo dovoljno? i ako sam opet nesto u procesu zeznuo, molim da se ispravi. secondly, da li se ovo moze nekako jednostavno integrirati ili se opet mora ici na parcijalne integracije? |
Moraš to izintegrirati 
U lijevom integralu imaš substituciju t=lny pa je dt=1/y*dy  a drugog imaš u tablicama a drugog imaš u tablicama  (bar ja imam (bar ja imam  ) i jednak je: ) i jednak je:
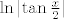
_________________
The Dude Abides
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 0:35 sri, 7. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine Postano: 0:35 sri, 7. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine |
    |
|
|
[quote="vili"][quote="Lord Sirius"]drugog imaš u tablicama :twisted: (bar ja imam :D ) i jednak je:
[latex]\ln{|{\tan{\frac{x}{2}}}|}[/latex][/quote]
Rješava se univerzalnom supstitucijom 8)[/quote]
Netko me pokudio, a kolki post sam napisao :cry: :cry: :lol:
Nego, nisam baš bio slušao na vježbama, ali čini mi se da je bilo spomenuto da se integrali moraju rješavati u smislu npr. lnx se mora integrirat parcijalnom integracijom, a ne samo prepisati s papira integral od lnx, tako da mogu očekivati da će mi se skidati bodovi ako 1/sinx ne integriram univerzalnom substitucijom ili sam krivo čuo nešta? :)
| vili (napisa): | | Lord Sirius (napisa): | drugog imaš u tablicama  (bar ja imam (bar ja imam  ) i jednak je: ) i jednak je:
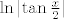 |
Rješava se univerzalnom supstitucijom  |
Netko me pokudio, a kolki post sam napisao   
Nego, nisam baš bio slušao na vježbama, ali čini mi se da je bilo spomenuto da se integrali moraju rješavati u smislu npr. lnx se mora integrirat parcijalnom integracijom, a ne samo prepisati s papira integral od lnx, tako da mogu očekivati da će mi se skidati bodovi ako 1/sinx ne integriram univerzalnom substitucijom ili sam krivo čuo nešta? 
_________________
The Dude Abides
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
filipnet
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: 
Lokacija: cvrsto na stolici
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:03 čet, 8. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine Postano: 19:03 čet, 8. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine |
    |
|
|
[quote="filipnet"]
ja imam jedno pitanje vezano za gornji zadatak. ja sam ga rjesavao i dobio fino i alfa i beta! uveo supstituciju z=v/u i na kraju dobio
(3-9z-5z^2)/(2+5z) tj. kad faktorizam ne dobim ciste nultocke, jesam ja to dobro rijesio?
dobijem z=(9+-141^(1/2))/10[/quote]
Meni tako isto ispada pa pretpostavljam da je dobro.
Možeš u prvu ruku jednu nultočku označiti sa a, a drugu sa b, pa onda dalje radiš tako.
Uglavnom, možeš ići sa a i b dok ne dođeš do momenta kada ćeš morati razlomak rastaviti na parcijalne razlomke, tada ćeš morati malo vremena potrošiti na računanje, ali tako i tako će ti ružni brojevi izaći iz integrala (jer su konstante) u idućem koraku.
| filipnet (napisa): |
ja imam jedno pitanje vezano za gornji zadatak. ja sam ga rjesavao i dobio fino i alfa i beta! uveo supstituciju z=v/u i na kraju dobio
(3-9z-5z^2)/(2+5z) tj. kad faktorizam ne dobim ciste nultocke, jesam ja to dobro rijesio?
dobijem z=(9+-141^(1/2))/10 |
Meni tako isto ispada pa pretpostavljam da je dobro.
Možeš u prvu ruku jednu nultočku označiti sa a, a drugu sa b, pa onda dalje radiš tako.
Uglavnom, možeš ići sa a i b dok ne dođeš do momenta kada ćeš morati razlomak rastaviti na parcijalne razlomke, tada ćeš morati malo vremena potrošiti na računanje, ali tako i tako će ti ružni brojevi izaći iz integrala (jer su konstante) u idućem koraku.
_________________
The Dude Abides
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 19:59 čet, 8. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine Postano: 19:59 čet, 8. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine |
    |
|
|
[quote="Lord Sirius"]Uglavnom, možeš ići sa a i b dok ne dođeš do momenta kada ćeš morati razlomak rastaviti na parcijalne razlomke, tada ćeš morati malo vremena potrošiti na računanje, ali tako i tako će ti ružni brojevi izaći iz integrala (jer su konstante) u idućem koraku.[/quote]
Stvarno se može tak?
Ne znam, nisam probao...
Već stvarno osjećam da moram svakom loncu bit poklopac (sorry@Lord Sirius) al za to sam se valjda javio :?
Enivej, alternativno riješenje:
Dobiješ na lijevoj strani za izračunat integral od
[latex]\frac{(2+5z)dz}{3-9z-5z^2}[/latex]
(sorry na polovičnim formulama, tek svladavam LateX :))
E sad, izlučiš minus i u jednom dijelu supstituiraš
[latex]t=5z^2+9z-3[/latex]
i izračunaš
[latex]dt=10z+9[/latex]
Sad razlomak pod integralom proširiš sa 2 i izlučiš 1/2 i ovih 10z+4 u brojniku napišeš kao 10z + 9 - 5 i odvojiš na 2 integrala u kojima u prvom imaš baš ono što trebaš da supstituiraš sa t, a u drugom nazivnik napišeš kao
[latex](\sqrt{5}z+\frac{9}{2\sqrt{5}})^2-\frac{141}{20}[/latex]
znači, želiš dobiti nazivnik oblika w^2-a^2 gdje je w varijabla a a konstanta(a brojnik dw). To je jedan od takoreći tabličnih integrala (dobili smo ga na papiru skupa sa osnovnima od asistenata na analizi 2) i onda napokon supstituiraš
[latex]w=\sqrt{5}z+\frac{9}{2\sqrt{5}}[/latex]
i središ to i integriraš.
Inače, stvarno mi nije jasno zašto su dali tako mučan zadatak na kolokviju al nadajmo se da će sutra biti bolje :figa2:
Ako nekom slučajno nije jasan dio postupka nek mi se javi na pm.
| Lord Sirius (napisa): | | Uglavnom, možeš ići sa a i b dok ne dođeš do momenta kada ćeš morati razlomak rastaviti na parcijalne razlomke, tada ćeš morati malo vremena potrošiti na računanje, ali tako i tako će ti ružni brojevi izaći iz integrala (jer su konstante) u idućem koraku. |
Stvarno se može tak?
Ne znam, nisam probao...
Već stvarno osjećam da moram svakom loncu bit poklopac (sorry@Lord Sirius) al za to sam se valjda javio 
Enivej, alternativno riješenje:
Dobiješ na lijevoj strani za izračunat integral od
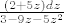
(sorry na polovičnim formulama, tek svladavam LateX  ) )
E sad, izlučiš minus i u jednom dijelu supstituiraš
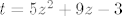
i izračunaš
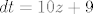
Sad razlomak pod integralom proširiš sa 2 i izlučiš 1/2 i ovih 10z+4 u brojniku napišeš kao 10z + 9 - 5 i odvojiš na 2 integrala u kojima u prvom imaš baš ono što trebaš da supstituiraš sa t, a u drugom nazivnik napišeš kao
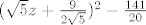
znači, želiš dobiti nazivnik oblika w^2-a^2 gdje je w varijabla a a konstanta(a brojnik dw). To je jedan od takoreći tabličnih integrala (dobili smo ga na papiru skupa sa osnovnima od asistenata na analizi 2) i onda napokon supstituiraš
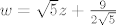
i središ to i integriraš.
Inače, stvarno mi nije jasno zašto su dali tako mučan zadatak na kolokviju al nadajmo se da će sutra biti bolje 
Ako nekom slučajno nije jasan dio postupka nek mi se javi na pm.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:23 čet, 8. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine Postano: 20:23 čet, 8. 12. 2005 Naslov: Re: ODJ - zadatak sa kolokvija od prosle godine |
    |
|
|
[quote="vili"][quote="Lord Sirius"]Uglavnom, možeš ići sa a i b dok ne dođeš do momenta kada ćeš morati razlomak rastaviti na parcijalne razlomke, tada ćeš morati malo vremena potrošiti na računanje, ali tako i tako će ti ružni brojevi izaći iz integrala (jer su konstante) u idućem koraku.[/quote]
Stvarno se može tak?
Ne znam, nisam probao...[/quote]
Pa evo kako sam ja to radio:
Kada se dođe do integrala
[latex]\int \frac{(2+5z)dz}{3-9z-5z^2}[/latex]
nultočke od razlomka su
[latex]a=\frac{-9+\sqrt{141}}{10}[/latex]
[latex]b=\frac{-9-\sqrt{141}}{10}[/latex]
Znači da onaj integral sada izgleda
[latex]\frac{2+5z}{(z-a)(z-b)}[/latex]
I rastav na parcijalne razlomke
[latex]\frac{A}{z-a}+\frac{B}{z-b}=\frac{A(z-b)+B(z-a)}{(z-a)(z-b)}=\frac{z(A+B)+(-Ab-Ba)}{(z-a)(z-b)}[/latex]
[latex]A+B=5[/latex]
[latex]A=5-B[/latex]
[latex]-Ab-aB=2[/latex]
[latex](B-5)b-aB=2[/latex]
[latex]B(b-a)=2-5b[/latex]
[latex]B=\frac{2+5b}{b-a}[/latex]
sada se uvrste a i b i dobije se B i A.
Kasnije imamo integral oblika
[latex]\int \frac{A}{z-a}+\int \frac{B}{z-b}=A\ln{(z-a)}+B\ln{(z-b)}[/latex]
A i jasno je da je taj integral mogao izgledati ovako:
[latex]\int \frac{5-\frac{2+5b}{b-a}}{z-a}+\int \frac{\frac{2+5b}{b-a}}{z-b}=(5-\frac{2+5b}{b-a})\ln{(z-a)}+\frac{2+5b}{b-a}\ln{(z-b)}[/latex]
IMO da sam ja asistent, ako bi netko dokraja dovršio zadatak gdje je nultočke substituirao sa a i b bez da ih je vraćao nazad, dao bih sve bodove. Ali ja nisam asistent pa koga briga :lol: :twisted:
[quote]
Već stvarno osjećam da moram svakom loncu bit poklopac (sorry@Lord Sirius) al za to sam se valjda javio :? [/quote]
To samo može biti dobro jer uvijek je bolje imati 2 razmišljanja o zadatku nego samo jedno ;) :)
| vili (napisa): | | Lord Sirius (napisa): | | Uglavnom, možeš ići sa a i b dok ne dođeš do momenta kada ćeš morati razlomak rastaviti na parcijalne razlomke, tada ćeš morati malo vremena potrošiti na računanje, ali tako i tako će ti ružni brojevi izaći iz integrala (jer su konstante) u idućem koraku. |
Stvarno se može tak?
Ne znam, nisam probao... |
Pa evo kako sam ja to radio:
Kada se dođe do integrala
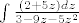
nultočke od razlomka su
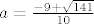
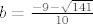
Znači da onaj integral sada izgleda
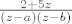
I rastav na parcijalne razlomke
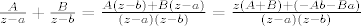
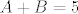
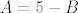
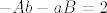
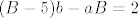
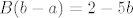
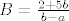
sada se uvrste a i b i dobije se B i A.
Kasnije imamo integral oblika
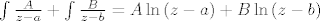
A i jasno je da je taj integral mogao izgledati ovako:
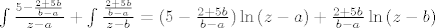
IMO da sam ja asistent, ako bi netko dokraja dovršio zadatak gdje je nultočke substituirao sa a i b bez da ih je vraćao nazad, dao bih sve bodove. Ali ja nisam asistent pa koga briga  
| Citat: |
Već stvarno osjećam da moram svakom loncu bit poklopac (sorry@Lord Sirius) al za to sam se valjda javio  |
To samo može biti dobro jer uvijek je bolje imati 2 razmišljanja o zadatku nego samo jedno  
_________________
The Dude Abides
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
|





















