| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vrag
Gost
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 15:42 ned, 18. 12. 2005 Naslov: Re: zadatak sa šahovskom pločom |
    |
|
|
[quote="Vrag"]Na beskonačno veliku šahovsku ploču bacamo novčić. Veličina kvadrata na šahovskoj ploči je a, a radijus novčića je manji od a/2.
a) Kolika je vjerojatnost da je novčić pao unutar jednog polja?
b) Koliko je vjerojatnost da je novčić pao tako da sječe točno jednu stranicu kvadrata?
a sam rješio, valjda... naime tu sam dobio 1/9 omjerom površina
b nikako ne znam na koji način riješiti jer kada sam krenuo omjerom površina dobio sam da se sve krati i dobivam 0[/quote]
Malo mi je cudno da ti rjesenje ne ovisi o radijusu novcica... :?
Trebas naci gdje sve smije pasti srediste novcica. 8) Ako je radijus novcica r, onda u zadatku a) srediste novcica smije pasti bilo gdje u kvadratu sa centrom u "velikom kvadraticu", stranice [latex]a-r[/latex]. 8) Dakle, vjerojatnost je [latex]\frac{(a-r)^2}{a^2}=\left(1-\frac{r}{a}\right)^2[/latex] :)
Slicno, u drugom zadatku, centar kruznice smije upasti svugdje osim u kvadraticima koji se nalaze u rubovima "velikog kvadratica" i imaju stranicu [latex]r[/latex]. :D Dakle, vjerojatnost koju trazis je [latex]\frac{a^2 - 4r^2}{a^2}=1 - \left(2\frac{r}{a}\right)^2[/latex]. 8)
[b]Uobicajni disklejmer:[/b] ja nisam "doma" s vjerojatnostima, pa oprezno s ovim rjesenjima... ;)
| Vrag (napisa): | Na beskonačno veliku šahovsku ploču bacamo novčić. Veličina kvadrata na šahovskoj ploči je a, a radijus novčića je manji od a/2.
a) Kolika je vjerojatnost da je novčić pao unutar jednog polja?
b) Koliko je vjerojatnost da je novčić pao tako da sječe točno jednu stranicu kvadrata?
a sam rješio, valjda... naime tu sam dobio 1/9 omjerom površina
b nikako ne znam na koji način riješiti jer kada sam krenuo omjerom površina dobio sam da se sve krati i dobivam 0 |
Malo mi je cudno da ti rjesenje ne ovisi o radijusu novcica... 
Trebas naci gdje sve smije pasti srediste novcica.  Ako je radijus novcica r, onda u zadatku a) srediste novcica smije pasti bilo gdje u kvadratu sa centrom u "velikom kvadraticu", stranice  . Dakle, vjerojatnost je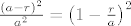  
Slicno, u drugom zadatku, centar kruznice smije upasti svugdje osim u kvadraticima koji se nalaze u rubovima "velikog kvadratica" i imaju stranicu  .  Dakle, vjerojatnost koju trazis je  .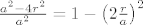
Uobicajni disklejmer: ja nisam "doma" s vjerojatnostima, pa oprezno s ovim rjesenjima... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Grga
Forumaš(ica)
Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
| Postano: 15:46 ned, 18. 12. 2005 Naslov: Re: zadatak sa šahovskom pločom |
|
|
|
[quote="Vrag"]Na beskonačno veliku šahovsku ploču bacamo novčić. Veličina kvadrata na šahovskoj ploči je a, a radijus novčića je manji od a/2.
a)
Kolika je vjerojatnost da je novčić pao unutar jednog polja?
b)
Koliko je vjerojatnost da je novčić pao tako da sječe točno jednu stranicu kvadrata?
a sam rješio, valjda... naime tu sam dobio 1/9 omjerom površina
b nikako ne znam na koji način riješiti jer kada sam krenuo omjerom površina dobio sam da se sve krati i dobivam 0
puno hvala svima koji probaj riješiti zadatak[/quote]
Gledamo gdje pada srediste novcica. Gdje god pao novcic, njegovo srediste se nalazi unutar jednog polja: ako u doljni lijevi ugao tog polja postavimo ishodiste koordinatnog sustava, prostor el. dogadaja nam je [latex]\Omega = \{(x,y):0\leq x,y \leq a\}[/latex].
Nas dogadaj A = {novcic je u potpunosti unutar polja} dogada se ako je srediste novcica udaljeno za vise od r od svakog od rubova polja, tj [latex]A=\{(x,y)):r\leq x,y \leq a-r\}[/latex].
[latex]P(A) = \frac{m(A)}{m(\Omega)} = \frac{((a-r)-r)^2}{a^2} = \frac{(a - 2r)^2}{a^2}[/latex]
Dogadaj B = {novcic sijece tocno jednu stranicu kvadrata}, tj srediste novcica je udaljeno za manje od r od jedne stranice kvadrata, ali od ostale tri je udaljen za vise od r, tj B je unija cetiri disjunktna dogadaja, po jedan za svaku stranicu kvadrata , npr za lijevu stranicu je [latex]B_l=\{(x,y)): 0 \leq x \leq r, r < y < a-r\}[/latex].
Mjera svakog od ta cetiri dogadaja je jednaka, pa imamo:
[latex]P(B) = \frac{m(B)}{m(\Omega)} = \frac{(4m(B_l))}{a^2} = \frac{4r((a-r)-r)}{a^2} = \frac{4r(a-2r)}{a^2}[/latex]
Moguce da sam negdje fulao, ali cini mi se kao da je dobro :D
| Vrag (napisa): | Na beskonačno veliku šahovsku ploču bacamo novčić. Veličina kvadrata na šahovskoj ploči je a, a radijus novčića je manji od a/2.
a)
Kolika je vjerojatnost da je novčić pao unutar jednog polja?
b)
Koliko je vjerojatnost da je novčić pao tako da sječe točno jednu stranicu kvadrata?
a sam rješio, valjda... naime tu sam dobio 1/9 omjerom površina
b nikako ne znam na koji način riješiti jer kada sam krenuo omjerom površina dobio sam da se sve krati i dobivam 0
puno hvala svima koji probaj riješiti zadatak |
Gledamo gdje pada srediste novcica. Gdje god pao novcic, njegovo srediste se nalazi unutar jednog polja: ako u doljni lijevi ugao tog polja postavimo ishodiste koordinatnog sustava, prostor el. dogadaja nam je  .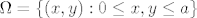
Nas dogadaj A = {novcic je u potpunosti unutar polja} dogada se ako je srediste novcica udaljeno za vise od r od svakog od rubova polja, tj  .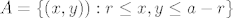
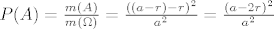
Dogadaj B = {novcic sijece tocno jednu stranicu kvadrata}, tj srediste novcica je udaljeno za manje od r od jedne stranice kvadrata, ali od ostale tri je udaljen za vise od r, tj B je unija cetiri disjunktna dogadaja, po jedan za svaku stranicu kvadrata , npr za lijevu stranicu je  .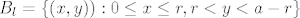
Mjera svakog od ta cetiri dogadaja je jednaka, pa imamo:
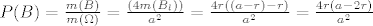
Moguce da sam negdje fulao, ali cini mi se kao da je dobro
_________________
Bri
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol:
Lokacija: /sbin/init
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)
Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
|
U prvom je obicni tip-feller, ali drugog sam stvarno zeznuo: ono moje je vjerojatnost da sijece 
