| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 3:07 sub, 24. 12. 2005 Naslov: prazna domena Postano: 3:07 sub, 24. 12. 2005 Naslov: prazna domena |
    |
|
|
ok...posto nemam pojma gdje bi ovo pitanje strpao, stavljam tu, pa ce modovi preselit ako nije dobro.
naime...raspravljajuci sa jednim kolegom (koji je ocigledno zavrsio matematiku, i to teorijskog tipa cini mi se) na usenet grupi hr.sci.matematika, skrenuta mi je paznja na meni potpuno nepoznat pojam. odnosno, to sto ta osoba tvrdi meni je vrlo cudno i, u neku ruku, neprihvatljivo (vjerojatno na to utjece moje ograniceno matematicko razmisljanje :gg:).
dakle...pojam se zove "prazna domena". kako smo dosli do takvog pojma? pa, zapravo, trebalo je izreci definiciju fcije. i sad...imamo dva [b]neprazna[/b] skupa A i B i preslikavanje sa jednog u drugo. to preslikavanje se zove fcija ako [latex]\forall a\in A[/latex] pridruzuje tocno jedan [latex]b \in B[/latex]. i, to je sve u redu. fcija, kao takva, je definirana.
medjutim...mene sad muci jedna druga stvar. taj kolega sa usenet grupe se protivi takvom nacinu definicije jer:
a) nije matematicki formalizam (sto je preslikavanje, recimo...no to i nije ttoliko bitno)
b) zasto se ogranicavati sa time da su A i B neprazni?
ovo drugo je puno zanimljivije.
naime, sto se dogadja kad je bilo koji od ta dva skupa prazan? ako je prazna domena fcije (odnosno skup A), onda nemamo pocetne elemente koje fcija preslikava (ili pridruzuje) elementima iz B. onda imamo dva slucaja: ili je takvoj domeni pridruzen prazan skup ili je pridruzen cijeli skup B. u prvom slucaju tvrdnja (barem sto se tice fcije) ispravna, no nema bas nekog smisla. u drugom slucaju, nistavilu (jer je skup A prazan) nije pridruzen jedan element iz B, vec su pridruzeni svi elementi iz B, ali to onda nije vise fcija. eventualno moze biti neki tip relacije, ali jos uvijek mi nije jasno kako nistavilo moze biti u relaciji sa nekim elementom. to nema nikakvog smisla.
ajmo sad pogledati kakva je situacija sa kodomenom. ako je kodomena prazna, onda opet postoje 2 slucaja: ili je domena prazan skup i u tom slucaju to preslikavanje stvarno jest fcija (jer se nistavilo preslikava u nistavilo), no to opet nema bas nekakvog smisla (a i trivijalno se vidi). no, u drugom slucaju imamo sve elemente iz domene koji se preslikavaju u nistavilo, dakle u jedan element. to isto jest fcija (po gornjoj definiciji, bitno je samo da se isti element iz A ne preslikava u dva razlicita elementa iz B). no, ni to matematicki nema smisla. jedinih primjera fcija kojih se ja mogu sjetit da nesto slicno rade su nul-fcije, nul-operatori i slicno, no i one preslikavaju u nesto sto nije nistavilo, konkretno, preslikavaju u 0.
eh sad...meni sad tu nije jasno zasto bi se definicija fcije uopce prosirivala na prazan skup ako to ocigledno nema smisla? neka mi netko to objasni i, po mogucnosti, da primjer takve fcije.
druga stvar je pitanje "sto je to fcija uopce?". naime, taj isti korisnik tvrdi [i]a priori[/i] da je fcija skup. ja se s time ne mogu uopce slozit, jer mislim da takva analogija ne vrijedi. zasto to mislim? prvenstveno zbog toga sto je fcija zapravo svojstvo koje odredjuje odnos izmedju dva skupa. primjerice, imamo fciju [latex] f:R->R: f(x)=x+1[/latex]. ta fcija tvori nekakav graf, a opisuje preslikavanje realnih brojeva iz R u R. dakle, ima svojstvo da pridruzuje, primjerice, broju 0 broj 1. takav uredjen par brojeva (0,1) (primjerice) zove se tocka. takvih tocaka na grafu ima beskonacno mnogo, ali oni nisu elementi fcije vec elementi grafa kojeg ta fcija tvori. dakle, fcija samo opisuje nastanak tog grafa, ne i sam graf.
eh...sad. mene interesira sta je od svega ovoga nadrobljenog u ovom ogromnom postu sa moje strane tocno i gdje grijesim.
hvala.
EDIT: zaboravih napomenuti: doticni kolega sa te news grupe konstatira da se tu ne moze koristiti gornja definicija fcije vec da se mora posegnuti za cistim matematickim formalizmom. buduci da ja ne znam drugaciju definiciju fcije od one gore, neka me netko i na tom podrucju prosvjetli :-)
ok...posto nemam pojma gdje bi ovo pitanje strpao, stavljam tu, pa ce modovi preselit ako nije dobro.
naime...raspravljajuci sa jednim kolegom (koji je ocigledno zavrsio matematiku, i to teorijskog tipa cini mi se) na usenet grupi hr.sci.matematika, skrenuta mi je paznja na meni potpuno nepoznat pojam. odnosno, to sto ta osoba tvrdi meni je vrlo cudno i, u neku ruku, neprihvatljivo (vjerojatno na to utjece moje ograniceno matematicko razmisljanje  ). ).
dakle...pojam se zove "prazna domena". kako smo dosli do takvog pojma? pa, zapravo, trebalo je izreci definiciju fcije. i sad...imamo dva neprazna skupa A i B i preslikavanje sa jednog u drugo. to preslikavanje se zove fcija ako 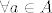 pridruzuje tocno jedan pridruzuje tocno jedan 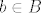 . i, to je sve u redu. fcija, kao takva, je definirana. . i, to je sve u redu. fcija, kao takva, je definirana.
medjutim...mene sad muci jedna druga stvar. taj kolega sa usenet grupe se protivi takvom nacinu definicije jer:
a) nije matematicki formalizam (sto je preslikavanje, recimo...no to i nije ttoliko bitno)
b) zasto se ogranicavati sa time da su A i B neprazni?
ovo drugo je puno zanimljivije.
naime, sto se dogadja kad je bilo koji od ta dva skupa prazan? ako je prazna domena fcije (odnosno skup A), onda nemamo pocetne elemente koje fcija preslikava (ili pridruzuje) elementima iz B. onda imamo dva slucaja: ili je takvoj domeni pridruzen prazan skup ili je pridruzen cijeli skup B. u prvom slucaju tvrdnja (barem sto se tice fcije) ispravna, no nema bas nekog smisla. u drugom slucaju, nistavilu (jer je skup A prazan) nije pridruzen jedan element iz B, vec su pridruzeni svi elementi iz B, ali to onda nije vise fcija. eventualno moze biti neki tip relacije, ali jos uvijek mi nije jasno kako nistavilo moze biti u relaciji sa nekim elementom. to nema nikakvog smisla.
ajmo sad pogledati kakva je situacija sa kodomenom. ako je kodomena prazna, onda opet postoje 2 slucaja: ili je domena prazan skup i u tom slucaju to preslikavanje stvarno jest fcija (jer se nistavilo preslikava u nistavilo), no to opet nema bas nekakvog smisla (a i trivijalno se vidi). no, u drugom slucaju imamo sve elemente iz domene koji se preslikavaju u nistavilo, dakle u jedan element. to isto jest fcija (po gornjoj definiciji, bitno je samo da se isti element iz A ne preslikava u dva razlicita elementa iz B). no, ni to matematicki nema smisla. jedinih primjera fcija kojih se ja mogu sjetit da nesto slicno rade su nul-fcije, nul-operatori i slicno, no i one preslikavaju u nesto sto nije nistavilo, konkretno, preslikavaju u 0.
eh sad...meni sad tu nije jasno zasto bi se definicija fcije uopce prosirivala na prazan skup ako to ocigledno nema smisla? neka mi netko to objasni i, po mogucnosti, da primjer takve fcije.
druga stvar je pitanje "sto je to fcija uopce?". naime, taj isti korisnik tvrdi a priori da je fcija skup. ja se s time ne mogu uopce slozit, jer mislim da takva analogija ne vrijedi. zasto to mislim? prvenstveno zbog toga sto je fcija zapravo svojstvo koje odredjuje odnos izmedju dva skupa. primjerice, imamo fciju 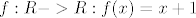 . ta fcija tvori nekakav graf, a opisuje preslikavanje realnih brojeva iz R u R. dakle, ima svojstvo da pridruzuje, primjerice, broju 0 broj 1. takav uredjen par brojeva (0,1) (primjerice) zove se tocka. takvih tocaka na grafu ima beskonacno mnogo, ali oni nisu elementi fcije vec elementi grafa kojeg ta fcija tvori. dakle, fcija samo opisuje nastanak tog grafa, ne i sam graf. . ta fcija tvori nekakav graf, a opisuje preslikavanje realnih brojeva iz R u R. dakle, ima svojstvo da pridruzuje, primjerice, broju 0 broj 1. takav uredjen par brojeva (0,1) (primjerice) zove se tocka. takvih tocaka na grafu ima beskonacno mnogo, ali oni nisu elementi fcije vec elementi grafa kojeg ta fcija tvori. dakle, fcija samo opisuje nastanak tog grafa, ne i sam graf.
eh...sad. mene interesira sta je od svega ovoga nadrobljenog u ovom ogromnom postu sa moje strane tocno i gdje grijesim.
hvala.
EDIT: zaboravih napomenuti: doticni kolega sa te news grupe konstatira da se tu ne moze koristiti gornja definicija fcije vec da se mora posegnuti za cistim matematickim formalizmom. buduci da ja ne znam drugaciju definiciju fcije od one gore, neka me netko i na tom podrucju prosvjetli 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 3:41 sub, 24. 12. 2005 Naslov: Postano: 3:41 sub, 24. 12. 2005 Naslov: |
    |
|
|
Nadam se da ce ti pametniji od mene lamentirali, pa cu samo kratko:
1. Kodomena prazna, domena neprazna :arrow: nemoguce. :? Neka je [i]x[/i] iz domene (postoji, jer je ona neprazna); koja bi bila slika od [i]x[/i]? :-k
2. Funkcija je relacija, a relacija je skup uredjenih parova, dakle i sama funkcija je (jako specifican) skup. 8) Iz te definicije (relacija koja za svaki [i]x0[/i] iz domene ima tocno jedan element ([i]x[/i], [i]y[/i]) takav da je [i]x[/i] = [i]x0[/i]) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene. 8)
Inace, povlacenje analogije funkcije i njenog grafa je opasno i treba izvoditi oprezno. :-s Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije. :shock: Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid. 8) Primjere nadji sam. O:)
Nadam se da ce ti pametniji od mene lamentirali, pa cu samo kratko:
1. Kodomena prazna, domena neprazna  nemoguce. nemoguce.  Neka je x iz domene (postoji, jer je ona neprazna); koja bi bila slika od x? Neka je x iz domene (postoji, jer je ona neprazna); koja bi bila slika od x? 
2. Funkcija je relacija, a relacija je skup uredjenih parova, dakle i sama funkcija je (jako specifican) skup.  Iz te definicije (relacija koja za svaki x0 iz domene ima tocno jedan element (x, y) takav da je x = x0) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene. Iz te definicije (relacija koja za svaki x0 iz domene ima tocno jedan element (x, y) takav da je x = x0) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene. 
Inace, povlacenje analogije funkcije i njenog grafa je opasno i treba izvoditi oprezno.  Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije. Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije.  Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid. Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid.  Primjere nadji sam. Primjere nadji sam. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 10:40 sub, 24. 12. 2005 Naslov: Postano: 10:40 sub, 24. 12. 2005 Naslov: |
    |
|
|
[quote="vsego"]Nadam se da ce ti pametniji od mene lamentirali, pa cu samo kratko:
1. Kodomena prazna, domena neprazna :arrow: nemoguce. :? Neka je [i]x[/i] iz domene (postoji, jer je ona neprazna); koja bi bila slika od [i]x[/i]? :-k[/quote]
to i mene interesira. eventualno bi moglo stajati da je slika od x nista, sto nema nikakvog smisla. niti bi matematicki bilo ikako upotrebljivo.
[quote]
2. Funkcija je relacija, a relacija je skup uredjenih parova, dakle i sama funkcija je (jako specifican) skup. 8) Iz te definicije (relacija koja za svaki [i]x0[/i] iz domene ima tocno jedan element ([i]x[/i], [i]y[/i]) takav da je [i]x[/i] = [i]x0[/i]) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene. 8)[/quote]
ali, opet, moras pretpostaviti da su dva skupa jednaka. ne moze neki skup sa n elemenata biti u relaciji sa praznim skupom. isto tako, prazan skup ne moze biti u relaciji sa nekim skupom elemenata. naravno, govorimo o uredjenim parovima koje ta relacija formira. no, opet govorimo o svojstvu, dakle, na koji nacin uparit 2 elementa, npr. dok sva takva "svojstvena" uparivanja cine skup svih uparivanja. zasto se na relaciju i fciju ne moze gledat kao svojstvo?
[quote]
Inace, povlacenje analogije funkcije i njenog grafa je opasno i treba izvoditi oprezno. :-s Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije. :shock: Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid. 8) Primjere nadji sam. O:)[/quote]
dobro...tu se slazem. zato sam i koristio ovaj vrlo jednostavan primjer (f(x)=x+1, za koju je trivijalno pokazati da je neprekidna na cijeloj domeni).
| vsego (napisa): | Nadam se da ce ti pametniji od mene lamentirali, pa cu samo kratko:
1. Kodomena prazna, domena neprazna  nemoguce. nemoguce.  Neka je x iz domene (postoji, jer je ona neprazna); koja bi bila slika od x? Neka je x iz domene (postoji, jer je ona neprazna); koja bi bila slika od x?  |
to i mene interesira. eventualno bi moglo stajati da je slika od x nista, sto nema nikakvog smisla. niti bi matematicki bilo ikako upotrebljivo.
| Citat: |
2. Funkcija je relacija, a relacija je skup uredjenih parova, dakle i sama funkcija je (jako specifican) skup.  Iz te definicije (relacija koja za svaki x0 iz domene ima tocno jedan element (x, y) takav da je x = x0) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene. Iz te definicije (relacija koja za svaki x0 iz domene ima tocno jedan element (x, y) takav da je x = x0) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene.  |
ali, opet, moras pretpostaviti da su dva skupa jednaka. ne moze neki skup sa n elemenata biti u relaciji sa praznim skupom. isto tako, prazan skup ne moze biti u relaciji sa nekim skupom elemenata. naravno, govorimo o uredjenim parovima koje ta relacija formira. no, opet govorimo o svojstvu, dakle, na koji nacin uparit 2 elementa, npr. dok sva takva "svojstvena" uparivanja cine skup svih uparivanja. zasto se na relaciju i fciju ne moze gledat kao svojstvo?
| Citat: |
Inace, povlacenje analogije funkcije i njenog grafa je opasno i treba izvoditi oprezno.  Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije. Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije.  Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid. Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid.  Primjere nadji sam. Primjere nadji sam.  |
dobro...tu se slazem. zato sam i koristio ovaj vrlo jednostavan primjer (f(x)=x+1, za koju je trivijalno pokazati da je neprekidna na cijeloj domeni).
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 11:22 sub, 24. 12. 2005 Naslov: Postano: 11:22 sub, 24. 12. 2005 Naslov: |
    |
|
|
Ako ti je domena prazna, onda sve stima, i slika funkcije je prazan skup, jer za svaki element iz slike vrijedi da postoji element iz domene koji se preslikava u njega.
Ako ti je kodomena prazna, mora biti i domena, jer se svaki element iz domene mora preslikavati u neki element iz kodomene.
Ako ti je domena prazna, onda sve stima, i slika funkcije je prazan skup, jer za svaki element iz slike vrijedi da postoji element iz domene koji se preslikava u njega.
Ako ti je kodomena prazna, mora biti i domena, jer se svaki element iz domene mora preslikavati u neki element iz kodomene.
_________________
Bri
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 11:47 sub, 24. 12. 2005 Naslov: Postano: 11:47 sub, 24. 12. 2005 Naslov: |
    |
|
|
[quote="Grga"]Ako ti je domena prazna, onda sve stima, i slika funkcije je prazan skup, jer za svaki element iz slike vrijedi da postoji element iz domene koji se preslikava u njega.
Ako ti je kodomena prazna, mora biti i domena, jer se svaki element iz domene mora preslikavati u neki element iz kodomene.[/quote]
pa to sam ja pokazao gore u svojem prvom postu. no, to ne odgovara na pitanje da li je takva definicija uopce potrebna i gdje bi se mogla upotrebljavati.
| Grga (napisa): | Ako ti je domena prazna, onda sve stima, i slika funkcije je prazan skup, jer za svaki element iz slike vrijedi da postoji element iz domene koji se preslikava u njega.
Ako ti je kodomena prazna, mora biti i domena, jer se svaki element iz domene mora preslikavati u neki element iz kodomene. |
pa to sam ja pokazao gore u svojem prvom postu. no, to ne odgovara na pitanje da li je takva definicija uopce potrebna i gdje bi se mogla upotrebljavati.
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 12:04 sub, 24. 12. 2005 Naslov: Postano: 12:04 sub, 24. 12. 2005 Naslov: |
    |
|
|
Zbunilo me to sto si ti gore pricao o slucaju da je "nistavilu" pridruzen cijeli skup. No sto je "nistavilo"? Nije problem u tome sto ti "nistavilu" pridruzujes vise od jednog elementa, jer ti tu pricas o "nistavilu" kao da je ono element praznog skupa, nego u tome da uopce nemas elemenata u domeni. Normalno da slika mora biti prazan skup ako nemas nijedan element u domeni, i taj slucaj uopce nema smisla.
A sad je li to potrebno i upotrebljava li se negdje iskreno nemam pojma, ali ne cini mi se bas kao da bi se igdje moglo koristiti. Vise mi se cini da se taj kolega "pravio vazan" pokazujuci ti da si "u krivu", nego da ti je ukazao na neku vaznu cinjenicu.
Zbunilo me to sto si ti gore pricao o slucaju da je "nistavilu" pridruzen cijeli skup. No sto je "nistavilo"? Nije problem u tome sto ti "nistavilu" pridruzujes vise od jednog elementa, jer ti tu pricas o "nistavilu" kao da je ono element praznog skupa, nego u tome da uopce nemas elemenata u domeni. Normalno da slika mora biti prazan skup ako nemas nijedan element u domeni, i taj slucaj uopce nema smisla.
A sad je li to potrebno i upotrebljava li se negdje iskreno nemam pojma, ali ne cini mi se bas kao da bi se igdje moglo koristiti. Vise mi se cini da se taj kolega "pravio vazan" pokazujuci ti da si "u krivu", nego da ti je ukazao na neku vaznu cinjenicu.
_________________
Bri
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 13:25 sub, 24. 12. 2005 Naslov: Postano: 13:25 sub, 24. 12. 2005 Naslov: |
    |
|
|
[quote="HijenA"][quote="vsego"]1. Kodomena prazna, domena neprazna :arrow: nemoguce. :? Neka je [i]x[/i] iz domene (postoji, jer je ona neprazna); koja bi bila slika od [i]x[/i]? :-k[/quote]
to i mene interesira. eventualno bi moglo stajati da je slika od x nista, sto nema nikakvog smisla. niti bi matematicki bilo ikako upotrebljivo.[/quote]
Ne moze biti "nista". :? Ako imas konkretan [i]x[/i], slika mu mora biti jednoznacno odredjena (pricamo o funkciji, ne?). :)
[quote="HijenA"][quote="vsego"]2. Funkcija je relacija, a relacija je skup uredjenih parova, dakle i sama funkcija je (jako specifican) skup. 8) Iz te definicije (relacija koja za svaki [i]x0[/i] iz domene ima tocno jedan element ([i]x[/i], [i]y[/i]) takav da je [i]x[/i] = [i]x0[/i]) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene. 8)[/quote]
ali, opet, moras pretpostaviti da su dva skupa jednaka.[/quote]
Huh? :grebgreb:
[quote="HijenA"]ne moze neki skup sa n elemenata biti u relaciji sa praznim skupom.[/quote]
Moze biti u praznoj relaciji, no onda to nije funkcija. 8)
[quote="HijenA"]isto tako, prazan skup ne moze biti u relaciji sa nekim skupom elemenata.[/quote]
Zasto ne? :grebgreb:
A = O // prazan skup
B = {1,2,...,n}
R subset AxB = O
Ovo mozemo smatrati funkcijom jer svakom elementu domene pridruzuje tocno jedan element kodomene. :shock: Ako mi ne vjerujes, potrazi protuprimjer. :P
Na praznim skupovima vrijede razna cuda... ;) Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17. :gg:
[quote="HijenA"][quote="vsego"]Inace, povlacenje analogije funkcije i njenog grafa je opasno i treba izvoditi oprezno. :-s Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije. :shock: Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid. 8) Primjere nadji sam. O:)[/quote]
dobro...tu se slazem. zato sam i koristio ovaj vrlo jednostavan primjer (f(x)=x+1, za koju je trivijalno pokazati da je neprekidna na cijeloj domeni).[/quote]
Tocno, ali ne mora imati neprekidni graf. :)
Jedino mjesto gdje bi definicija funkcije s praznom domenom mogla biti korisna je, IMO, to da ne moras mozgati kakav ti je skup S ako se zelis igrati s f|S (restrikcijom funkcije f na skup S). :)
| HijenA (napisa): | | vsego (napisa): | 1. Kodomena prazna, domena neprazna  nemoguce. nemoguce.  Neka je x iz domene (postoji, jer je ona neprazna); koja bi bila slika od x? Neka je x iz domene (postoji, jer je ona neprazna); koja bi bila slika od x?  |
to i mene interesira. eventualno bi moglo stajati da je slika od x nista, sto nema nikakvog smisla. niti bi matematicki bilo ikako upotrebljivo. |
Ne moze biti "nista".  Ako imas konkretan x, slika mu mora biti jednoznacno odredjena (pricamo o funkciji, ne?). Ako imas konkretan x, slika mu mora biti jednoznacno odredjena (pricamo o funkciji, ne?). 
| HijenA (napisa): | | vsego (napisa): | 2. Funkcija je relacija, a relacija je skup uredjenih parova, dakle i sama funkcija je (jako specifican) skup.  Iz te definicije (relacija koja za svaki x0 iz domene ima tocno jedan element (x, y) takav da je x = x0) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene. Iz te definicije (relacija koja za svaki x0 iz domene ima tocno jedan element (x, y) takav da je x = x0) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene.  |
ali, opet, moras pretpostaviti da su dva skupa jednaka. |
Huh? 
| HijenA (napisa): | | ne moze neki skup sa n elemenata biti u relaciji sa praznim skupom. |
Moze biti u praznoj relaciji, no onda to nije funkcija. 
| HijenA (napisa): | | isto tako, prazan skup ne moze biti u relaciji sa nekim skupom elemenata. |
Zasto ne? 
A = O // prazan skup
B = {1,2,...,n}
R subset AxB = O
Ovo mozemo smatrati funkcijom jer svakom elementu domene pridruzuje tocno jedan element kodomene.  Ako mi ne vjerujes, potrazi protuprimjer. Ako mi ne vjerujes, potrazi protuprimjer. 
Na praznim skupovima vrijede razna cuda...  Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17. Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17. 
| HijenA (napisa): | | vsego (napisa): | Inace, povlacenje analogije funkcije i njenog grafa je opasno i treba izvoditi oprezno.  Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije. Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije.  Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid. Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid.  Primjere nadji sam. Primjere nadji sam.  |
dobro...tu se slazem. zato sam i koristio ovaj vrlo jednostavan primjer (f(x)=x+1, za koju je trivijalno pokazati da je neprekidna na cijeloj domeni). |
Tocno, ali ne mora imati neprekidni graf. 
Jedino mjesto gdje bi definicija funkcije s praznom domenom mogla biti korisna je, IMO, to da ne moras mozgati kakav ti je skup S ako se zelis igrati s f|S (restrikcijom funkcije f na skup S). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 13:37 sub, 24. 12. 2005 Naslov: Postano: 13:37 sub, 24. 12. 2005 Naslov: |
    |
|
|
[quote="vsego"][quote="HijenA"][quote="vsego"]1. Kodomena prazna, domena neprazna :arrow: nemoguce. :? Neka je [i]x[/i] iz domene (postoji, jer je ona neprazna); koja bi bila slika od [i]x[/i]? :-k[/quote]
to i mene interesira. eventualno bi moglo stajati da je slika od x nista, sto nema nikakvog smisla. niti bi matematicki bilo ikako upotrebljivo.[/quote]
Ne moze biti "nista". :? Ako imas konkretan [i]x[/i], slika mu mora biti jednoznacno odredjena (pricamo o funkciji, ne?). :)[/quote]
slazem se :-)
[quote]
[quote="HijenA"][quote="vsego"]2. Funkcija je relacija, a relacija je skup uredjenih parova, dakle i sama funkcija je (jako specifican) skup. 8) Iz te definicije (relacija koja za svaki [i]x0[/i] iz domene ima tocno jedan element ([i]x[/i], [i]y[/i]) takav da je [i]x[/i] = [i]x0[/i]) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene. 8)[/quote]
ali, opet, moras pretpostaviti da su dva skupa jednaka.[/quote]
Huh? :grebgreb:[/quote]
nista...pomijesala mi se surjekcija i obicno preslikavanje :-) forget it :-)
[quote]
[quote="HijenA"]ne moze neki skup sa n elemenata biti u relaciji sa praznim skupom.[/quote]
Moze biti u praznoj relaciji, no onda to nije funkcija. 8)[/quote]
sta znaci prazna relacija?
[quote]
[quote="HijenA"]isto tako, prazan skup ne moze biti u relaciji sa nekim skupom elemenata.[/quote]
Zasto ne? :grebgreb:
A = O // prazan skup
B = {1,2,...,n}
R subset AxB = O
Ovo mozemo smatrati funkcijom jer svakom elementu domene pridruzuje tocno jedan element kodomene. :shock: Ako mi ne vjerujes, potrazi protuprimjer. :P[/quote]
daj, man, pa ti znas latex. ajde to prepisi jer ne kuzim sto si sa ovime htio reci :?
[quote]
Na praznim skupovima vrijede razna cuda... ;) Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17. :gg:[/quote]
zasto bas sa 17?
[quote]
Jedino mjesto gdje bi definicija funkcije s praznom domenom mogla biti korisna je, IMO, to da ne moras mozgati kakav ti je skup S ako se zelis igrati s f|S (restrikcijom funkcije f na skup S). :)[/quote]
no, opet moras (za tu restrikciju) provjeriti da li ima osnovna svojstva fcije, odnosno da li preslikava elemente sa skupa S na kodomenu tocno onako kako je fcijom definirano. ako to moras napraviti, onda moras odrediti domenu te restrikcije koja onda definitivno nije prazna (barem je ja tako ne mogu sebi predociti).
| vsego (napisa): | | HijenA (napisa): | | vsego (napisa): | 1. Kodomena prazna, domena neprazna  nemoguce. nemoguce.  Neka je x iz domene (postoji, jer je ona neprazna); koja bi bila slika od x? Neka je x iz domene (postoji, jer je ona neprazna); koja bi bila slika od x?  |
to i mene interesira. eventualno bi moglo stajati da je slika od x nista, sto nema nikakvog smisla. niti bi matematicki bilo ikako upotrebljivo. |
Ne moze biti "nista".  Ako imas konkretan x, slika mu mora biti jednoznacno odredjena (pricamo o funkciji, ne?). Ako imas konkretan x, slika mu mora biti jednoznacno odredjena (pricamo o funkciji, ne?).  |
slazem se 
| Citat: |
| HijenA (napisa): | | vsego (napisa): | 2. Funkcija je relacija, a relacija je skup uredjenih parova, dakle i sama funkcija je (jako specifican) skup.  Iz te definicije (relacija koja za svaki x0 iz domene ima tocno jedan element (x, y) takav da je x = x0) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene. Iz te definicije (relacija koja za svaki x0 iz domene ima tocno jedan element (x, y) takav da je x = x0) mozes lako izanalizirati sto bi bilo u slucaju prazne domene i/ili kodomene.  |
ali, opet, moras pretpostaviti da su dva skupa jednaka. |
Huh?  |
nista...pomijesala mi se surjekcija i obicno preslikavanje  forget it forget it 
| Citat: |
| HijenA (napisa): | | ne moze neki skup sa n elemenata biti u relaciji sa praznim skupom. |
Moze biti u praznoj relaciji, no onda to nije funkcija.  |
sta znaci prazna relacija?
| Citat: |
| HijenA (napisa): | | isto tako, prazan skup ne moze biti u relaciji sa nekim skupom elemenata. |
Zasto ne? 
A = O // prazan skup
B = {1,2,...,n}
R subset AxB = O
Ovo mozemo smatrati funkcijom jer svakom elementu domene pridruzuje tocno jedan element kodomene.  Ako mi ne vjerujes, potrazi protuprimjer. Ako mi ne vjerujes, potrazi protuprimjer.  |
daj, man, pa ti znas latex. ajde to prepisi jer ne kuzim sto si sa ovime htio reci 
| Citat: |
Na praznim skupovima vrijede razna cuda...  Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17. Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17.  |
zasto bas sa 17?
| Citat: |
Jedino mjesto gdje bi definicija funkcije s praznom domenom mogla biti korisna je, IMO, to da ne moras mozgati kakav ti je skup S ako se zelis igrati s f|S (restrikcijom funkcije f na skup S).  |
no, opet moras (za tu restrikciju) provjeriti da li ima osnovna svojstva fcije, odnosno da li preslikava elemente sa skupa S na kodomenu tocno onako kako je fcijom definirano. ako to moras napraviti, onda moras odrediti domenu te restrikcije koja onda definitivno nije prazna (barem je ja tako ne mogu sebi predociti).
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 13:51 sub, 24. 12. 2005 Naslov: Postano: 13:51 sub, 24. 12. 2005 Naslov: |
    |
|
|
[quote="HijenA"][quote="vsego"][quote="HijenA"]ne moze neki skup sa n elemenata biti u relaciji sa praznim skupom.[/quote]
Moze biti u praznoj relaciji, no onda to nije funkcija. 8)[/quote]
sta znaci prazna relacija?[/quote]
To, prema definiciji relacije, znaci prazan skup uredjenih parova. 8)
[quote="HijenA"][quote="vsego"][quote="HijenA"]isto tako, prazan skup ne moze biti u relaciji sa nekim skupom elemenata.[/quote]
Zasto ne? :grebgreb:
A = O // prazan skup
B = {1,2,...,n}
R subset AxB = O
Ovo mozemo smatrati funkcijom jer svakom elementu domene pridruzuje tocno jedan element kodomene. :shock: Ako mi ne vjerujes, potrazi protuprimjer. :P[/quote]
daj, man, pa ti znas latex. ajde to prepisi jer ne kuzim sto si sa ovime htio reci :?[/quote]
[latex]A = \emptyset \\
B = \{1,2,\dots,n\} \\
R \subset A\times B = \emptyset \Rightarrow R = \emptyset[/latex]
Dakle, opet prazna relacija, ovaj put s praznom domenom. :)
[quote="HijenA"][quote="vsego"]Na praznim skupovima vrijede razna cuda... ;) Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17. :gg:[/quote]
zasto bas sa 17?[/quote]
Svejedno. :roll: Samo primjer jednog nebuloznog "svojstva" praznog skupa. 8)
[quote="HijenA"][quote="vsego"]Jedino mjesto gdje bi definicija funkcije s praznom domenom mogla biti korisna je, IMO, to da ne moras mozgati kakav ti je skup S ako se zelis igrati s f|S (restrikcijom funkcije f na skup S). :)[/quote]
no, opet moras (za tu restrikciju) provjeriti da li ima osnovna svojstva fcije, odnosno da li preslikava elemente sa skupa S na kodomenu tocno onako kako je fcijom definirano. ako to moras napraviti, onda moras odrediti domenu te restrikcije koja onda definitivno nije prazna (barem je ja tako ne mogu sebi predociti).[/quote]
Ne. :? Upravo u tome i je poanta: na elementima praznog skupa vrijedi stogod zelis (ref. primjer s [b]prostim[/b] brojevima koji su [b]djeljivi[/b] s necim razlicitim od njih samih i jedinice). :D
| HijenA (napisa): | | vsego (napisa): | | HijenA (napisa): | | ne moze neki skup sa n elemenata biti u relaciji sa praznim skupom. |
Moze biti u praznoj relaciji, no onda to nije funkcija.  |
sta znaci prazna relacija? |
To, prema definiciji relacije, znaci prazan skup uredjenih parova. 
| HijenA (napisa): | | vsego (napisa): | | HijenA (napisa): | | isto tako, prazan skup ne moze biti u relaciji sa nekim skupom elemenata. |
Zasto ne? 
A = O // prazan skup
B = {1,2,...,n}
R subset AxB = O
Ovo mozemo smatrati funkcijom jer svakom elementu domene pridruzuje tocno jedan element kodomene.  Ako mi ne vjerujes, potrazi protuprimjer. Ako mi ne vjerujes, potrazi protuprimjer.  |
daj, man, pa ti znas latex. ajde to prepisi jer ne kuzim sto si sa ovime htio reci  |
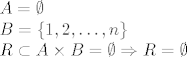
Dakle, opet prazna relacija, ovaj put s praznom domenom. 
| HijenA (napisa): | | vsego (napisa): | Na praznim skupovima vrijede razna cuda...  Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17. Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17.  |
zasto bas sa 17? |
Svejedno.  Samo primjer jednog nebuloznog "svojstva" praznog skupa. Samo primjer jednog nebuloznog "svojstva" praznog skupa. 
| HijenA (napisa): | | vsego (napisa): | Jedino mjesto gdje bi definicija funkcije s praznom domenom mogla biti korisna je, IMO, to da ne moras mozgati kakav ti je skup S ako se zelis igrati s f|S (restrikcijom funkcije f na skup S).  |
no, opet moras (za tu restrikciju) provjeriti da li ima osnovna svojstva fcije, odnosno da li preslikava elemente sa skupa S na kodomenu tocno onako kako je fcijom definirano. ako to moras napraviti, onda moras odrediti domenu te restrikcije koja onda definitivno nije prazna (barem je ja tako ne mogu sebi predociti). |
Ne.  Upravo u tome i je poanta: na elementima praznog skupa vrijedi stogod zelis (ref. primjer s prostim brojevima koji su djeljivi s necim razlicitim od njih samih i jedinice). Upravo u tome i je poanta: na elementima praznog skupa vrijedi stogod zelis (ref. primjer s prostim brojevima koji su djeljivi s necim razlicitim od njih samih i jedinice). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 12:09 uto, 27. 12. 2005 Naslov: Postano: 12:09 uto, 27. 12. 2005 Naslov: |
    |
|
|
[quote="vsego"]Inace, povlacenje analogije funkcije i njenog grafa je opasno i treba izvoditi oprezno. :-s Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije. :shock: Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid. 8) Primjere nadji sam. O:)[/quote]
Ne radi se o analogiji. Po pravoj matematickoj definiciji, funkcija [b]je[/b] graf. Graf realne funkcije jedne realne varijable je skup nekih parova realnih brojeva. Realacija je takodjer skup parova, i to tocno istih parova ako se radi o funkciji.
Ne znam za pojam neprekidnosti grafa. Vjerojatno si mislio na [b]povezanost[/b] grafa (kao podskupa od R^2 sa standardnom topologijom). Problem je neprecizan opis neprekidnih funkcija kao onih cije grafove mozemo nacrtati u jednom potezu. To bi odgovaralo povezanoscu putevima, a neprekidnost je zapravo ekvivalentna sa zatvorenosti grafa. S povezanosti nema puno veze, o cemu je vec bilo govora na [url=http://degiorgi.math.hr/forum/viewtopic.php?t=39]ovom[/url] topicu. Problem nije u opisu funkcije preko grafa. Taj je opis toliko precizan da su ga matematicari uzeli kao formalnu definiciju funkcije.
[quote="vsego"]Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17. :gg:[/quote]
Ovo je krivo na nekoliko razina. Broj 17 je prost i djeljiv je sa 17, a nije element praznog skupa. Ako zamijenis 17 sa 18 ili nekim drugim slozenim brojem, opet dobivas krivu tvrdnju. Prazan skup nije jedini koji sadrzi sve nepostojece brojeve, nego ih sadrze [b]svi[/b] skupovi (jer je prazan skup podskup svakog skupa).
@Hijena: stvari kao funkcija s praznom domenom potpuno su nezanimljive matematicki. To su trivijalni slucajevi koji se ponekad zabranjuju u definiciji upravo zato da se sprijeci diskusija poput ove tvoje :wink:
| vsego (napisa): | Inace, povlacenje analogije funkcije i njenog grafa je opasno i treba izvoditi oprezno.  Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije. Na primjer, neprekidnost grafa nije u direktnoj vezi s neprekidnoscu funkcije.  Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid. Npr. graf moze imati prekid, a da je funkcija neprekidna; takodjer, graf moze biti "u jednom komadu", a da funkcija ima prekid.  Primjere nadji sam. Primjere nadji sam.  |
Ne radi se o analogiji. Po pravoj matematickoj definiciji, funkcija je graf. Graf realne funkcije jedne realne varijable je skup nekih parova realnih brojeva. Realacija je takodjer skup parova, i to tocno istih parova ako se radi o funkciji.
Ne znam za pojam neprekidnosti grafa. Vjerojatno si mislio na povezanost grafa (kao podskupa od R^2 sa standardnom topologijom). Problem je neprecizan opis neprekidnih funkcija kao onih cije grafove mozemo nacrtati u jednom potezu. To bi odgovaralo povezanoscu putevima, a neprekidnost je zapravo ekvivalentna sa zatvorenosti grafa. S povezanosti nema puno veze, o cemu je vec bilo govora na ovom topicu. Problem nije u opisu funkcije preko grafa. Taj je opis toliko precizan da su ga matematicari uzeli kao formalnu definiciju funkcije.
| vsego (napisa): | Npr. prazni skup je jedini skup u kojem su svi prosti brojevi djeljivi sa 17.  |
Ovo je krivo na nekoliko razina. Broj 17 je prost i djeljiv je sa 17, a nije element praznog skupa. Ako zamijenis 17 sa 18 ili nekim drugim slozenim brojem, opet dobivas krivu tvrdnju. Prazan skup nije jedini koji sadrzi sve nepostojece brojeve, nego ih sadrze svi skupovi (jer je prazan skup podskup svakog skupa).
@Hijena: stvari kao funkcija s praznom domenom potpuno su nezanimljive matematicki. To su trivijalni slucajevi koji se ponekad zabranjuju u definiciji upravo zato da se sprijeci diskusija poput ove tvoje 
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
|













