| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 19:24 uto, 13. 12. 2005 Naslov: Re: Par pitanja Postano: 19:24 uto, 13. 12. 2005 Naslov: Re: Par pitanja |
    |
|
|
Pretpostavljam (jer postoje sitne varijante) da se matrica incidencije usmjerenog grafa sa skupom vrhova V i skupom bridova E definira kao matrica tipa |E|x|V| takva da je svakom bridu pridružen jedan redak, svakom vrhu pridružen jedan stupac i na presjeku nekog retka i nekog stupca piše:
1 ako brid "ulazi" u vrh
-1 ako brid "izlazi" iz vrha
0 inače (tj. nisu incidentni)
(Petlje se valjda ne dozvoljavaju kod usmjerenog grafa.)
Ako je pak graf neusmjeren, onda piše:
0 ako brid i vrh nisu incidentni
1 ako brid ima jedan kraj u tom vrhu
2 ako brid ima oba kraja i tom vrhu (tj. petlja je)
Ovo gore pišem samo da opravdam svoj odgovor u slučaju da je na predavanjima/vježbama bilo drukčije definirano.
[quote="Anonymous"]1)Kako iz matrice incidencije očitati povezanost grafa[/quote]
Graf je [b]nepovezan[/b] ako i samo ako se skup stupaca njegove matrice incidencije može rastaviti na dva skupa tako da ne postoje redak i dva stupca iz različitih skupova na čijem presjeku su -1 i 1.
[code:1] prvi | drugi
skup | skup
|
u | v
|
redak -1 | 1
|
|[/code:1]
Skupovi ne moraju biti kao na slici, tj. stupci mogu biti ispremiješani.
Dakle, graf je [b]povezan[/b] ako i samo ako se skup stupaca ne može...
A možemo i ovako:
Graf je [b]povezan[/b] ako i samo ako se u matrici incidencije putujući cik-cak (dakle, horizontalno-vertikalno) po 1-cama i -1-cama (za neusmjeren samo po 1-cama) može iz bilo kojeg stupca doći u bilo koji drugi.
Ilustracija tog "cik-cak":
[code:1]1->1
|
1--->1
|
1<-1 1->1
| |
1----->1[/code:1]
Mislim, to je sve skupa toliko logično (naprosto po definiciji) da je glupo što sam to uopće pisao. Ako ti nije jasno što sam gore slikovito htio reći, samo razmisli malo i sam ćeš doći do toga.
[quote="Anonymous"]2)Koji su nužni i dovoljni uvjeti da bi matrica bila mat. inc. a)grafa[/quote]
Za usmjereni graf: u svakom retku su joj jedna 1-ca i jedna -1-ca (ostalo su 0-e)
Za neusmjereni graf: u svakom retku su dvije 1-ce ili jedna 2-ka (ostalo su 0-e).
[quote="Anonymous"]b)povezanog grafa?[/quote]
Akko vrijedi ovo pod a) i ono iz prvog pitanja.
Pretpostavljam (jer postoje sitne varijante) da se matrica incidencije usmjerenog grafa sa skupom vrhova V i skupom bridova E definira kao matrica tipa |E|x|V| takva da je svakom bridu pridružen jedan redak, svakom vrhu pridružen jedan stupac i na presjeku nekog retka i nekog stupca piše:
1 ako brid "ulazi" u vrh
-1 ako brid "izlazi" iz vrha
0 inače (tj. nisu incidentni)
(Petlje se valjda ne dozvoljavaju kod usmjerenog grafa.)
Ako je pak graf neusmjeren, onda piše:
0 ako brid i vrh nisu incidentni
1 ako brid ima jedan kraj u tom vrhu
2 ako brid ima oba kraja i tom vrhu (tj. petlja je)
Ovo gore pišem samo da opravdam svoj odgovor u slučaju da je na predavanjima/vježbama bilo drukčije definirano.
| Anonymous (napisa): | | 1)Kako iz matrice incidencije očitati povezanost grafa |
Graf je nepovezan ako i samo ako se skup stupaca njegove matrice incidencije može rastaviti na dva skupa tako da ne postoje redak i dva stupca iz različitih skupova na čijem presjeku su -1 i 1.
| Kod: | prvi | drugi
skup | skup
|
u | v
|
redak -1 | 1
|
| |
Skupovi ne moraju biti kao na slici, tj. stupci mogu biti ispremiješani.
Dakle, graf je povezan ako i samo ako se skup stupaca ne može...
A možemo i ovako:
Graf je povezan ako i samo ako se u matrici incidencije putujući cik-cak (dakle, horizontalno-vertikalno) po 1-cama i -1-cama (za neusmjeren samo po 1-cama) može iz bilo kojeg stupca doći u bilo koji drugi.
Ilustracija tog "cik-cak":
| Kod: | 1->1
|
1--->1
|
1<-1 1->1
| |
1----->1 |
Mislim, to je sve skupa toliko logično (naprosto po definiciji) da je glupo što sam to uopće pisao. Ako ti nije jasno što sam gore slikovito htio reći, samo razmisli malo i sam ćeš doći do toga.
| Anonymous (napisa): | | 2)Koji su nužni i dovoljni uvjeti da bi matrica bila mat. inc. a)grafa |
Za usmjereni graf: u svakom retku su joj jedna 1-ca i jedna -1-ca (ostalo su 0-e)
Za neusmjereni graf: u svakom retku su dvije 1-ce ili jedna 2-ka (ostalo su 0-e).
| Anonymous (napisa): | | b)povezanog grafa? |
Akko vrijedi ovo pod a) i ono iz prvog pitanja.
Zadnja promjena: vjekovac; 19:41 uto, 13. 12. 2005; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:24 uto, 13. 12. 2005 Naslov: Re: Par pitanja Postano: 19:24 uto, 13. 12. 2005 Naslov: Re: Par pitanja |
    |
|
|
[quote="Anonymous"]2)Koji su nužni i dovoljni uvjeti da bi matrica bila mat. inc.
a)grafa [/quote]
Svaki brid ima točno dva vrha, tj. u svakom retku moraju biti dvije jedinice.
[quote]b)povezanog grafa?[/quote]
Mislim da zadatak pita za jednostavan graf.
Za jednostavan graf u svakom retku i svakom stupcu trebaju biti točno dvije jedinice.
[quote]1)Kako iz matrice incidencije očitati povezanost grafa i kako se iz nje određuje BFS i DFS?[/quote]
Graf je povezan ako u svakom retku imamo točno 2 jedinice, a u svakom stupcu proizvoljno mnogo jedinica.
Imaš recimo matricu
[code:1]
v1 v2 v3 v4 v5
e1 1 1 0 0 0
e2 0 1 1 0 0
e3 0 0 1 1 0
e4 1 0 0 1 0
e5 1 0 0 0 1
e6 0 0 0 1 1
[/code:1]
BFS kaže uzmi korijen, pronađi sve nove vrhove i skoči na jedan od njih.
Uzmeš za korijen npr v1.
On je incidentan sa e1,e4,e5.
Sad gledaš koji još vrhovi leže na e1,e4,e5. To su vrhovi v2,v4,v5.
Sad skočiš npr. na v2 i ponoviš postupak.
Imaj na umu da moraš dobiti stablo, tj. nesmije biti ciklusa, tako da ako skočiš na v2, možeš ići još samo do v3. dalje ni netrebaš jer su svi vrhovi odabrani.
DFS kaže uzmi korijen, nađi novi vrh i skoči na njega. Ako takvog nema, vrati se natrag.
Uzmeš opet v1.
v1 je preko e1 povezan s v2. skočiš na v2.
v2 je preko e2 povezan s v3. skočiš na v3.
v3 je preko e3 povezan s v4. skočiš na v4.
v4 više nije s nijednim novim vrhom povezan.
vraćaš se jedan korak nazad.
v3 nije s nijednim novim vrhom povezan.
korak nazad
v2 isto nije s nijednim novim vrhom povezan.
korak nazad
v1 je preko e5 povezan s v5. skočiš na v5.
gotovo.
(nisam 100% siguran u točnost ovoga svega).
prestigo me vjekovac + totalno sam zanemario usmjerenost i neusmjerenost :D
(mogu se izvuci na to da je zadatak zadan prije nego sto su se radili usmjereni grafovi :D )
| Anonymous (napisa): | 2)Koji su nužni i dovoljni uvjeti da bi matrica bila mat. inc.
a)grafa |
Svaki brid ima točno dva vrha, tj. u svakom retku moraju biti dvije jedinice.
| Citat: | | b)povezanog grafa? |
Mislim da zadatak pita za jednostavan graf.
Za jednostavan graf u svakom retku i svakom stupcu trebaju biti točno dvije jedinice.
| Citat: | | 1)Kako iz matrice incidencije očitati povezanost grafa i kako se iz nje određuje BFS i DFS? |
Graf je povezan ako u svakom retku imamo točno 2 jedinice, a u svakom stupcu proizvoljno mnogo jedinica.
Imaš recimo matricu
| Kod: |
v1 v2 v3 v4 v5
e1 1 1 0 0 0
e2 0 1 1 0 0
e3 0 0 1 1 0
e4 1 0 0 1 0
e5 1 0 0 0 1
e6 0 0 0 1 1
|
BFS kaže uzmi korijen, pronađi sve nove vrhove i skoči na jedan od njih.
Uzmeš za korijen npr v1.
On je incidentan sa e1,e4,e5.
Sad gledaš koji još vrhovi leže na e1,e4,e5. To su vrhovi v2,v4,v5.
Sad skočiš npr. na v2 i ponoviš postupak.
Imaj na umu da moraš dobiti stablo, tj. nesmije biti ciklusa, tako da ako skočiš na v2, možeš ići još samo do v3. dalje ni netrebaš jer su svi vrhovi odabrani.
DFS kaže uzmi korijen, nađi novi vrh i skoči na njega. Ako takvog nema, vrati se natrag.
Uzmeš opet v1.
v1 je preko e1 povezan s v2. skočiš na v2.
v2 je preko e2 povezan s v3. skočiš na v3.
v3 je preko e3 povezan s v4. skočiš na v4.
v4 više nije s nijednim novim vrhom povezan.
vraćaš se jedan korak nazad.
v3 nije s nijednim novim vrhom povezan.
korak nazad
v2 isto nije s nijednim novim vrhom povezan.
korak nazad
v1 je preko e5 povezan s v5. skočiš na v5.
gotovo.
(nisam 100% siguran u točnost ovoga svega).
prestigo me vjekovac + totalno sam zanemario usmjerenost i neusmjerenost 
(mogu se izvuci na to da je zadatak zadan prije nego sto su se radili usmjereni grafovi  ) )
_________________
The Dude Abides
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 22:15 uto, 13. 12. 2005 Naslov: Re: Par pitanja Postano: 22:15 uto, 13. 12. 2005 Naslov: Re: Par pitanja |
    |
|
|
Ovo sto pisem nisam 100% siguran, ali bar mislim da sam u pravu :P
[quote="Lord Sirius"]
[quote]b)povezanog grafa?[/quote]
Mislim da zadatak pita za jednostavan graf.
Za jednostavan graf u svakom retku i svakom stupcu trebaju biti točno dvije jedinice.[/quote]
Nisi u pravu, po ovome bi [latex]\left( \begin{array}{cc}1 & 1 \\ 1 & 1 \\ \end{array} \right)[/latex] bila matrica incidencije jednostavnog grafa, sto ocito nije.
Odgovor je - matrica incidencije koja nema dva jednaka retka.
[quote="Lord Sirius"]
[quote]1)Kako iz matrice incidencije očitati povezanost grafa i kako se iz nje određuje BFS i DFS?[/quote]
Graf je povezan ako u svakom retku imamo točno 2 jedinice, a u svakom stupcu proizvoljno mnogo jedinica.[/quote]
U svakom stupcu mozes imati proizvoljno mnogo jedinica, ali moras imati barem jednu.
[quote="Lord Sirius"]
BFS kaže uzmi korijen, pronađi sve nove vrhove i skoči na jedan od njih.
[/quote]
Tako smo rekli na vjezbama, ali ovaj opis BFSa mi se cini los. Da mi netko samo da ovaj opis, nikad ne bih shvatio kako BFS radi, ja bih rekao uzmi korijen, pronađi sve nove vrhove i skoči na [color=red]svaki[/color] od njih. Tj, za svaki od njih pronadi sve nove, pa za svaki od njih, itd. Ili to, ili sam ja totalno zabrijao i ne znam sto radi BFS :P
Ovo sto pisem nisam 100% siguran, ali bar mislim da sam u pravu 
| Lord Sirius (napisa): |
| Citat: | | b)povezanog grafa? |
Mislim da zadatak pita za jednostavan graf.
Za jednostavan graf u svakom retku i svakom stupcu trebaju biti točno dvije jedinice. |
Nisi u pravu, po ovome bi 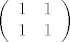 bila matrica incidencije jednostavnog grafa, sto ocito nije. bila matrica incidencije jednostavnog grafa, sto ocito nije.
Odgovor je - matrica incidencije koja nema dva jednaka retka.
| Lord Sirius (napisa): |
| Citat: | | 1)Kako iz matrice incidencije očitati povezanost grafa i kako se iz nje određuje BFS i DFS? |
Graf je povezan ako u svakom retku imamo točno 2 jedinice, a u svakom stupcu proizvoljno mnogo jedinica. |
U svakom stupcu mozes imati proizvoljno mnogo jedinica, ali moras imati barem jednu.
| Lord Sirius (napisa): |
BFS kaže uzmi korijen, pronađi sve nove vrhove i skoči na jedan od njih.
|
Tako smo rekli na vjezbama, ali ovaj opis BFSa mi se cini los. Da mi netko samo da ovaj opis, nikad ne bih shvatio kako BFS radi, ja bih rekao uzmi korijen, pronađi sve nove vrhove i skoči na svaki od njih. Tj, za svaki od njih pronadi sve nove, pa za svaki od njih, itd. Ili to, ili sam ja totalno zabrijao i ne znam sto radi BFS 
_________________
Bri
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 22:33 uto, 13. 12. 2005 Naslov: Re: Par pitanja Postano: 22:33 uto, 13. 12. 2005 Naslov: Re: Par pitanja |
    |
|
|
[quote="Grga"]
[quote="Lord Sirius"]
[quote]b)povezanog grafa?[/quote]
Mislim da zadatak pita za jednostavan graf.
Za jednostavan graf u svakom retku i svakom stupcu trebaju biti točno dvije jedinice.[/quote]
Nisi u pravu, po ovome bi [latex]\left( \begin{array}{cc}1 & 1 \\ 1 & 1 \\ \end{array} \right)[/latex] bila matrica incidencije jednostavnog grafa, sto ocito nije.
Odgovor je - matrica incidencije koja nema dva jednaka retka.[/quote]
Istina, imaš pravo.
[quote]
[quote="Lord Sirius"]
[quote]1)Kako iz matrice incidencije očitati povezanost grafa i kako se iz nje određuje BFS i DFS?[/quote]
Graf je povezan ako u svakom retku imamo točno 2 jedinice, a u svakom stupcu proizvoljno mnogo jedinica.[/quote]
U svakom stupcu mozes imati proizvoljno mnogo jedinica, ali moras imati barem jednu.[/quote]
Pod "mnogo" mislim na neki pozitivan termin ;) Nula nije mnogo ;)
[quote]
[quote="Lord Sirius"]
BFS kaže uzmi korijen, pronađi sve nove vrhove i skoči na jedan od njih.
[/quote]
Tako smo rekli na vjezbama, ali ovaj opis BFSa mi se cini los. Da mi netko samo da ovaj opis, nikad ne bih shvatio kako BFS radi, ja bih rekao uzmi korijen, pronađi sve nove vrhove i skoči na [color=red]svaki[/color] od njih. Tj, za svaki od njih pronadi sve nove, pa za svaki od njih, itd. Ili to, ili sam ja totalno zabrijao i ne znam sto radi BFS :P[/quote]
Da, na vježbama smo nadopisali "skoči na svaki od njih" iako niti to nije (meni) u potpunosti precizno. Npr. ništa ne znamo što prije trebamo raditi ako je v1 povezan sa v2 v3 v4 v5. Da li prije skočimo na v2 pa gledamo skim je on sve vezan pa se vraćamo nazad pa skočimo na v3 pa gledamo s kim je on sve vezan itd. ili da li ako skočimo na v2 gledamo s kim je on sve vezan (npr sa v7 v8 v500) pa odemo na v7 pa gledamo s kim je on vezan, pa ako nije s nikim, vratimo se na v2.
Uglavnom, nebitno. Nisam dovoljno precizan bio, najpreciznije je "skoči na sve nove vrhove."
| Grga (napisa): |
| Lord Sirius (napisa): |
| Citat: | | b)povezanog grafa? |
Mislim da zadatak pita za jednostavan graf.
Za jednostavan graf u svakom retku i svakom stupcu trebaju biti točno dvije jedinice. |
Nisi u pravu, po ovome bi 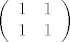 bila matrica incidencije jednostavnog grafa, sto ocito nije. bila matrica incidencije jednostavnog grafa, sto ocito nije.
Odgovor je - matrica incidencije koja nema dva jednaka retka. |
Istina, imaš pravo.
| Citat: |
| Lord Sirius (napisa): |
| Citat: | | 1)Kako iz matrice incidencije očitati povezanost grafa i kako se iz nje određuje BFS i DFS? |
Graf je povezan ako u svakom retku imamo točno 2 jedinice, a u svakom stupcu proizvoljno mnogo jedinica. |
U svakom stupcu mozes imati proizvoljno mnogo jedinica, ali moras imati barem jednu. |
Pod "mnogo" mislim na neki pozitivan termin  Nula nije mnogo Nula nije mnogo 
| Citat: |
| Lord Sirius (napisa): |
BFS kaže uzmi korijen, pronađi sve nove vrhove i skoči na jedan od njih.
|
Tako smo rekli na vjezbama, ali ovaj opis BFSa mi se cini los. Da mi netko samo da ovaj opis, nikad ne bih shvatio kako BFS radi, ja bih rekao uzmi korijen, pronađi sve nove vrhove i skoči na svaki od njih. Tj, za svaki od njih pronadi sve nove, pa za svaki od njih, itd. Ili to, ili sam ja totalno zabrijao i ne znam sto radi BFS  |
Da, na vježbama smo nadopisali "skoči na svaki od njih" iako niti to nije (meni) u potpunosti precizno. Npr. ništa ne znamo što prije trebamo raditi ako je v1 povezan sa v2 v3 v4 v5. Da li prije skočimo na v2 pa gledamo skim je on sve vezan pa se vraćamo nazad pa skočimo na v3 pa gledamo s kim je on sve vezan itd. ili da li ako skočimo na v2 gledamo s kim je on sve vezan (npr sa v7 v8 v500) pa odemo na v7 pa gledamo s kim je on vezan, pa ako nije s nikim, vratimo se na v2.
Uglavnom, nebitno. Nisam dovoljno precizan bio, najpreciznije je "skoči na sve nove vrhove."
_________________
The Dude Abides
|
|
| [Vrh] |
|
Gordan
Forumaš(ica)


Pridružen/a: 03. 11. 2002. (18:01:44)
Postovi: (192)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
|










