|
Evo rješenja tog limesa. To naravno [u]nije zadatak s rokova[/u] jer je pretežak za Analizu 1&2. Ali izgleda zgodno.
Koliko se sjećam, zadatak je iz zbirke [i]G.Polya, G.Szego "Problems and Theorems in Analysis"[/i], ima je u knjižnici (ako ništa drugo, prijevod na ruski se uvijek može posuditi).
Dokazat ćemo:
[latex]{\Large\displaystyle\lim_{n\to\infty}\frac{e^{n/4}\cdot\sqrt[n]{1^1\cdot 2^2\cdot\cdot\ldots\cdot n^n}}{n^{(n+1)/2}}=1}[/latex]
Sređivanjem (kako je napisao vsego) i logaritmiranjem (po bazi e), zadatak postaje:
[latex]{\Large\displaystyle\lim_{n\to\infty}\Big(\frac{n}{4}+\sum_{k=1}^{n}\frac{k}{n}\ln\frac{k}{n}\Big)=0}[/latex]
Definirajmo funkciju [latex]f(x)=x\ln x[/latex] za x>0 i dodefinirajmo f(0)=0. Odmah se vidi da je f neprekidna na [0,+oo> pa specijalno i na [0,1].
[latex]\int_{0}^{1}f(x)\,dx=\int_{0}^{1}x\ln x\,dx=\textrm{(parc int.)}=-\frac{1}{4}[/latex]
Dakle, trebamo pokazati:
[latex]\displaystyle\lim_{n\to\infty}n\cdot\left(\sum_{k=1}^{n}\frac{1}{n}f\Big(\frac{k}{n}\Big)-\int_{0}^{1}f(x)\,dx\right)=0[/latex]
[latex]\displaystyle\sum_{k=1}^{n}\frac{1}{n}f\Big(\frac{k}{n}\Big)-\int_{0}^{1}f(x)\,dx=\sum_{k=1}^{n}\int_{(k-1)/n}^{k/n}\Big(f\Big(\frac{k}{n}\Big)-f(x)\Big)\,dx[/latex]
Sada se ovo pod integralom ocijeni (primjenom Lagrangeovog teorema srednje vrijednosti) kao između
[latex](\ln\frac{k-1}{n}+1)(\frac{k}{n}-x)[/latex] i [latex](\ln\frac{k}{n}+1)(\frac{k}{n}-x)[/latex]
pa se izintegrira po x, pa prosumira po k=2,3,...,n i još pomnoži s n.
Dobiju se nejednakosti:
[latex]\displaystyle\frac{1}{2}\sum_{k=1}^{n-1}\frac{1}{n}\ln\frac{k}{n}+\frac{n-1}{2n}\leq n\cdot\sum_{k=2}^{n}\int_{(k-1)/n}^{k/n}\Big(f\Big(\frac{k}{n}\Big)-f(x)\Big)\,dx\leq\\ \leq\frac{1}{2}\sum_{k=2}^{n}\frac{1}{n}\ln\frac{k}{n}+\frac{n-1}{2n}[/latex]
Sada iskoristimo [latex]\lim_{n\to\infty}\sum_{k=1}^{n}\frac{1}{n}\ln\frac{k}{n}=\int_{0}^{1}\ln x\,dx=-1[/latex]
(Integralne sume konvergiraju prema integralu. Makar je ovaj integral nepravi, podintegralna funkcija je monotona, pa vrijedi isto.)
Prelaskom na [latex]\lim_{n\to\infty}[/latex] i primjenom Teorema o sendviču slijedi tvrdnja o limesu iz zadatka.
:changes:
Evo rješenja tog limesa. To naravno nije zadatak s rokova jer je pretežak za Analizu 1&2. Ali izgleda zgodno.
Koliko se sjećam, zadatak je iz zbirke G.Polya, G.Szego "Problems and Theorems in Analysis", ima je u knjižnici (ako ništa drugo, prijevod na ruski se uvijek može posuditi).
Dokazat ćemo:
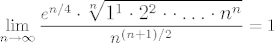
Sređivanjem (kako je napisao vsego) i logaritmiranjem (po bazi e), zadatak postaje:
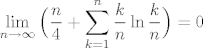
Definirajmo funkciju 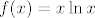 za x>0 i dodefinirajmo f(0)=0. Odmah se vidi da je f neprekidna na [0,+oo> pa specijalno i na [0,1]. za x>0 i dodefinirajmo f(0)=0. Odmah se vidi da je f neprekidna na [0,+oo> pa specijalno i na [0,1].
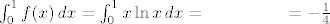
Dakle, trebamo pokazati:
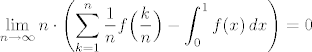
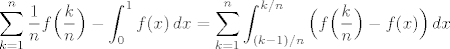
Sada se ovo pod integralom ocijeni (primjenom Lagrangeovog teorema srednje vrijednosti) kao između
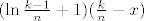 i i 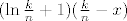
pa se izintegrira po x, pa prosumira po k=2,3,...,n i još pomnoži s n.
Dobiju se nejednakosti:
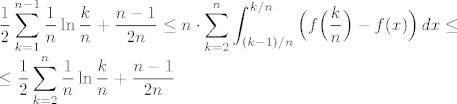
Sada iskoristimo 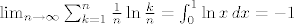
(Integralne sume konvergiraju prema integralu. Makar je ovaj integral nepravi, podintegralna funkcija je monotona, pa vrijedi isto.)
Prelaskom na 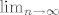 i primjenom Teorema o sendviču slijedi tvrdnja o limesu iz zadatka. i primjenom Teorema o sendviču slijedi tvrdnja o limesu iz zadatka.

|





