| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
grubač
Gost
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 2:18 ned, 8. 1. 2006 Naslov: Postano: 2:18 ned, 8. 1. 2006 Naslov: |
    |
|
|
Mi smo na predavanju tako definirali limes funkcije, al pretpostavljam da ste vi onda koristili epsilon delta definiciju.
Pretp. da vrijedi dano svojstvo za svaki takav niz.
Pretpostavimo suprotno, tj L nije limes, tj [latex](\exists \epsilon > 0)(\forall \delta > 0)(\exists x_\delta \in I)(( 0 < |x_\delta - c| < \delta )\land (|f(x_\delta) - L| > \epsilon))[/latex]
Gledamo niz [latex]\{x_n\} \subseteq I\setminus\{c\}[/latex] t.d. [latex]x_n = x_\delta[/latex] za [latex]\delta = \frac{1}{n}[/latex].
Limes tog niza je c, ali [latex]|f(x_n) - L| > \epsilon[/latex] tj, L nije limes niza [latex]f(x_n)[/latex] sto je kontradikcija.
Obratno, pretp. da je L limes funkcije u tocki c.
Uzmemo niz iz I\{c} koji tezi u c
[latex](\epsilon > 0) \Rightarrow (\exists \delta > 0)( x \in I, 0 <|x - c| < \delta \Rightarrow |f(x) - L| < \epsilon)[/latex]
A jer je limes niza c, [latex](\forall \delta > 0)(\exists n_0(\delta)[/latex] t.d. [latex]n \ge n_0 \Rightarrow |x_n - c| < \delta)[/latex].
Za dani epsilon uzmemo [latex]n_0(\delta)[/latex]. Tada imamo [latex]n \ge n_0 \Rightarrow |x_n - c|< \delta \Rightarrow |f(x_n) - L| < \epsilon[/latex]
Mi smo na predavanju tako definirali limes funkcije, al pretpostavljam da ste vi onda koristili epsilon delta definiciju.
Pretp. da vrijedi dano svojstvo za svaki takav niz.
Pretpostavimo suprotno, tj L nije limes, tj 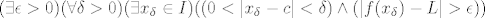
Gledamo niz 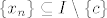 t.d. t.d. 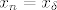 za za  . .
Limes tog niza je c, ali  tj, L nije limes niza tj, L nije limes niza 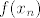 sto je kontradikcija. sto je kontradikcija.
Obratno, pretp. da je L limes funkcije u tocki c.
Uzmemo niz iz I\{c} koji tezi u c
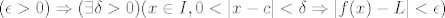
A jer je limes niza c, 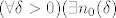 t.d. t.d. 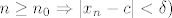 . .
Za dani epsilon uzmemo 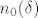 . Tada imamo . Tada imamo 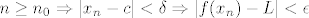
_________________
Bri
|
|
| [Vrh] |
|
grubač
Gost
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
grubač
Gost
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 19:51 pon, 9. 1. 2006 Naslov: Postano: 19:51 pon, 9. 1. 2006 Naslov: |
    |
|
|
[quote="grubač"]čuj Ignavia, naj se žifcirat 8) evo i tebi karma ++, al ću te zato doć gnjavit uskoro na demonstrature (već mi te žao) :D[/quote]
ma nema toga sto ne radim za karmu++, samo ti dodji :lol:
al pravilo je slijedece: kad pitas nesto, morat ces slusat odgovor [b]do kraja[/b], pri cemu je kraj kad ja kazem da je kraj, a ne kad ti kazes da si shvatio :verytwisted: :lol:
eh, svasta se moze od vjekovca naucit :PP :okgreen:
btw, do kraja semestra demonstrature Vanja i ja su srijedom 14-16... mislim da je to Vanja danas i stavila na oglasnu plocu
| grubač (napisa): | čuj Ignavia, naj se žifcirat  evo i tebi karma ++, al ću te zato doć gnjavit uskoro na demonstrature (već mi te žao) evo i tebi karma ++, al ću te zato doć gnjavit uskoro na demonstrature (već mi te žao)  |
ma nema toga sto ne radim za karmu++, samo ti dodji 
al pravilo je slijedece: kad pitas nesto, morat ces slusat odgovor do kraja, pri cemu je kraj kad ja kazem da je kraj, a ne kad ti kazes da si shvatio  
eh, svasta se moze od vjekovca naucit  
btw, do kraja semestra demonstrature Vanja i ja su srijedom 14-16... mislim da je to Vanja danas i stavila na oglasnu plocu
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 20:07 pon, 9. 1. 2006 Naslov: Postano: 20:07 pon, 9. 1. 2006 Naslov: |
    |
|
|
[quote="Ignavia"]btw, do kraja semestra demonstrature Vanja i ja su srijedom 14-16... mislim da je to Vanja danas i stavila na oglasnu plocu[/quote]
Evo, grubač, i ja ti preporučam da dođeš kod Ignavije i Vanje na demonstrature. :okgreen:
Ne samo tebi, nego svakome, općenito svakome... :D
(Nikad ne škodi malo reklame.)
Sponzor: :can: Medijski pokrovitelj: [size=24][color=darkblue][b]degiorgi[/b][/color][/size]
[size=7]Meni nemoj davat karmu++, kod mene je to ionako žali-bože...[/size]
| Ignavia (napisa): | | btw, do kraja semestra demonstrature Vanja i ja su srijedom 14-16... mislim da je to Vanja danas i stavila na oglasnu plocu |
Evo, grubač, i ja ti preporučam da dođeš kod Ignavije i Vanje na demonstrature. 
Ne samo tebi, nego svakome, općenito svakome... 
(Nikad ne škodi malo reklame.)
Sponzor:  Medijski pokrovitelj: degiorgi Medijski pokrovitelj: degiorgi
Meni nemoj davat karmu++, kod mene je to ionako žali-bože...
|
|
| [Vrh] |
|
|








