| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 15:09 sub, 7. 1. 2006 Naslov: Teorijska pitanja (vise njih) Postano: 15:09 sub, 7. 1. 2006 Naslov: Teorijska pitanja (vise njih) |
    |
|
|
imam jedno pitanje, sa pocetka gradiva.
dakle, prvi teorem u knjizi prof. Ungara:
Teorem 1.1: neka je [latex]A \subseteq \mathbb{R}[/latex] [color=blue]zatvoren[/color] neprazan skup koji je omedjen odozdo. Tada je [latex]\inf A \in A[/latex] , tj. skup A ima minimum. Analogno, ukoliko je A omedjen odozgo, onda je [latex]\sup A\in A[/latex] , tj. A ima maksimum.
Dokaz:
pretpostavimo da [latex]\inf A \notin A \Rightarrow \inf A \in \mathbb{R} \setminus A[/latex] . tada [latex]\exists r>0[/latex] takav da je [latex]\langle \inf A-r, \inf A+r \rangle \in \mathbb{R} \setminus A[/latex].
i sad me tu jedna stvar muci: skripta navodi da je broj [latex]\inf A+\frac{r}{2}[/latex] (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje.
meni sad nije jedna stvar jasna. sta ne bi trebali svi brojevi koji su veci od inf A automatski otpadati? a ne samo taj [latex]\frac{r}{2}[/latex]?
zahvaljujem.
PS. ocekujte jos pitanja od mene sto se tice gradiva MA3. budem sve postao ovdje, da nemamo 150 topica o istoj stvari :-)
[color=blue]HijenA[/color]: thanx, vsego :mrgreen:
imam jedno pitanje, sa pocetka gradiva.
dakle, prvi teorem u knjizi prof. Ungara:
Teorem 1.1: neka je  zatvoren neprazan skup koji je omedjen odozdo. Tada je zatvoren neprazan skup koji je omedjen odozdo. Tada je 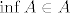 , tj. skup A ima minimum. Analogno, ukoliko je A omedjen odozgo, onda je , tj. skup A ima minimum. Analogno, ukoliko je A omedjen odozgo, onda je 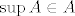 , tj. A ima maksimum. , tj. A ima maksimum.
Dokaz:
pretpostavimo da 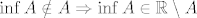 . tada . tada 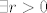 takav da je takav da je 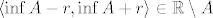 . .
i sad me tu jedna stvar muci: skripta navodi da je broj 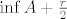 (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje. (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje.
meni sad nije jedna stvar jasna. sta ne bi trebali svi brojevi koji su veci od inf A automatski otpadati? a ne samo taj  ? ?
zahvaljujem.
PS. ocekujte jos pitanja od mene sto se tice gradiva MA3. budem sve postao ovdje, da nemamo 150 topica o istoj stvari 
HijenA: thanx, vsego 
Zadnja promjena: HijenA; 15:33 sub, 7. 1. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 15:24 sub, 7. 1. 2006 Naslov: Re: Teorijska pitanja (vise njih) Postano: 15:24 sub, 7. 1. 2006 Naslov: Re: Teorijska pitanja (vise njih) |
    |
|
|
[quote="HijenA"]Teorem 1.1: neka je [latex]A \subseteq \mathbb{R}[/latex] neprazan skup koji je omedjen odozdo. Tada je [latex]\inf A \in A[/latex] , tj. skup A ima minimum. Analogno, ukoliko je A omedjen odozgo, onda je [latex]\sup A\in A[/latex] , tj. A ima maksimum.[/quote]
Zanimljiva tvrdnja za koju cak i ja vidim da ne stoji. :-s Fali ti da je A zatvoren. 8)
[quote="HijenA"]i sad me tu jedna stvar muci: skripta navodi da je broj [latex]\inf A+\frac{r}{2}[/latex] (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje.
meni sad nije jedna stvar jasna. sta ne bi trebali svi brojevi koji su veci od inf A automatski otpadati? a ne samo taj [latex]\frac{r}{2}[/latex]?[/quote]
Pa, tebi je za pobiti pretpostavku dovoljan taj jedan broj; cemu se onda muciti s ostalima? :-k
| HijenA (napisa): | Teorem 1.1: neka je  neprazan skup koji je omedjen odozdo. Tada je neprazan skup koji je omedjen odozdo. Tada je 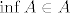 , tj. skup A ima minimum. Analogno, ukoliko je A omedjen odozgo, onda je , tj. skup A ima minimum. Analogno, ukoliko je A omedjen odozgo, onda je 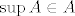 , tj. A ima maksimum. , tj. A ima maksimum. |
Zanimljiva tvrdnja za koju cak i ja vidim da ne stoji.  Fali ti da je A zatvoren. Fali ti da je A zatvoren. 
| HijenA (napisa): | i sad me tu jedna stvar muci: skripta navodi da je broj 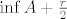 (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje. (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje.
meni sad nije jedna stvar jasna. sta ne bi trebali svi brojevi koji su veci od inf A automatski otpadati? a ne samo taj  ? ? |
Pa, tebi je za pobiti pretpostavku dovoljan taj jedan broj; cemu se onda muciti s ostalima? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 15:31 sub, 7. 1. 2006 Naslov: Re: Teorijska pitanja (vise njih) Postano: 15:31 sub, 7. 1. 2006 Naslov: Re: Teorijska pitanja (vise njih) |
    |
|
|
[quote="vsego"][quote="HijenA"]Teorem 1.1: neka je [latex]A \subseteq \mathbb{R}[/latex] neprazan skup koji je omedjen odozdo. Tada je [latex]\inf A \in A[/latex] , tj. skup A ima minimum. Analogno, ukoliko je A omedjen odozgo, onda je [latex]\sup A\in A[/latex] , tj. A ima maksimum.[/quote]
Zanimljiva tvrdnja za koju cak i ja vidim da ne stoji. :-s Fali ti da je A zatvoren. 8)[/quote]
uups...sorry :oops: da, treba pisat zatvoren :-) sad cu to ispravit i u gornjem postu :-)
[quote]
[quote="HijenA"]i sad me tu jedna stvar muci: skripta navodi da je broj [latex]\inf A+\frac{r}{2}[/latex] (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje.
meni sad nije jedna stvar jasna. sta ne bi trebali svi brojevi koji su veci od inf A automatski otpadati? a ne samo taj [latex]\frac{r}{2}[/latex]?[/quote]
Pa, tebi je za pobiti pretpostavku dovoljan taj jedan broj; cemu se onda muciti s ostalima? :-k[/quote]
ma, samo da vidim da li sam toliko zahrdjao sto se tice analize ili ne :-) dakle, za bilo koji r ovo gore vrijedi, jel tako? a r mozemo totalno proizvoljno uzeti, samo da je veci od 0. da li je to tocno?
| vsego (napisa): | | HijenA (napisa): | Teorem 1.1: neka je  neprazan skup koji je omedjen odozdo. Tada je neprazan skup koji je omedjen odozdo. Tada je 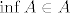 , tj. skup A ima minimum. Analogno, ukoliko je A omedjen odozgo, onda je , tj. skup A ima minimum. Analogno, ukoliko je A omedjen odozgo, onda je 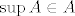 , tj. A ima maksimum. , tj. A ima maksimum. |
Zanimljiva tvrdnja za koju cak i ja vidim da ne stoji.  Fali ti da je A zatvoren. Fali ti da je A zatvoren.  |
uups...sorry  da, treba pisat zatvoren da, treba pisat zatvoren  sad cu to ispravit i u gornjem postu sad cu to ispravit i u gornjem postu 
| Citat: |
| HijenA (napisa): | i sad me tu jedna stvar muci: skripta navodi da je broj 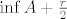 (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje. (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje.
meni sad nije jedna stvar jasna. sta ne bi trebali svi brojevi koji su veci od inf A automatski otpadati? a ne samo taj  ? ? |
Pa, tebi je za pobiti pretpostavku dovoljan taj jedan broj; cemu se onda muciti s ostalima?  |
ma, samo da vidim da li sam toliko zahrdjao sto se tice analize ili ne  dakle, za bilo koji r ovo gore vrijedi, jel tako? a r mozemo totalno proizvoljno uzeti, samo da je veci od 0. da li je to tocno? dakle, za bilo koji r ovo gore vrijedi, jel tako? a r mozemo totalno proizvoljno uzeti, samo da je veci od 0. da li je to tocno?
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 15:42 sub, 7. 1. 2006 Naslov: Re: Teorijska pitanja (vise njih) Postano: 15:42 sub, 7. 1. 2006 Naslov: Re: Teorijska pitanja (vise njih) |
    |
|
|
[quote="HijenA"][quote="vsego"][quote="HijenA"]i sad me tu jedna stvar muci: skripta navodi da je broj [latex]\inf A+\frac{r}{2}[/latex] (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje.
meni sad nije jedna stvar jasna. sta ne bi trebali svi brojevi koji su veci od inf A automatski otpadati? a ne samo taj [latex]\frac{r}{2}[/latex]?[/quote]
Pa, tebi je za pobiti pretpostavku dovoljan taj jedan broj; cemu se onda muciti s ostalima? :-k[/quote]
ma, samo da vidim da li sam toliko zahrdjao sto se tice analize ili ne :-) dakle, za bilo koji r ovo gore vrijedi, jel tako? a r mozemo totalno proizvoljno uzeti, samo da je veci od 0. da li je to tocno?[/quote]
Ne. :( Kad pocnes uciti MA3, vrijeme je da postanes pedantan, inace ti se lose pise. :trema:
Dakle, ovo gore vrijedi za [b]neki[/b] [i]r[/i]. :) Kad bi vrijedilo za svaki, ispalo bi da je [i]A[/i] prazan. :-s
Ti pretpostavljas da je A neprazan i zatvoren. :| Zbog zatvorenosti, njegov komplement (oznacimo ga sa [i]S[/i] := |R \ [i]A[/i]) je otvoren, pa oko svake tocke [i]x[/i] € [i]S[/i] [b]postoji[/b] otvorena okolina koja je podskup od [i]S[/i] (po definiciji otvorenog skupa). 8) Nitko ne kaze da je [b]svaka[/b] okolina od [i]x[/i] podskup od [i]S[/i], ne? ;)
Ako si pod "za bilo koji r ovo gore vrijedi" mislio "za bilo koji [i]x[/i] € <inf [i]A[/i], inf [i]A[/i] + r> vrijedi da je veci od inf [i]A[/i] i manji od svih elemenata iz [i]A[/i]", onda je to tocno, ali tu ipak treba biti precizan. :prodike:
| HijenA (napisa): | | vsego (napisa): | | HijenA (napisa): | i sad me tu jedna stvar muci: skripta navodi da je broj 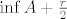 (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje. (koja je donja medja od A) bila veca od inf A koji je najveca donja medja, sto je u suprotnosti sa definicijom infimuma kao najvece donje medje.
meni sad nije jedna stvar jasna. sta ne bi trebali svi brojevi koji su veci od inf A automatski otpadati? a ne samo taj  ? ? |
Pa, tebi je za pobiti pretpostavku dovoljan taj jedan broj; cemu se onda muciti s ostalima?  |
ma, samo da vidim da li sam toliko zahrdjao sto se tice analize ili ne  dakle, za bilo koji r ovo gore vrijedi, jel tako? a r mozemo totalno proizvoljno uzeti, samo da je veci od 0. da li je to tocno? dakle, za bilo koji r ovo gore vrijedi, jel tako? a r mozemo totalno proizvoljno uzeti, samo da je veci od 0. da li je to tocno? |
Ne.  Kad pocnes uciti MA3, vrijeme je da postanes pedantan, inace ti se lose pise. Kad pocnes uciti MA3, vrijeme je da postanes pedantan, inace ti se lose pise. 
Dakle, ovo gore vrijedi za neki r.  Kad bi vrijedilo za svaki, ispalo bi da je A prazan. Kad bi vrijedilo za svaki, ispalo bi da je A prazan. 
Ti pretpostavljas da je A neprazan i zatvoren.  Zbog zatvorenosti, njegov komplement (oznacimo ga sa S := |R \ A) je otvoren, pa oko svake tocke x € S postoji otvorena okolina koja je podskup od S (po definiciji otvorenog skupa). Zbog zatvorenosti, njegov komplement (oznacimo ga sa S := |R \ A) je otvoren, pa oko svake tocke x € S postoji otvorena okolina koja je podskup od S (po definiciji otvorenog skupa).  Nitko ne kaze da je svaka okolina od x podskup od S, ne? Nitko ne kaze da je svaka okolina od x podskup od S, ne? 
Ako si pod "za bilo koji r ovo gore vrijedi" mislio "za bilo koji x € <inf A, inf A + r> vrijedi da je veci od inf A i manji od svih elemenata iz A", onda je to tocno, ali tu ipak treba biti precizan. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 16:11 sub, 7. 1. 2006 Naslov: Re: Teorijska pitanja (vise njih) Postano: 16:11 sub, 7. 1. 2006 Naslov: Re: Teorijska pitanja (vise njih) |
    |
|
|
[quote="vsego"]
Ako si pod "za bilo koji r ovo gore vrijedi" mislio "za bilo koji [i]x[/i] € <inf [i]A[/i], inf [i]A[/i] + r> vrijedi da je veci od inf [i]A[/i] i manji od svih elemenata iz [i]A[/i]", onda je to tocno, ali tu ipak treba biti precizan. :prodike:[/quote]
yup...na to. i znam da moram bit precizan, moram na to pripazit. jos jednom, hvala.
| vsego (napisa): |
Ako si pod "za bilo koji r ovo gore vrijedi" mislio "za bilo koji x € <inf A, inf A + r> vrijedi da je veci od inf A i manji od svih elemenata iz A", onda je to tocno, ali tu ipak treba biti precizan.  |
yup...na to. i znam da moram bit precizan, moram na to pripazit. jos jednom, hvala.
|
|
| [Vrh] |
|
kreso
Forumaš(ica)
Pridružen/a: 03. 10. 2004. (21:44:46)
Postovi: (7B)16
|
|
| [Vrh] |
|
mance
Gost
|
 Postano: 21:16 pon, 9. 1. 2006 Naslov: dva do Žitnjaka Postano: 21:16 pon, 9. 1. 2006 Naslov: dva do Žitnjaka |
    |
|
|
[quote="kreso"]imam i ja jedno pitanjce :?
zasto niz xk=1/k k E N u prostoru X=<0,2> podskup od Rn ne konvergira a istodobno je cauchyjev?
jel to samo zato sto mu 0 nije u prostoru X ili :?:
hvala[/quote]
Da i zbog jedinstvenosti limesa.
Kada bi on konvergirao u <0,2> prema nekom x_0 €<0,2>, tada on i konvergiro i u R, pa je zbog jedinstvenosti limesa, nužno x_0 =0, a kako 0 nije element od <0,2>, to dani niz ne konvergira u <0,2>.
| kreso (napisa): | imam i ja jedno pitanjce 
zasto niz xk=1/k k E N u prostoru X=<0,2> podskup od Rn ne konvergira a istodobno je cauchyjev?
jel to samo zato sto mu 0 nije u prostoru X ili 
hvala |
Da i zbog jedinstvenosti limesa.
Kada bi on konvergirao u <0,2> prema nekom x_0 €<0,2>, tada on i konvergiro i u R, pa je zbog jedinstvenosti limesa, nužno x_0 =0, a kako 0 nije element od <0,2>, to dani niz ne konvergira u <0,2>.
|
|
| [Vrh] |
|
kreso
Forumaš(ica)
Pridružen/a: 03. 10. 2004. (21:44:46)
Postovi: (7B)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 22:57 uto, 10. 1. 2006 Naslov: Postano: 22:57 uto, 10. 1. 2006 Naslov: |
    |
|
|
Evo ti slican primjer: jednadzba [latex]x^2 + 1 = 0[/latex] ima rjesenje, ali ne u [latex]\mathbb{R}[/latex] 8)
Slicno, ovaj niz ima limes u [latex]\mathbb{R}[/latex], ali ne i u [latex]\langle0, 2 \rangle[/latex]. :)
Jasnije? 8)
Evo ti slican primjer: jednadzba 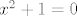 ima rjesenje, ali ne u ima rjesenje, ali ne u  
Slicno, ovaj niz ima limes u  , ali ne i u , ali ne i u 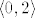 . . 
Jasnije? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
ne daj se Ilja
Gost
|
 Postano: 22:59 uto, 10. 1. 2006 Naslov: Postano: 22:59 uto, 10. 1. 2006 Naslov: |
    |
|
|
[quote="kreso"]a jel niz onda ima limes u 0 iako se nalazi u prostoru <0,2>, tj. taj limes idalje postoji?
zbujuje me to sto je receno da limes nemora biti e X, bar kod limesa funkcija... ili sam ja totalno pobrko stvari :?: :oops:[/quote]
po definiciji je niz u topološkom (metričkom) prostoru X konvergentan ako postoji x €X koji je limes tog niza, a definiciju limesa imaš.
Dakle, kako ne postoji x€<0,2>=X koji je limes tvog niza, on nije konvergentan u <0,2>.
| kreso (napisa): | a jel niz onda ima limes u 0 iako se nalazi u prostoru <0,2>, tj. taj limes idalje postoji?
zbujuje me to sto je receno da limes nemora biti e X, bar kod limesa funkcija... ili sam ja totalno pobrko stvari   |
po definiciji je niz u topološkom (metričkom) prostoru X konvergentan ako postoji x €X koji je limes tog niza, a definiciju limesa imaš.
Dakle, kako ne postoji x€<0,2>=X koji je limes tvog niza, on nije konvergentan u <0,2>.
|
|
| [Vrh] |
|
kreso
Forumaš(ica)
Pridružen/a: 03. 10. 2004. (21:44:46)
Postovi: (7B)16
|
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)

Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 19:45 uto, 28. 2. 2006 Naslov: Postano: 19:45 uto, 28. 2. 2006 Naslov: |
    |
|
|
Ok, mislim da bi ovako nešto najbolje tu spadalo:
Zašto je kompozicija dviju funkcija klase C^k funkcija klase C^k?
(122.str skripte, Taylorov tm. srednje vrijednosti)
Jel se to može nekako induktivno pokazati s obzirom da je kompozicija dviju dfb f-ja opet diferencijabilna, i dviju neprekidnih neprekidna? (to mi se čini ružno s obzirom da se počinje zapetljavat...)
Zapravo, ja tražim neko ljepše rješenje :gg:
zezam se, anything will do...
Unaprijed hvala!
Ok, mislim da bi ovako nešto najbolje tu spadalo:
Zašto je kompozicija dviju funkcija klase C^k funkcija klase C^k?
(122.str skripte, Taylorov tm. srednje vrijednosti)
Jel se to može nekako induktivno pokazati s obzirom da je kompozicija dviju dfb f-ja opet diferencijabilna, i dviju neprekidnih neprekidna? (to mi se čini ružno s obzirom da se počinje zapetljavat...)
Zapravo, ja tražim neko ljepše rješenje 
zezam se, anything will do...
Unaprijed hvala!
|
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)

Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)

Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
|
| [Vrh] |
|
C
Forumaš(ica)

Pridružen/a: 29. 01. 2005. (17:27:47)
Postovi: (4C)16
Spol: 
|
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)

Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
 Postano: 21:14 sri, 12. 4. 2006 Naslov: Postano: 21:14 sri, 12. 4. 2006 Naslov: |
    |
|
|
@C
Taj slučaj je, otprilike, manje više pokupljen u drugom dijelu dokaza, ali ne baš sasvim korektno. Naime, rekli smo
c:=inf(V).
"Stoga, kada bi bilo c element iz V onda bi postojao r>0 takav da je
<c-r,c+r> sadržan u V, pa bi infimum skupa V bio manji od c."
Prethodna tvrdnja je prepisana iz skripte i ona ne vrijedi općenito.
Problem je u tome da mogu uzeti
V={b}
pa je c=b, pa za svaki r>0 <c-r,c+r> siječe komplement od [a,b], tj. ne
mora postojati r>0 za kojeg vrijedi ta tvrdnja. Tvrdnja vrijedi ako znamo da c nije iz ruba od [a,b], tj. c!=b pa smo si zato prethodno dokazali c!=b. Iz sličnog razloga je prvo dokazano i c!=a.
primjer 1.4.
Pokazali smo da je otvoren skup u R^n povezan ako i samo ako je povezan putevima. Skup W iz primjera je zatvoren (zatvoren je jer mu je
komplement otvoren - ako uzmem neku točku iz komplementa onda postoji i nekakva kugla oko te točke koja je disjunktna sa W) pa je možda moguće da je povezan i nije povezan putevima.
Pretpostavimo da je W nepovezan i neka je
W=A u B
gdje su A,B disjunktni, otvoreni, neprazni. Neka je P=(1,sin(1)) sadržano u B. Tada postoji neprekidna surjekcija (Tm 2.14.)
f : W -> {0,1}.
Neka je bso f(1,sin(1))=1.
Neka postoji x>0 t.d. f(x,sin(x))=0. Uzmimo najveći takav x. Onda za svaki r>0 K((x,sin(x)),r) siječe B pa f nije neprekidna. Kontradikcija. Uzmimo da ne postoji najveći x t.d. je f(x,sin(x))=0. Onda sigurno postoji najmanji y takav da je f(y,sin(y))=1 (kada ne bi postojao segment bi bio nepovezan). Onda za svaki r>0 K((y,sin(y)),r) siječe A, tj. f nije neprekidna. Dakle f(x,sin(x))=1 za svaki x>0.
Neka je f(0,0)=0. Za svaki r>0 K((0,0),r) siječe B pa f nije neprekidna. Dakle f(0,0)=1.
Sada očito segment {(0,y) | -1<=y<=1} nije čitav sadržan niti u A niti u B (da je čitav sadržan u B onda bi A bio prazan). Neka je g restrikcija od f na segment {(0,y) | -1<=y<=1}. g je surjekcija, restrikcija neprekidne f-je je neprekidna f-ja (Nap 2.1.) pa je po Tm. 2.14. segment nepovezan jer je g neprekidna surjekcija. Kontradikcija. :!:
Mislim da je to to. Neka me netko ispravi ako sam negdje pogriješio. :?
@C
Taj slučaj je, otprilike, manje više pokupljen u drugom dijelu dokaza, ali ne baš sasvim korektno. Naime, rekli smo
c:=inf(V).
"Stoga, kada bi bilo c element iz V onda bi postojao r>0 takav da je
<c-r,c+r> sadržan u V, pa bi infimum skupa V bio manji od c."
Prethodna tvrdnja je prepisana iz skripte i ona ne vrijedi općenito.
Problem je u tome da mogu uzeti
V={b}
pa je c=b, pa za svaki r>0 <c-r,c+r> siječe komplement od [a,b], tj. ne
mora postojati r>0 za kojeg vrijedi ta tvrdnja. Tvrdnja vrijedi ako znamo da c nije iz ruba od [a,b], tj. c!=b pa smo si zato prethodno dokazali c!=b. Iz sličnog razloga je prvo dokazano i c!=a.
primjer 1.4.
Pokazali smo da je otvoren skup u R^n povezan ako i samo ako je povezan putevima. Skup W iz primjera je zatvoren (zatvoren je jer mu je
komplement otvoren - ako uzmem neku točku iz komplementa onda postoji i nekakva kugla oko te točke koja je disjunktna sa W) pa je možda moguće da je povezan i nije povezan putevima.
Pretpostavimo da je W nepovezan i neka je
W=A u B
gdje su A,B disjunktni, otvoreni, neprazni. Neka je P=(1,sin(1)) sadržano u B. Tada postoji neprekidna surjekcija (Tm 2.14.)
f : W → {0,1}.
Neka je bso f(1,sin(1))=1.
Neka postoji x>0 t.d. f(x,sin(x))=0. Uzmimo najveći takav x. Onda za svaki r>0 K((x,sin(x)),r) siječe B pa f nije neprekidna. Kontradikcija. Uzmimo da ne postoji najveći x t.d. je f(x,sin(x))=0. Onda sigurno postoji najmanji y takav da je f(y,sin(y))=1 (kada ne bi postojao segment bi bio nepovezan). Onda za svaki r>0 K((y,sin(y)),r) siječe A, tj. f nije neprekidna. Dakle f(x,sin(x))=1 za svaki x>0.
Neka je f(0,0)=0. Za svaki r>0 K((0,0),r) siječe B pa f nije neprekidna. Dakle f(0,0)=1.
Sada očito segment {(0,y) | -1⇐y⇐1} nije čitav sadržan niti u A niti u B (da je čitav sadržan u B onda bi A bio prazan). Neka je g restrikcija od f na segment {(0,y) | -1⇐y⇐1}. g je surjekcija, restrikcija neprekidne f-je je neprekidna f-ja (Nap 2.1.) pa je po Tm. 2.14. segment nepovezan jer je g neprekidna surjekcija. Kontradikcija. 
Mislim da je to to. Neka me netko ispravi ako sam negdje pogriješio. 
|
|
| [Vrh] |
|
C
Forumaš(ica)

Pridružen/a: 29. 01. 2005. (17:27:47)
Postovi: (4C)16
Spol: 
|
 Postano: 15:56 čet, 13. 4. 2006 Naslov: Postano: 15:56 čet, 13. 4. 2006 Naslov: |
    |
|
|
@Unnamed One:
Tvrdnja ne vrijedi opcenito, ali vrijedi ako bi V bio otvoren skup - sto i je pretpostavka :grebgreb:?
Tj. ako bi npr. imali samo drugi dio dokaza (od "Stoga...)
[quote]
Problem je u tome da mogu uzeti
V={b}
[/quote]
Ustvari ne mogu uzeti jer smo pretpostavili da je V otvoren skup, a {b} nije otvoren (opcenito u R) :grebgreb:?
Primjer 1.4 jos gruntam - jos nisam dosao do teorema 2.14 :oops:
Usp. kako pokazati da ako je W=UuV (U i V kao gore, otvoreni, disjunktni, neprazni) onda postoji e>0 t.d <0,e> <=U ili <0,e> <=V
Sretan Uskrs :)
@Unnamed One:
Tvrdnja ne vrijedi opcenito, ali vrijedi ako bi V bio otvoren skup - sto i je pretpostavka  ? ?
Tj. ako bi npr. imali samo drugi dio dokaza (od "Stoga...)
| Citat: |
Problem je u tome da mogu uzeti
V={b}
|
Ustvari ne mogu uzeti jer smo pretpostavili da je V otvoren skup, a {b} nije otvoren (opcenito u R)  ? ?
Primjer 1.4 jos gruntam - jos nisam dosao do teorema 2.14 
Usp. kako pokazati da ako je W=UuV (U i V kao gore, otvoreni, disjunktni, neprazni) onda postoji e>0 t.d <0,e> ⇐U ili <0,e> ⇐V
Sretan Uskrs 
|
|
| [Vrh] |
|
Unnamed One
Forumaš(ica)

Pridružen/a: 23. 06. 2005. (22:09:33)
Postovi: (3C)16
|
 Postano: 11:46 pet, 14. 4. 2006 Naslov: Postano: 11:46 pet, 14. 4. 2006 Naslov: |
    |
|
|
@C
Dakle, krenimo od "Stoga..."
"Stoga, kada bi bilo c element iz V onda bi postojao r>0 takav da je
<c-r,c+r> sadržan u V, pa bi infimum skupa V bio manji od c."
U prvom postu pitao si zašto je prije dokazano c!=b. Ja napisah da je to zato što kad bismo uzeli V={b},... Zatim ti kažeš da je obavezno V!={b} jer je V otvoren (što je OK), ali to je upravo onaj isti argument koji se nalazi u dokazu da je c!=b u skripti.
"Mora dakle biti c iz U. No tada bi postojao r>0 t.d. je <c-r,c+r> sadržan u U pa bi infimum skupa V bio veći od c."
Pitanje :?: : Zašto takav r postoji, tj. zašto ne bi c bio jednak a pa gornja tvrdnja ne stoji?
Pa zato što onda U ne bi bio otvoren jer da je U otvoren onda c ne bi mogao biti infimum od V, ali to je argument koji se nalazi dokazu c!=a.
Da nismo dokazali c!=a i c!=b onda bi prilikom dokazivanja da c nije iz V, tj. da c nije iz U trebali prokomentirati da je V otvoren pa je V!={b}, tj. da radi otvorenosti od U vrijedi da kada bi c bio iz U onda ne bi mogao biti infimum od V. Mi smo te iste argumente iskoristili gore, u dokazu c!=a i c!=b pa smo kasnije mogli bezbrižno uzeti <c-r,c+r> bez da se brinemo o rubovima segmenta. S druge strane, očito je da je c!=a, tj. c!=b pa to možda uopće nije trebalo dodatno objašnjavati, ali, kao što vidiš, u dokazu je maksimalno detaljno raspisan svaki korak pa se na prvi pogled neka pojašnjenja možda mogu činiti suvišnima.
Nisam skužio zadnja 2 retka :? (ne mislim na "Sretan Uskrs" :lol: - hvala i tebi, nego ono prije toga). Ako je W onaj skup W iz primjera 1.4 što onda točno znači <0,e><=U kad je U<=W<=R^2?
@C
Dakle, krenimo od "Stoga..."
"Stoga, kada bi bilo c element iz V onda bi postojao r>0 takav da je
<c-r,c+r> sadržan u V, pa bi infimum skupa V bio manji od c."
U prvom postu pitao si zašto je prije dokazano c!=b. Ja napisah da je to zato što kad bismo uzeli V={b},... Zatim ti kažeš da je obavezno V!={b} jer je V otvoren (što je OK), ali to je upravo onaj isti argument koji se nalazi u dokazu da je c!=b u skripti.
"Mora dakle biti c iz U. No tada bi postojao r>0 t.d. je <c-r,c+r> sadržan u U pa bi infimum skupa V bio veći od c."
Pitanje  : Zašto takav r postoji, tj. zašto ne bi c bio jednak a pa gornja tvrdnja ne stoji? : Zašto takav r postoji, tj. zašto ne bi c bio jednak a pa gornja tvrdnja ne stoji?
Pa zato što onda U ne bi bio otvoren jer da je U otvoren onda c ne bi mogao biti infimum od V, ali to je argument koji se nalazi dokazu c!=a.
Da nismo dokazali c!=a i c!=b onda bi prilikom dokazivanja da c nije iz V, tj. da c nije iz U trebali prokomentirati da je V otvoren pa je V!={b}, tj. da radi otvorenosti od U vrijedi da kada bi c bio iz U onda ne bi mogao biti infimum od V. Mi smo te iste argumente iskoristili gore, u dokazu c!=a i c!=b pa smo kasnije mogli bezbrižno uzeti <c-r,c+r> bez da se brinemo o rubovima segmenta. S druge strane, očito je da je c!=a, tj. c!=b pa to možda uopće nije trebalo dodatno objašnjavati, ali, kao što vidiš, u dokazu je maksimalno detaljno raspisan svaki korak pa se na prvi pogled neka pojašnjenja možda mogu činiti suvišnima.
Nisam skužio zadnja 2 retka  (ne mislim na "Sretan Uskrs" (ne mislim na "Sretan Uskrs"  - hvala i tebi, nego ono prije toga). Ako je W onaj skup W iz primjera 1.4 što onda točno znači <0,e><=U kad je U<=W<=R^2? - hvala i tebi, nego ono prije toga). Ako je W onaj skup W iz primjera 1.4 što onda točno znači <0,e><=U kad je U<=W<=R^2?
|
|
| [Vrh] |
|
|














