| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pefri
Forumaš(ica)
Pridružen/a: 09. 02. 2005. (22:34:29)
Postovi: (20)16
|
 Postano: 16:53 pet, 6. 1. 2006 Naslov: Kompaktni skupovi - zadaci |
    |
|
|
Pozdrav, imam dva zadatka koje rješavam i trebala bi mi pomoć:
[b]1. Neka je X metricki prostor i K_1,.., K_n kompaktni podskupovi od X.
Ispitaj da li je unija tih skupova kompaktan skup.[/b]
Ja sam isla preko teorema da je unija oznacena sa K kompaktna akko svaki niz (x_n) iz te unije ima barem jednu tocku gomilanja.
Promatram skup {x_n| neN} - ako je on beskonacan onda barem jedan od skupova K_1,...,K_n sadrži beskonacno mnogo clanova niza
(x_n). Neka je to K_i, (x_nk)e K_i.
K_i je kompaktan - (x_nk) ima bare jednu tocku gomilanja, a to je tocka gomilanja i od (x_n) pa slijedi da je K kompaktan.
Sto ako je {x_n| neN} konacan?
[b]2. Dokazala sam da u topoloskom prostoru presjek dvaju podskupova A i B nije kompaktan! Kako u zadacima pokazati da je
konacan ili beskonacan presjek kompaktnih skupova kompaktan ako je prostor Hausdorffov?[/b]
- Dodjem do koraka kada tvrdim da je X Hausdorffov i presjek tih skupova zatvoren, odakle bi htjela pokazati da je taj presjek
kompaktan!
U iscekivanju odgovora, pozdrav!
Pozdrav, imam dva zadatka koje rješavam i trebala bi mi pomoć:
1. Neka je X metricki prostor i K_1,.., K_n kompaktni podskupovi od X.
Ispitaj da li je unija tih skupova kompaktan skup.
Ja sam isla preko teorema da je unija oznacena sa K kompaktna akko svaki niz (x_n) iz te unije ima barem jednu tocku gomilanja.
Promatram skup {x_n| neN} - ako je on beskonacan onda barem jedan od skupova K_1,...,K_n sadrži beskonacno mnogo clanova niza
(x_n). Neka je to K_i, (x_nk)e K_i.
K_i je kompaktan - (x_nk) ima bare jednu tocku gomilanja, a to je tocka gomilanja i od (x_n) pa slijedi da je K kompaktan.
Sto ako je {x_n| neN} konacan?
2. Dokazala sam da u topoloskom prostoru presjek dvaju podskupova A i B nije kompaktan! Kako u zadacima pokazati da je
konacan ili beskonacan presjek kompaktnih skupova kompaktan ako je prostor Hausdorffov?
- Dodjem do koraka kada tvrdim da je X Hausdorffov i presjek tih skupova zatvoren, odakle bi htjela pokazati da je taj presjek
kompaktan!
U iscekivanju odgovora, pozdrav!
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)
Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
| Postano: 23:18 pet, 6. 1. 2006 Naslov: Re: Kompaktni skupovi - zadaci |
|
|
|
[quote="pefri"][b]1. Neka je X metricki prostor i K_1,.., K_n kompaktni podskupovi od X. Ispitaj da li je unija tih skupova kompaktan skup.[/b][/quote]
Odgovor je da.
Možemo radije koristiti karakterizaciju: podskup S metričkog prostora je kompaktan akko svaki niz u S ima konvergentni podniz s limesom u S.
(Draže mi je gledati podnizove umjesto gomilišta, ali to su ionako nijanse.)
Neka je (x_n) niz u uniji K1U...UKn. Barem jedan od skupova K1,...,Kn sadrži beskonačno mnogo članova niza. Neka je to recimo skup Ki. Tada članovi niza koji se nalaze u K_i čine neki podniz (y_k). Kako je Ki kompaktan skup, to postoji podniz (z_l) niza (y_k) koji konvergira prema nekoj točki a€Ki. No tada je (z_l) podniz od (x_n) koji konvergira prema limesu a€K1U...UKn.
Razlika od ovog tvojeg je što ja ne promatram različite vrijednosti koje poprimaju članovi niza. Tako da problem s konačno mnogo vrijednosti uopće ne postoji.
Inače, ovdje je prirodnije koristiti (Heine-Borelovu) definiciju kompaktnosti preko otvorenih pokrivača. Dokaz onda ide ovako:
Uzmemo bilo koji otvoreni pokrivač od K1U...UKn. Za svaki i=1,...,n je on pogotovo pokrivač od Ki pa se može reducirati na konačni potpokrivač. Kad se uniraju ti konačni potpokrivači za i=1,...,n dobije se konačni pokrivač od K1U...UKn.
[quote="pefri"][b]2. Dokazala sam da u topoloskom prostoru presjek dvaju podskupova A i B nije kompaktan!.[/b][/quote]
Valjda hoćeš reći ovo:
[b]U općenitom topološkom prostoru presjek dvaju kompaktnih podskupova A i B ne mora biti kompaktan (tj. postoji protupromjer).[/b]
[quote="pefri"][b]Kako u zadacima pokazati da je konacan ili beskonacan presjek kompaktnih skupova kompaktan ako je prostor Hausdorffov?[/b][/quote]
I sad valjda hoćeš dokazati:
[b]U Hausdorffovom topološkom prostoru presjek dvaju kompaktnih podskupova A i B je opet kompaktan.[/b]
Dokaz je posljedica dviju poznatih činjenica (ima ih u svakom udžbeniku iz topologije, ako će trebati mogu im i skicirati dokaz):
(1) U Hausdorffovom prostoru svaki kompaktan podskup je nužno zatvoren.
(2) Zatvoreni podskup kompaktnog prostora je opet kompaktan.
Sada dokaz ide ovako:
Neka su A i B kompaktni podskupovi Hausdorffovog prostora X. Specijalno su zatvoreni prema (1) pa je i njihov presjek AnB opet zatvoren. Ali sada je AnB zatvoren i u relativnoj topologiji topološkog potprostora A. Kako je A kompaktan, prema (2) je i AnB opet kompaktan.
Općenito (za beskonačan presjek) nije ništa teže dokazati. Bitno je samo da je jedan podskup kompaktan, a ostali da su zatvoreni.
| pefri (napisa): | | 1. Neka je X metricki prostor i K_1,.., K_n kompaktni podskupovi od X. Ispitaj da li je unija tih skupova kompaktan skup. |
Odgovor je da.
Možemo radije koristiti karakterizaciju: podskup S metričkog prostora je kompaktan akko svaki niz u S ima konvergentni podniz s limesom u S.
(Draže mi je gledati podnizove umjesto gomilišta, ali to su ionako nijanse.)
Neka je (x_n) niz u uniji K1U...UKn. Barem jedan od skupova K1,...,Kn sadrži beskonačno mnogo članova niza. Neka je to recimo skup Ki. Tada članovi niza koji se nalaze u K_i čine neki podniz (y_k). Kako je Ki kompaktan skup, to postoji podniz (z_l) niza (y_k) koji konvergira prema nekoj točki a€Ki. No tada je (z_l) podniz od (x_n) koji konvergira prema limesu a€K1U...UKn.
Razlika od ovog tvojeg je što ja ne promatram različite vrijednosti koje poprimaju članovi niza. Tako da problem s konačno mnogo vrijednosti uopće ne postoji.
Inače, ovdje je prirodnije koristiti (Heine-Borelovu) definiciju kompaktnosti preko otvorenih pokrivača. Dokaz onda ide ovako:
Uzmemo bilo koji otvoreni pokrivač od K1U...UKn. Za svaki i=1,...,n je on pogotovo pokrivač od Ki pa se može reducirati na konačni potpokrivač. Kad se uniraju ti konačni potpokrivači za i=1,...,n dobije se konačni pokrivač od K1U...UKn.
| pefri (napisa): | | 2. Dokazala sam da u topoloskom prostoru presjek dvaju podskupova A i B nije kompaktan!. |
Valjda hoćeš reći ovo:
U općenitom topološkom prostoru presjek dvaju kompaktnih podskupova A i B ne mora biti kompaktan (tj. postoji protupromjer).
| pefri (napisa): | | Kako u zadacima pokazati da je konacan ili beskonacan presjek kompaktnih skupova kompaktan ako je prostor Hausdorffov? |
I sad valjda hoćeš dokazati:
U Hausdorffovom topološkom prostoru presjek dvaju kompaktnih podskupova A i B je opet kompaktan.
Dokaz je posljedica dviju poznatih činjenica (ima ih u svakom udžbeniku iz topologije, ako će trebati mogu im i skicirati dokaz):
(1) U Hausdorffovom prostoru svaki kompaktan podskup je nužno zatvoren.
(2) Zatvoreni podskup kompaktnog prostora je opet kompaktan.
Sada dokaz ide ovako:
Neka su A i B kompaktni podskupovi Hausdorffovog prostora X. Specijalno su zatvoreni prema (1) pa je i njihov presjek AnB opet zatvoren. Ali sada je AnB zatvoren i u relativnoj topologiji topološkog potprostora A. Kako je A kompaktan, prema (2) je i AnB opet kompaktan.
Općenito (za beskonačan presjek) nije ništa teže dokazati. Bitno je samo da je jedan podskup kompaktan, a ostali da su zatvoreni.
|
|
| [Vrh] |
|
pefri
Forumaš(ica)
Pridružen/a: 09. 02. 2005. (22:34:29)
Postovi: (20)16
|
| Postano: 12:42 sub, 7. 1. 2006 Naslov: |
|
|
|
Hvala na uputama! Sad su mi kristalno jasni ovi zadaci!
Imam još jedno pitanje od kompaktnih skupova:
Znači, A presjek B ne mora biti kompaktan skup u topološkom prostoru X. Kako to pokazati primjerom? Ja sam imala pogrešan postupak
tj. pokazala sam da općenito to ne vrijedi:
A presjek B= (U Ai) presjek (UBj) {Ai},{Bj} otvoreni pokrivači od A,B
A presjek B= (presjek Ai^c) presjek (presjek Bj^c) - što je zatvoren skup ali mi to implicira da je skup kompaktan! Svaki zatvoren i omeđen skup je kompaktan.
[b]Zadatak iz knjige: Neka je (X,d) kompaktan metrički prostor i f:X-X funkcija sa svojstvom:
d(f(x),f(y))<d(x,y) za svaki x,y€X, x različito od y.
Dokažite da f ima jedinstvenu fiksnu točku u X.[/b]
Rj.
Pokažem da je f neprekidna. Zatim je potrebno pokazati egzistenciju fiksne točke te funkcije. f je neprekidna pa slijedi da je i funkcija
d(f(x),x) neprekidna. Kako je f neprekidna postoji minimum x0, pa zbog pretpostavke d(f(x0),x0) nije strogo veće od 0. Zašto??
Ja bi egzistenciju jednostavnije pokazala kontradikcijom... pretpostavimo da takva točka ne postoji tj. ne postoji točka za koju je d(f(x0),x0)=0
tj. d(x0,x0)=0 što je u kontradikciji s M2).
Gdje se u svemu tome koristi svojstvo kompaktnosti?
Jedinstvenost je jednostavno pokazati.
Hvala na uputama! Sad su mi kristalno jasni ovi zadaci!
Imam još jedno pitanje od kompaktnih skupova:
Znači, A presjek B ne mora biti kompaktan skup u topološkom prostoru X. Kako to pokazati primjerom? Ja sam imala pogrešan postupak
tj. pokazala sam da općenito to ne vrijedi:
A presjek B= (U Ai) presjek (UBj) {Ai},{Bj} otvoreni pokrivači od A,B
A presjek B= (presjek Ai^c) presjek (presjek Bj^c) - što je zatvoren skup ali mi to implicira da je skup kompaktan! Svaki zatvoren i omeđen skup je kompaktan.
Zadatak iz knjige: Neka je (X,d) kompaktan metrički prostor i f:X-X funkcija sa svojstvom:
d(f(x),f(y))<d(x,y) za svaki x,y€X, x različito od y.
Dokažite da f ima jedinstvenu fiksnu točku u X.
Rj.
Pokažem da je f neprekidna. Zatim je potrebno pokazati egzistenciju fiksne točke te funkcije. f je neprekidna pa slijedi da je i funkcija
d(f(x),x) neprekidna. Kako je f neprekidna postoji minimum x0, pa zbog pretpostavke d(f(x0),x0) nije strogo veće od 0. Zašto??
Ja bi egzistenciju jednostavnije pokazala kontradikcijom... pretpostavimo da takva točka ne postoji tj. ne postoji točka za koju je d(f(x0),x0)=0
tj. d(x0,x0)=0 što je u kontradikciji s M2).
Gdje se u svemu tome koristi svojstvo kompaktnosti?
Jedinstvenost je jednostavno pokazati.
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)
Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol:
|
| Postano: 14:15 sub, 7. 1. 2006 Naslov: |
|
|
|
[quote="pefri"]Znači, A presjek B ne mora biti kompaktan skup u topološkom prostoru X. Kako to pokazati primjerom?[/quote]
Hmmm. Treba konstruirati neki nastrani primjer topološkog prostora X. Meni recimo pada na pamet sljedeće:
Neka je X topološki prostor dobiven tako da uniramo dva segmenta (dvije dužine u R^2)
[0,1]x{0}={(t,0):t€[0,1]}
[0,1]x{1}={(t,1):t€[0,1]}
(koji nasljeđuju euklidsku topologiju iz R^2)
i potom identificiramo točke (t,0) i (t,1) za svaki t€[0,1>,
tj. kvocijentiramo po relaciji ekvivalencije koja identificira (t,0)~(t,1) za t€[0,1>.
Radi jednostavnosti pišemo t za klasu ekvivalencije {(t,0),(t,1)}.
Opisno rečeno, na taj način smo dobili nekakav "hibridni segment" [0,1] koji na desnoj strani umjesto 1 ima dva kraja (1,0) i (1,1).
[code:1]________________o
o[/code:1]
X nije Hausdorffov prostor kao što će slijediti iz protuprimjera.
Neka je A=[0,1> unija {(1,0)}, tj. slika od [0,1]x{0} po kvocijentnom preslikavanju (koje je neprekidno) pa je A kompaktan kao neprekidna slika kompakta.
Neka je B=[0,1> unija {(1,1)}, tj. slika od [0,1]x{1} po kvocijentnom preslikavanju (koje je neprekidno) pa je B kompaktan kao neprekidna slika kompakta.
Njihov presjek je [latex][0,1\rangle[/latex] (na kojem je topologija ista kao i euklidska), a taj skup nije kompaktan.
[quote="pefri"]Svaki zatvoren i omeđen skup je kompaktan.[/quote]
To vrijedi recimo u R^n, ali ne vrijedi u proizvoljnom metričkom prostoru.
---------------------------
[quote="pefri"]Zadatak iz knjige: Neka je (X,d) kompaktan metrički prostor i f:X-X funkcija sa svojstvom:
d(f(x),f(y))<d(x,y) za svaki x,y€X, x različito od y.
Dokažite da f ima jedinstvenu fiksnu točku u X.[/quote]
[quote="pefri"]Pokažem da je f neprekidna. Zatim je potrebno pokazati egzistenciju fiksne točke te funkcije.
f je neprekidna pa slijedi da je i funkcija [latex]X\to\mathbb{R}, \ x\mapsto d(f(x),x)[/latex] neprekidna. Kako je [b]ta funkcija[/b] neprekidna postoji njen minimum [b]koji se postiže u nekoj točki[/b] x0€X[/quote]
Ovdje koristimo kompaktnost. Na kompaktnom metričkom prostoru X neprekidna funkcija X->R postiže minimum i maksimum. To ne vrijedi za neprekidnu funkciju na bilo kakvom prostoru.
Nastavak dokaza je lagan. Neka je minimum funkcije [latex]X\to\mathbb{R}, \ x\mapsto d(f(x),x)[/latex] jednak m, tj. d(f(x0),x0)=m.
Ako je f(x0) različito od x0, onda je (uvjet zadatka za x=f(x0), y=x0):
m<=d(f(f(x0)),f(x0))<d(f(x0),x0)=m,
što je kontradikcija. Zato mora biti f(x0)=x0, tj. x0 je fiksna točka od f.
| pefri (napisa): | | Znači, A presjek B ne mora biti kompaktan skup u topološkom prostoru X. Kako to pokazati primjerom? |
Hmmm. Treba konstruirati neki nastrani primjer topološkog prostora X. Meni recimo pada na pamet sljedeće:
Neka je X topološki prostor dobiven tako da uniramo dva segmenta (dvije dužine u R^2)
[0,1]x{0}={(t,0):t€[0,1]}
[0,1]x{1}={(t,1):t€[0,1]}
(koji nasljeđuju euklidsku topologiju iz R^2)
i potom identificiramo točke (t,0) i (t,1) za svaki t€[0,1>,
tj. kvocijentiramo po relaciji ekvivalencije koja identificira (t,0)~(t,1) za t€[0,1>.
Radi jednostavnosti pišemo t za klasu ekvivalencije {(t,0),(t,1)}.
Opisno rečeno, na taj način smo dobili nekakav "hibridni segment" [0,1] koji na desnoj strani umjesto 1 ima dva kraja (1,0) i (1,1).
X nije Hausdorffov prostor kao što će slijediti iz protuprimjera.
Neka je A=[0,1> unija {(1,0)}, tj. slika od [0,1]x{0} po kvocijentnom preslikavanju (koje je neprekidno) pa je A kompaktan kao neprekidna slika kompakta.
Neka je B=[0,1> unija {(1,1)}, tj. slika od [0,1]x{1} po kvocijentnom preslikavanju (koje je neprekidno) pa je B kompaktan kao neprekidna slika kompakta.
Njihov presjek je 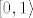 (na kojem je topologija ista kao i euklidska), a taj skup nije kompaktan.
| pefri (napisa): | | Svaki zatvoren i omeđen skup je kompaktan. |
To vrijedi recimo u R^n, ali ne vrijedi u proizvoljnom metričkom prostoru.
---------------------------
| pefri (napisa): | Zadatak iz knjige: Neka je (X,d) kompaktan metrički prostor i f:X-X funkcija sa svojstvom:
d(f(x),f(y))<d(x,y) za svaki x,y€X, x različito od y.
Dokažite da f ima jedinstvenu fiksnu točku u X. |
| pefri (napisa): | Pokažem da je f neprekidna. Zatim je potrebno pokazati egzistenciju fiksne točke te funkcije.
f je neprekidna pa slijedi da je i funkcija 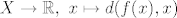 neprekidna. Kako je ta funkcija neprekidna postoji njen minimum koji se postiže u nekoj točki x0€X |
Ovdje koristimo kompaktnost. Na kompaktnom metričkom prostoru X neprekidna funkcija X→R postiže minimum i maksimum. To ne vrijedi za neprekidnu funkciju na bilo kakvom prostoru.
Nastavak dokaza je lagan. Neka je minimum funkcije 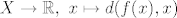jednak m, tj. d(f(x0),x0)=m.
Ako je f(x0) različito od x0, onda je (uvjet zadatka za x=f(x0), y=x0):
m⇐d(f(f(x0)),f(x0))<d(f(x0),x0)=m,
što je kontradikcija. Zato mora biti f(x0)=x0, tj. x0 je fiksna točka od f.
|
|
| [Vrh] |
|
pefri
Forumaš(ica)
Pridružen/a: 09. 02. 2005. (22:34:29)
Postovi: (20)16
|
| Postano: 20:49 ned, 8. 1. 2006 Naslov: |
|
|
|
[quote="vjekovac"]
Hmmm. Treba konstruirati neki nastrani primjer topološkog prostora X. Meni recimo pada na pamet sljedeće:
Neka je X topološki prostor dobiven tako da uniramo dva segmenta (dvije dužine u R^2)
[0,1]x{0}={(t,0):t€[0,1]}
[0,1]x{1}={(t,1):t€[0,1]}
(koji nasljeđuju euklidsku topologiju iz R^2)
i potom identificiramo točke (t,0) i (t,1) za svaki t€[0,1>,
tj. kvocijentiramo po relaciji ekvivalencije koja identificira (t,0)~(t,1) za t€[0,1>.
Radi jednostavnosti pišemo t za klasu ekvivalencije {(t,0),(t,1)}.
Opisno rečeno, na taj način smo dobili nekakav "hibridni segment" [0,1] koji na desnoj strani umjesto 1 ima dva kraja (1,0) i (1,1)....
[/quote]
Uhh... ovo mi se čini previše komplicirano! Sigurno postoji puno jednostavniji način jer unutar tog zadatka traži se da se isto pokaže za AUB, što se vrlo elegantno pokaže preko definicije kompaktnog skupa!
Hvala na pomoći u zadacima! :D
| vjekovac (napisa): |
Hmmm. Treba konstruirati neki nastrani primjer topološkog prostora X. Meni recimo pada na pamet sljedeće:
Neka je X topološki prostor dobiven tako da uniramo dva segmenta (dvije dužine u R^2)
[0,1]x{0}={(t,0):t€[0,1]}
[0,1]x{1}={(t,1):t€[0,1]}
(koji nasljeđuju euklidsku topologiju iz R^2)
i potom identificiramo točke (t,0) i (t,1) za svaki t€[0,1>,
tj. kvocijentiramo po relaciji ekvivalencije koja identificira (t,0)~(t,1) za t€[0,1>.
Radi jednostavnosti pišemo t za klasu ekvivalencije {(t,0),(t,1)}.
Opisno rečeno, na taj način smo dobili nekakav "hibridni segment" [0,1] koji na desnoj strani umjesto 1 ima dva kraja (1,0) i (1,1)....
|
Uhh... ovo mi se čini previše komplicirano! Sigurno postoji puno jednostavniji način jer unutar tog zadatka traži se da se isto pokaže za AUB, što se vrlo elegantno pokaže preko definicije kompaktnog skupa!
Hvala na pomoći u zadacima! 
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)
Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol:
|
|
| [Vrh] |
|
|
