| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Geliriell
Forumaš(ica)


Pridružen/a: 05. 10. 2005. (14:48:40)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:10 sri, 18. 1. 2006 Naslov: Re: Teorija Postano: 19:10 sri, 18. 1. 2006 Naslov: Re: Teorija |
    |
|
|
[quote="Geliriell"]Ovako mi pise propozicija u biljeznici: "Neka je a vektor iz V2(O) razlicit od nulvektora. Za svaki vektor b iz V2(O) postoji jedinstveni skalar λ iz R tako da b = λ * a."
Meni ovo nema smisla. Cini mi se da bi trebalo pisati da su a i b kolinearni ili tako nesto. Provjerila sam u tudje biljeznice pise isto ovako.[/quote]
Ako misliš da nema smisla, pretpostavi suprotno, tj. da postoji još jedan skalar [latex]\alpha \in \mathbb{R \backslash \{ \emptyset \} }, \alpha \neq \lambda[/latex] za koji vrijedi da je [latex]b=\alpha a[/latex].
Tada je:
[latex]
b=\lambda a \\
b=\alpha a \\
b - b=\lambda a - \alpha a \\
0 =a (\lambda - \alpha) \\ [/latex]
Sada ili je a=o ili [latex]\lambda - \alpha = 0[/latex]
Po pretpostavici a ne može biti nul vektor, pa je tada [latex]\lambda - \alpha = 0[/latex], tj. [latex]\lambda = \alpha[/latex]
Dovela si pretpostavku da postoji još jedan skalar do kontradikcije, dakle zaista postoji samo jedan skalar.
Što se tiče kolinearnosti, ona je definicija, a ovo što si napisala je propozicija.
Dakle, dva vektora a i b su kolinearna ako postoji skalar iz R\{0} tako da vrijedi da je [latex]b=\lambda a[/latex] - to je definicija.
To da je takav skalar jedinstven - to je propozicija! :)
| Geliriell (napisa): | Ovako mi pise propozicija u biljeznici: "Neka je a vektor iz V2(O) razlicit od nulvektora. Za svaki vektor b iz V2(O) postoji jedinstveni skalar λ iz R tako da b = λ * a."
Meni ovo nema smisla. Cini mi se da bi trebalo pisati da su a i b kolinearni ili tako nesto. Provjerila sam u tudje biljeznice pise isto ovako. |
Ako misliš da nema smisla, pretpostavi suprotno, tj. da postoji još jedan skalar 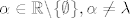 za koji vrijedi da je za koji vrijedi da je 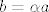 . .
Tada je:
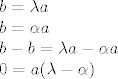
Sada ili je a=o ili 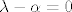
Po pretpostavici a ne može biti nul vektor, pa je tada 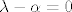 , tj. , tj. 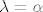
Dovela si pretpostavku da postoji još jedan skalar do kontradikcije, dakle zaista postoji samo jedan skalar.
Što se tiče kolinearnosti, ona je definicija, a ovo što si napisala je propozicija.
Dakle, dva vektora a i b su kolinearna ako postoji skalar iz R\{0} tako da vrijedi da je 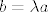 - to je definicija. - to je definicija.
To da je takav skalar jedinstven - to je propozicija! 
_________________
The Dude Abides
|
|
| [Vrh] |
|
Geliriell
Forumaš(ica)


Pridružen/a: 05. 10. 2005. (14:48:40)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:32 sri, 18. 1. 2006 Naslov: Postano: 19:32 sri, 18. 1. 2006 Naslov: |
    |
|
|
[quote="Geliriell"]Ali ako a i b nisu kolinearni, mi b mozemo mnoziti sa skalarom do mile volje, on (barem ja tako mislim) nikad nece postati a.[/quote]
Ahaaaa, krivo sam shvatio tvoje pitanje, ispričavam se. :)
Da, vjerojatno bi negdje trebalo pisati "Neka su a i b kolinearni vektori. Tada postoji jedinstveni skalar..." jer takav skalar ne postoji za sve vektore, npr. [1,0] i [0,1].
| Geliriell (napisa): | | Ali ako a i b nisu kolinearni, mi b mozemo mnoziti sa skalarom do mile volje, on (barem ja tako mislim) nikad nece postati a. |
Ahaaaa, krivo sam shvatio tvoje pitanje, ispričavam se. 
Da, vjerojatno bi negdje trebalo pisati "Neka su a i b kolinearni vektori. Tada postoji jedinstveni skalar..." jer takav skalar ne postoji za sve vektore, npr. [1,0] i [0,1].
_________________
The Dude Abides
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
|









