| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 20:07 čet, 19. 1. 2006 Naslov: Re: verižni razlomak Postano: 20:07 čet, 19. 1. 2006 Naslov: Re: verižni razlomak |
    |
|
|
[quote]imam dva pitanja:
razvoj u verižni razlomak broja sqrt(k^2+4), ako je k neparan prirodan broj.[/quote]
Koristi se algoritam (6.11) iz dokaza Teorema 6.14 iz skripte (slicno kao u Primjeru 6.6). Neka je k=2x+1. Dobiva se redom:
s_0=0, t_0=1, a_0=2x+1,
s_1=2x+1, t_1=4, a_1=x,
s_2=2x-1, t_2=2x+1, a_2=1,
s_3=2, t_3=2x+1, a_3=1,
s_4=2x-1, t_4=4, a_4=x,
s_5=2x+1, t_5=1, a_5=4x+2,
s_6=2x+1=s_1, t_6=4=t_1.
Zakljucujemo da je razvoj od sqrt((2x+1)^2+4) jednak
[2x+1;x,1,1,x,4x+2, ...] (ovaj segment x,1,1,x,4x+2 se ponavlja u nedogled).
Ovaj racun je tocan uz pretpostavku da je k>1, tj. x>0. Za x=0, tj. k^2+4=5, dobije se sqrt(5)=[2,4,4,4,4,...].
[quote]
je li razvoj u beskonačni verižni razlomak broja 2*(19^(1/11)) periodski?[/quote]
Koristi se Teorem 6.14 koji kaze da je razvoj od alpha periodski ako i samo ako je alpha rjesenje neke kvadratne jednadzbe s racionalnim koeficijentima.
| Citat: | imam dva pitanja:
razvoj u verižni razlomak broja sqrt(k^2+4), ako je k neparan prirodan broj. |
Koristi se algoritam (6.11) iz dokaza Teorema 6.14 iz skripte (slicno kao u Primjeru 6.6). Neka je k=2x+1. Dobiva se redom:
s_0=0, t_0=1, a_0=2x+1,
s_1=2x+1, t_1=4, a_1=x,
s_2=2x-1, t_2=2x+1, a_2=1,
s_3=2, t_3=2x+1, a_3=1,
s_4=2x-1, t_4=4, a_4=x,
s_5=2x+1, t_5=1, a_5=4x+2,
s_6=2x+1=s_1, t_6=4=t_1.
Zakljucujemo da je razvoj od sqrt((2x+1)^2+4) jednak
[2x+1;x,1,1,x,4x+2, ...] (ovaj segment x,1,1,x,4x+2 se ponavlja u nedogled).
Ovaj racun je tocan uz pretpostavku da je k>1, tj. x>0. Za x=0, tj. k^2+4=5, dobije se sqrt(5)=[2,4,4,4,4,...].
| Citat: |
je li razvoj u beskonačni verižni razlomak broja 2*(19^(1/11)) periodski? |
Koristi se Teorem 6.14 koji kaze da je razvoj od alpha periodski ako i samo ako je alpha rjesenje neke kvadratne jednadzbe s racionalnim koeficijentima.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
 Postano: 21:37 čet, 19. 1. 2006 Naslov: Postano: 21:37 čet, 19. 1. 2006 Naslov: |
    |
|
|
[quote]zašto je a0=2x+1? [/quote]
a_0 je najvece cijelo od sqrt((2x+1)^2+4).
Lako se vidi (nadam se :) ) da je
(2x+1)^2 < (2x+1)^2+4 < (2x+2)^2,
pa je zato a_0=2x+1.
[quote]kako se dobije a1.? kužim s i t, ali ako a računam kao
a= najveće_cijelo(s_i+naj_cijelo (sqrt(x))/t_i) ) tj. ako je
a_1=naj_cijelo((2x+1+2x+1)/4)
ajme sad sam se sva spetljala, uglavnom buni me kako smo odredili a_0 i kako uzimam najveće cijelo ako mi je x unutra,tako da ne znam odrediti a_1,a_2..[/quote]
Evo ovako:
a_1=najvece cijelo od ((2x+1+2x+1)/4) = najvece cijelo od (x+ 1/2) = x.
a_2=najvece cijelo od ((2x-1+2x+1)/(2x+1)) = najvece cijelo od (2- 2/(2x+1)) = 1.
a_3=najvece cijelo od ((2+2x+1)/(2x+1)) = najvece cijelo od (1+ 2/(2x+1)) = 1.
a_4=najvece cijelo od ((2x-1+2x+1)/4) = x.
a_5=najvece cijelo od ((2x+1+2x+1)/1) = 4x+2.
a_0 je najvece cijelo od sqrt((2x+1)^2+4).
Lako se vidi (nadam se  ) da je ) da je
(2x+1)^2 < (2x+1)^2+4 < (2x+2)^2,
pa je zato a_0=2x+1.
| Citat: | kako se dobije a1.? kužim s i t, ali ako a računam kao
a= najveće_cijelo(s_i+naj_cijelo (sqrt(x))/t_i) ) tj. ako je
a_1=naj_cijelo((2x+1+2x+1)/4)
ajme sad sam se sva spetljala, uglavnom buni me kako smo odredili a_0 i kako uzimam najveće cijelo ako mi je x unutra,tako da ne znam odrediti a_1,a_2.. |
Evo ovako:
a_1=najvece cijelo od ((2x+1+2x+1)/4) = najvece cijelo od (x+ 1/2) = x.
a_2=najvece cijelo od ((2x-1+2x+1)/(2x+1)) = najvece cijelo od (2- 2/(2x+1)) = 1.
a_3=najvece cijelo od ((2+2x+1)/(2x+1)) = najvece cijelo od (1+ 2/(2x+1)) = 1.
a_4=najvece cijelo od ((2x-1+2x+1)/4) = x.
a_5=najvece cijelo od ((2x+1+2x+1)/1) = 4x+2.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 19:08 ned, 28. 6. 2009 Naslov: Postano: 19:08 ned, 28. 6. 2009 Naslov: |
    |
|
|
zadatak glasi:
Razvijte u jednostavni verižni razlomak brojeve [latex]\sqrt{23}[/latex] i [latex]\frac{2+\sqrt{5}}{3}[/latex]
moje rješenje glasi:
[latex][4,\overline{1,3,1,8}] , $ $ [\overline{1,2,2,2,1,12}][/latex].
ako se ikome bude dalo dok vježba... zakon.
zadatak glasi:
Razvijte u jednostavni verižni razlomak brojeve 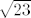 i i 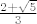
moje rješenje glasi:
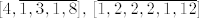 . .
ako se ikome bude dalo dok vježba... zakon.
_________________
ima let u finish
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 19:28 ned, 28. 6. 2009 Naslov: Postano: 19:28 ned, 28. 6. 2009 Naslov: |
    |
|
|
istina da sam odavno ovo polagao, ali mi je bilo malo sumnjivo ovo drugo rješenje, pa sam pokušao sam. što nije rezultat [latex]\[1; \overline{2, 2, 2, 1, 12, 1}\][/latex]?
EDIT....jao da, sad sam skužio :D
istina da sam odavno ovo polagao, ali mi je bilo malo sumnjivo ovo drugo rješenje, pa sam pokušao sam. što nije rezultat 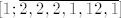 ? ?
EDIT....jao da, sad sam skužio 
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
duje
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (12:21:31)
Postovi: (55C)16
Spol: 
|
|
| [Vrh] |
|
ainotna
Forumaš(ica)


Pridružen/a: 25. 03. 2005. (19:38:22)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
ainotna
Forumaš(ica)


Pridružen/a: 25. 03. 2005. (19:38:22)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
uniqua
Forumaš(ica)
Pridružen/a: 18. 11. 2008. (11:26:10)
Postovi: (14)16
Spol: 
Lokacija: vinkovci
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 19:06 pon, 29. 6. 2009 Naslov: Postano: 19:06 pon, 29. 6. 2009 Naslov: |
    |
|
|
[quote="uniqua"]kad su ti s1 i t1 jednaki kao nekom sn i tn.[/quote]
ne, nego kad je (s_i,t_i) = (s_j,t_j) za neke i,j, i<j.
| uniqua (napisa): | | kad su ti s1 i t1 jednaki kao nekom sn i tn. |
ne, nego kad je (s_i,t_i) = (s_j,t_j) za neke i,j, i<j.
_________________
ima let u finish
|
|
| [Vrh] |
|
|













