|
[quote="Anonymous"]Moze li mi netko pomoci oko ovog zadatka s pismenog, 19.4.04 :
Ako je L:R^n -> R^n regularnan linearni operator, funkcije f,g € C^1(R^n) takve da je f(x)=Lx+ g(x), pri cemu postoji M>0 takav da vrijedi ||g(x)||<=M||x||^2, za svaki x€ R^n.
Dokazite da je f lokalni difeomorfizam oko nule.
Hvala![/quote]
Mada nisam u udruzi ateista, nadam se da ću vam pomoći. :shock: :drinking:
E da, dakle, dovoljno je pokazati da je diferencijal od g u točki 0, [latex]Dg(0)[/latex], trivijalan operator (nul-operator), jer je onda zbog aditivnosti diferenciranja i zbog linearnosti od L [latex]Df(0)=DL(0)+Dg(0)=DL(0)=L[/latex], a L je regularan po pretpostavci.
Kako bi dokazali da je [latex]Dg(0)=0[/latex], dovoljno je dokazati da je derivacija [latex]\partial_{e_i} g[/latex] od [latex]g[/latex] duž koordinatnog vektora [latex]e_i[/latex] jednaka [latex]0=(0,\ldots ,0) \in \mathbb{R}^n[/latex], za svako [latex]1 \leq i\leq n[/latex]. Kako je [latex]\|g(x)\| \leq M \|x\|^2, \ \forall x \in \mathbb{R}^n[/latex], to je svakako [latex]0\leq g(0)\leq 0[/latex], tj. [latex]g(0)=0[/latex]. Nadalje, zbog iste nejednakosti dobivamo i
[latex]0\leq \|\frac{g(te_i)-g(0)}{t}\| =\|\frac{g(te_i)}{t}\|\leq \frac{M \cdot t^2 \|e_i\|^2}{|t|}=M|t|, \ t \in \mathbb{R}\setminus \{ 0 \} [/latex]
Prelaskom na limes :drinking: (teorem o sendviču) dobivamo da je
[latex]\lim_{t \rightarrow 0}\|\frac{g(te_i)}{t}\|=0[/latex].
Zbog neprekidnosti norme i egzistencije derivacije [latex]\partial_{e_i}g(0)[/latex] je
[latex]0=\lim_{t \rightarrow 0}\|\frac{g(te_i)}{t}\|=\|\partial_{e_i}g(0)\|[/latex], tj. [latex]\partial_{e_i}g(0)=0[/latex], za sve [latex]1 \leq i\leq n[/latex]. Dakle, svaki svaki stupac matrice operatora
[latex]Dg(0)[/latex] (u kanonskoj bazi) je nulstupac, pa je [latex]Dg(0)[/latex] nul-operator. :drinking:
Srdačan pozdrav, vaš pravi prijatelj
dr. Exodus :croatia:
[size=7]меня эовут илья[/size]
| Anonymous (napisa): | Moze li mi netko pomoci oko ovog zadatka s pismenog, 19.4.04 :
Ako je L:R^n → R^n regularnan linearni operator, funkcije f,g € C^1(R^n) takve da je f(x)=Lx+ g(x), pri cemu postoji M>0 takav da vrijedi ||g(x)||⇐M||x||^2, za svaki x€ R^n.
Dokazite da je f lokalni difeomorfizam oko nule.
Hvala! |
Mada nisam u udruzi ateista, nadam se da ću vam pomoći.  
E da, dakle, dovoljno je pokazati da je diferencijal od g u točki 0, 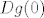 , trivijalan operator (nul-operator), jer je onda zbog aditivnosti diferenciranja i zbog linearnosti od L , trivijalan operator (nul-operator), jer je onda zbog aditivnosti diferenciranja i zbog linearnosti od L 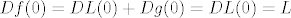 , a L je regularan po pretpostavci. , a L je regularan po pretpostavci.
Kako bi dokazali da je 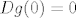 , dovoljno je dokazati da je derivacija , dovoljno je dokazati da je derivacija 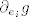 od od  duž koordinatnog vektora duž koordinatnog vektora 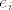 jednaka jednaka 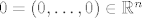 , za svako , za svako 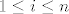 . Kako je . Kako je 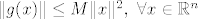 , to je svakako , to je svakako 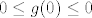 , tj. , tj. 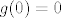 . Nadalje, zbog iste nejednakosti dobivamo i . Nadalje, zbog iste nejednakosti dobivamo i
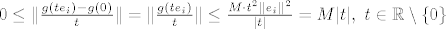
Prelaskom na limes  (teorem o sendviču) dobivamo da je (teorem o sendviču) dobivamo da je
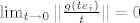 . .
Zbog neprekidnosti norme i egzistencije derivacije 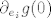 je je
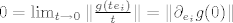 , tj. , tj. 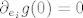 , za sve , za sve 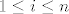 . Dakle, svaki svaki stupac matrice operatora . Dakle, svaki svaki stupac matrice operatora
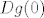 (u kanonskoj bazi) je nulstupac, pa je (u kanonskoj bazi) je nulstupac, pa je 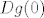 nul-operator. nul-operator. 
Srdačan pozdrav, vaš pravi prijatelj
dr. Exodus 
меня эовут илья
|




