|
[quote="Anonymous"]zadatak glasi: dokaži da je skup S kompaktan i nađi extreme fje f na tom skupu; S={(x,y,z): x+2y+3z=6,2xy+6yz+3zx=11} f(x,y,z)=xyz
ovo prvo s kompaktnošću opće nemam ideje kak bi dokazala,a da bi dobila extreme sam formirala lagrangeovu fju i onaj sustav sa pacijalnim derivacijama ali to onda ispada sustav 5 jedn. sa 5 nepoznanica što mi se nije činilo da bi riješila niti za par sati pa me zanima je li to pravi način rješavanja.
eto ako netko znade neka se ne srami pomoći :)[/quote]
Eh da, kao inače, vaš dr. Exodus :croatia: se ne srami pomoći kada je u pitanju analiza 3/4.
Budući se S nalazi konačnodimenzionalnom realnom normiranim prostoru ([latex]\mathbb{R}^3[/latex]), on će biti kompaktan akko je zatvoren i omeđen.
Zatvorenost je trivijalna, budući je [latex]S=\varphi^{-1}(\{0\})\cap \psi^{-1}(\{0\})[/latex], gdje su [latex]\varphi(x,y,z):=x+2y+3z-6, \ \psi(x,y,z):=2xy+6yz+3xz-11[/latex] neprekidne funkcije, pa budući su jednočlani skupovi zatvoreni u [latex]\mathbb{R}[/latex], to su i skupovi [latex]\varphi^{-1}(\{0\})[/latex] i [latex]\psi^{-1}(\{0\})[/latex] zatvoreni u [latex]\mathbb{R}^3[/latex], pa je i njihov presjek zatvoren u [latex]\mathbb{R}^3[/latex] (presjek zatvorenih skupova je zatvoren skup). :drinking:
Dokažimo omeđenost od [latex]S[/latex]. Neka je [latex]T:=(x,y,z)\in S[/latex] proizvoljna točka. Tada je
[latex]36=6^2=(x+2y+3z)^2=x^2+4y^2+9z^2+2(2xy+3xz+6yz)[/latex][latex]=x^2+4y^2+9z^2+22[/latex],
pa je [latex]x^2+4y^2+9z^2=14[/latex].
Drugim riječima, [latex]S[/latex] je podskup elipsoida [latex]\{(x,y,z) \in \mathbb{R}^3: \ x^2+4y^2+9z^2=14\}[/latex], koji je trivijalno omeđen jer je [latex]\|T\|^2=x^2+y^2+z^2 \leq x^2+4y^2+9z^2=14[/latex]. Time smo pokazali kompaktnost od [latex]S[/latex].
Sada definiramo Lagrangeovu funkciju
[latex]F(x,y,z,\lambda,\mu):=xyz-\lambda\varphi(x,y,z)-\mu\psi(x,y,z).[/latex] Parcijalne derivacije funkcije [latex]F[/latex] po svakoj varijabli izjednačimo s 0 i dobit ćemo sustav
[latex]yz-\lambda-\mu(2y+3z)=0[/latex]
[latex]xz-2\lambda-\mu(2x+6z)=0[/latex]
[latex]xy-3\lambda-\mu(6y+3x)=0[/latex]
[latex]x+2y+3z=6[/latex]
[latex]2xy+6yz+3xz=11[/latex].
E sad... prvu jednadžbu pomnožimo s -2 i dodamo drugoj, prvu pomnožimo s -3 i dodamo trećoj, te drugu pomnožimo s -3, treću s 2 i to zbrojimo... i dobit ćemo ekvivalentni sustav
[latex](x-2y)(z-2\mu)=0[/latex]
[latex](x-3z)(y-3\mu)=0[/latex]
[latex](2y-3z)(x-6\mu)=0[/latex]
[latex]x+2y+3z=6[/latex]
[latex]2xy+6yz+3xz=11[/latex]
I to sad valjda ne bi trebalo biti teško za rješiti. :D
Srdačan pozdrav, vaš drug i krug
dr. Exodus :croatia:
| Anonymous (napisa): | zadatak glasi: dokaži da je skup S kompaktan i nađi extreme fje f na tom skupu; S={(x,y,z): x+2y+3z=6,2xy+6yz+3zx=11} f(x,y,z)=xyz
ovo prvo s kompaktnošću opće nemam ideje kak bi dokazala,a da bi dobila extreme sam formirala lagrangeovu fju i onaj sustav sa pacijalnim derivacijama ali to onda ispada sustav 5 jedn. sa 5 nepoznanica što mi se nije činilo da bi riješila niti za par sati pa me zanima je li to pravi način rješavanja.
eto ako netko znade neka se ne srami pomoći  |
Eh da, kao inače, vaš dr. Exodus  se ne srami pomoći kada je u pitanju analiza 3/4. se ne srami pomoći kada je u pitanju analiza 3/4.
Budući se S nalazi konačnodimenzionalnom realnom normiranim prostoru (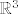 ), on će biti kompaktan akko je zatvoren i omeđen. ), on će biti kompaktan akko je zatvoren i omeđen.
Zatvorenost je trivijalna, budući je 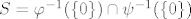 , gdje su , gdje su 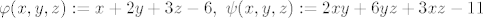 neprekidne funkcije, pa budući su jednočlani skupovi zatvoreni u neprekidne funkcije, pa budući su jednočlani skupovi zatvoreni u  , to su i skupovi , to su i skupovi 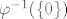 i i 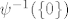 zatvoreni u zatvoreni u 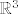 , pa je i njihov presjek zatvoren u , pa je i njihov presjek zatvoren u 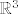 (presjek zatvorenih skupova je zatvoren skup). (presjek zatvorenih skupova je zatvoren skup). 
Dokažimo omeđenost od  . Neka je . Neka je 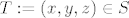 proizvoljna točka. Tada je proizvoljna točka. Tada je
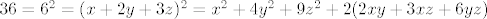 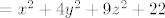 , ,
pa je  . .
Drugim riječima,  je podskup elipsoida je podskup elipsoida 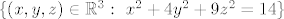 , koji je trivijalno omeđen jer je , koji je trivijalno omeđen jer je 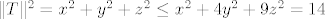 . Time smo pokazali kompaktnost od . Time smo pokazali kompaktnost od  . .
Sada definiramo Lagrangeovu funkciju
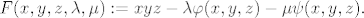 Parcijalne derivacije funkcije Parcijalne derivacije funkcije 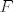 po svakoj varijabli izjednačimo s 0 i dobit ćemo sustav po svakoj varijabli izjednačimo s 0 i dobit ćemo sustav
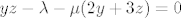
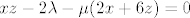
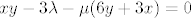
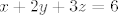
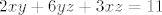 . .
E sad... prvu jednadžbu pomnožimo s -2 i dodamo drugoj, prvu pomnožimo s -3 i dodamo trećoj, te drugu pomnožimo s -3, treću s 2 i to zbrojimo... i dobit ćemo ekvivalentni sustav
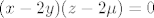
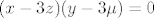
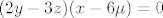
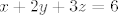
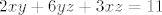
I to sad valjda ne bi trebalo biti teško za rješiti. 
Srdačan pozdrav, vaš drug i krug
dr. Exodus 
Zadnja promjena: Exodus; 23:17 pon, 30. 1. 2006; ukupno mijenjano 2 put/a.
|




