| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 23:44 sub, 4. 2. 2006 Naslov: Jedna teža determinanta Postano: 23:44 sub, 4. 2. 2006 Naslov: Jedna teža determinanta |
    |
|
|
Izračunaj determinantu
[latex]\left| \begin{array}{c c c c}
x & 1 & a & b \\
y^2 & y & 1 & c \\
yz^2 & z^2 & z & 1 \\
yzt & zt & t & 1 \\
\end{array} \right| [/latex]
Napomena: [latex] a, b, c [/latex] su konstante, a [latex] x, y, z, t [/latex] varijable.
Naravno, ne zanimaju me brut force rješenja tipa rastavljanje na matrice permutacija, 1000 upotreba Laplaceovog razvoja i slično...
Izračunaj determinantu
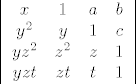
Napomena: 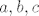 su konstante, a su konstante, a 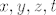 varijable. varijable.
Naravno, ne zanimaju me brut force rješenja tipa rastavljanje na matrice permutacija, 1000 upotreba Laplaceovog razvoja i slično...
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 3:06 ned, 5. 2. 2006 Naslov: Re: Jedna teža determinanta Postano: 3:06 ned, 5. 2. 2006 Naslov: Re: Jedna teža determinanta |
    |
|
|
[quote="Anonymous"]Izračunaj determinantu
[latex]\left| \begin{array}{c c c c}
x & 1 & a & b \\
y^2 & y & 1 & c \\
yz^2 & z^2 & z & 1 \\
yzt & zt & t & 1 \\
\end{array} \right| [/latex]
Napomena: [latex] a, b, c [/latex] su konstante, a [latex] x, y, z, t [/latex] varijable.
Naravno, ne zanimaju me brut force rješenja tipa rastavljanje na matrice permutacija, 1000 upotreba Laplaceovog razvoja i slično...[/quote]
Drugi stupac pomnozen sa -y dodas prvom, treci stupac pomnozen sa -z dodas drugom:
[latex]\left| \begin{array}{c c c c}
x-y & 1-za & a & b \\
0 & y-z & 1 & c \\
0 & 0 & z & 1 \\
0 & 0 & t & 1 \\
\end{array} \right| [/latex]
I sad je ocito rjesenje [latex](x-y)(y-z)(z-t)[/latex]
Valjda nisam fulao negdje... :P
| Anonymous (napisa): | Izračunaj determinantu
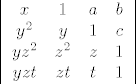
Napomena: 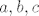 su konstante, a su konstante, a 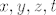 varijable. varijable.
Naravno, ne zanimaju me brut force rješenja tipa rastavljanje na matrice permutacija, 1000 upotreba Laplaceovog razvoja i slično... |
Drugi stupac pomnozen sa -y dodas prvom, treci stupac pomnozen sa -z dodas drugom:
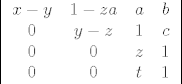
I sad je ocito rjesenje 
Valjda nisam fulao negdje... 
_________________
Bri
|
|
| [Vrh] |
|
|






