| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
 Postano: 15:30 čet, 26. 1. 2006 Naslov: tuga, jad... i ocaj... Postano: 15:30 čet, 26. 1. 2006 Naslov: tuga, jad... i ocaj... |
    |
|
|
bas me deprimira ovaj ODJ... prvo mi - dok šibam po vježbama i rješavam domaće radove - ide ko po loju... jer je vrlo jasno kojim metodama treba rješavat zadatak... i onda sva zadovoljna pređem na stare kolokvije...
...i onda pojedem pola kila napolitanki jer cijeli dan nisam uspila ni jedan zadatak rijesit do kraja... ili sam iskusala 18 metoda pa ni jedna nije upalila... ili u pocetku ide sve okej dok ne dodem do mjesta gdje gubim inspiraciju... znam da se svi ti problemi rjesavaju iskustvom, da je ponekad dovoljno samo malo odmorit glavu od problema nad kojim se tutnji vec sat vremena i onda rjesenje dode samo od sebe... zato sad necu nikoga zamarat problemima koji nisu jos prosli kroz tu proceduru... al evo par zadataka koji jesu, pa nije pomoglo....
2. zadatak iz proslogodisnjeg 2. kolokvija (jedna od 4 grupe):
[latex](e^{2y} + e^y -2xe^y + x^2)y'=1[/latex]
moj um je zakljucio da tu treba uvesti supstituciju [latex]u=e^y[/latex] (tj. stvarno ne znam sta bi drugo mogla)
time dodemo do jednadzbe [latex](u^2+u-2xu+x^2)u'=u[/latex]
pokusala sam nac eulerov multiplikator ali sam dobila gnjusan integral, pa sam zakljucila da sigurno postoji bolja metoda. homogeno nije, poopćeno homogeno nije, totalni diferencijal ne vidim...
2. zadatak iz proslogodisnjeg 2. kolokvija (neka druga od 4 grupe):
[latex](2x^2ylny-x)y'=y[/latex]
opet... potpuni diferencijal nisam otkrila, na egzaktnu nisam uspila svest, pokusah sa supstitucijom [latex]u=lny[/latex] međutim to me nije odvelo daleko...
pa eto hvala na svakoj pomoći... nemojte zamjerit ako sam previdjela nesto jako ocito :)
bas me deprimira ovaj ODJ... prvo mi - dok šibam po vježbama i rješavam domaće radove - ide ko po loju... jer je vrlo jasno kojim metodama treba rješavat zadatak... i onda sva zadovoljna pređem na stare kolokvije...
...i onda pojedem pola kila napolitanki jer cijeli dan nisam uspila ni jedan zadatak rijesit do kraja... ili sam iskusala 18 metoda pa ni jedna nije upalila... ili u pocetku ide sve okej dok ne dodem do mjesta gdje gubim inspiraciju... znam da se svi ti problemi rjesavaju iskustvom, da je ponekad dovoljno samo malo odmorit glavu od problema nad kojim se tutnji vec sat vremena i onda rjesenje dode samo od sebe... zato sad necu nikoga zamarat problemima koji nisu jos prosli kroz tu proceduru... al evo par zadataka koji jesu, pa nije pomoglo....
2. zadatak iz proslogodisnjeg 2. kolokvija (jedna od 4 grupe):
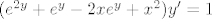
moj um je zakljucio da tu treba uvesti supstituciju 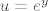 (tj. stvarno ne znam sta bi drugo mogla) (tj. stvarno ne znam sta bi drugo mogla)
time dodemo do jednadzbe 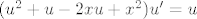
pokusala sam nac eulerov multiplikator ali sam dobila gnjusan integral, pa sam zakljucila da sigurno postoji bolja metoda. homogeno nije, poopćeno homogeno nije, totalni diferencijal ne vidim...
2. zadatak iz proslogodisnjeg 2. kolokvija (neka druga od 4 grupe):

opet... potpuni diferencijal nisam otkrila, na egzaktnu nisam uspila svest, pokusah sa supstitucijom 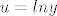 međutim to me nije odvelo daleko... međutim to me nije odvelo daleko...
pa eto hvala na svakoj pomoći... nemojte zamjerit ako sam previdjela nesto jako ocito 
_________________  "Download the files to a non-networked, firewalled computer."
- Dr. Elizabeth Weir |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 18:43 čet, 26. 1. 2006 Naslov: Re: tuga, jad... i ocaj... Postano: 18:43 čet, 26. 1. 2006 Naslov: Re: tuga, jad... i ocaj... |
    |
|
|
[quote="koryanshea"]2. zadatak iz proslogodisnjeg 2. kolokvija (neka druga od 4 grupe): [latex](2x^2ylny-x)y'=y[/latex][/quote]
[latex]
y' = \frac{y}{2x^2y\ln{y}-x}=- \frac{y}{x-2x^2y\ln{y}} \\
\frac{d}{dy}f_1(x,y)=1 \\
\frac{d}{dx}f_2(x,y)=1-4xy\ln{y} \\
[/latex]
Jednadžba nije egzaktna.
[latex]
\frac{d}{dy}f_1(x,y) - \frac{d}{dx}f_2(x,y) = 4xy\ln{y} \\
v=xy \\
\frac{dv}{dx} = y \\
\frac{dv}{dy} = x \\
\varphi(xy) = \frac{A}{yf_2 - xf_1} \\
\frac{1}{\mu}\mu' = \frac{4xylny}{y(x-2x^2y\ln{y}-xy} = \frac{-2}{xy} = \frac{-2}{v} \\
\int{\frac{1}{\mu}d\mu}=-2\int{\frac{1}{v}dv}
[/latex]
Dalje mislim da ide jednostavno, tj. svede se na egzaktnu i rješi se :)
Nisam provjeravao jer me večera čeka, a bome i MA3 :)
| koryanshea (napisa): | 2. zadatak iz proslogodisnjeg 2. kolokvija (neka druga od 4 grupe):  |
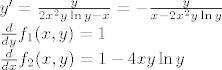
Jednadžba nije egzaktna.
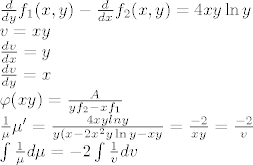
Dalje mislim da ide jednostavno, tj. svede se na egzaktnu i rješi se 
Nisam provjeravao jer me večera čeka, a bome i MA3 
_________________
The Dude Abides
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 16:41 sri, 1. 2. 2006 Naslov: Re: tuga, jad... i ocaj... Postano: 16:41 sri, 1. 2. 2006 Naslov: Re: tuga, jad... i ocaj... |
    |
|
|
[quote="koryanshea"]
2. zadatak iz proslogodisnjeg 2. kolokvija (jedna od 4 grupe):
[latex](e^{2y} + e^y -2xe^y + x^2)y'=1[/latex][/quote]
Nakon uvođenja substitucije
[latex]u=e^y[/latex] i jednadžbe [latex](u^2+u-2xu+x^2)u'=u[/latex] imaš dalje ovo:
[latex](u^2+u-2xu+x^2)du=udx \\
(u^2+u-2xu+x^2)du - udx = 0\\
\frac{df1}{du}=-1 \\
\frac{df2}{dx}=-2u+2x \\
A=-1+2u-2x=-1+2(u-x)
[/latex]
Sad nakon što sam razbijao glavu sa šablonama i supstitucijama koje su se radile na vježbama, odlučio sam odustati od zadatka i otići na konzultacije.
Dakle, supstitucija koja je potrebna za ovaj zadatak je v=x-u. Može i u-x ali je onda multiplikator malo kompliciraniji.
(iako sam i to doma napravio, ali iz nekog razloga sam zabrljao :) )
U jednadžbi
[latex]
\varphi(v)=\frac{\frac{df1}{du} - \frac{df2}{dx}}{\frac{dv}{dx}f2-\frac{dv}{du}f1}
[/latex]
brojnik već smo izračunali (to je A).
Sada gledamo:
[latex]
v=x-u\\
\frac{dv}{du}=-1 \\
\frac{dv}{dx}=1 \\
[/latex]
Računamo nazivnik:
[latex]
\frac{dv}{dx}f2-\frac{dv}{du}f1 = \\ u^2+u-2xu+x^2 - (-1)(-u) = \\ u^2+u-2xu+x^2-u=u^2-2xu+x^2=(u-x)^2\\[/latex]
[latex]
\varphi(x)=\frac{-1+2(u-x)}{(u-x)^2}=\frac{-1+2v}{v^2}=\frac{-1}{v^2}+\frac{2}{v}\\
\frac{1}{\mu}d\mu=\frac{-1}{v^2}dv+\frac{2}{v}dv\\[/latex]
[latex]
\ln{|\mu|}=\frac{1}{v}+2\ln{|v|}+C=\frac{1}{v}+\ln{v^2}+C, \quad C \in \mathbb{R} \\
\ln{|\mu|}=\ln{e^{\frac{1}{v}}}+\ln{v^2}+\ln{C}, \quad C \in \mathbb{R}\\
\mu=Ce^{\frac{1}{v}}v^2, \quad C \in \mathbb{R}
[/latex]
treba nam samo jedan multiplikator pa možemo uzeti C=1
[latex]\mu=e^{\frac{-1}{v}}v^2 \\
\mu=e^{\frac{1}{x-e^y}}(x-e^y)^2 \\
[/latex]
E sad provjeriti da li će dalje biti egzaktna jednadžba mi se neda trenutno, to ću kada dođem doma, ali mislim da bi trebalo sve biti dobro, samo što je malo ružan račun. Čudno kako su ovaj stavili jer oduzme preko pola sata ako se od početka zna što se radi, osim ako nema neki kraći put. :)
| koryanshea (napisa): |
2. zadatak iz proslogodisnjeg 2. kolokvija (jedna od 4 grupe):
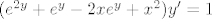 |
Nakon uvođenja substitucije
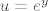 i jednadžbe i jednadžbe 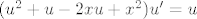 imaš dalje ovo: imaš dalje ovo:
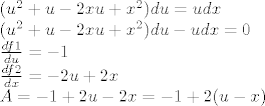
Sad nakon što sam razbijao glavu sa šablonama i supstitucijama koje su se radile na vježbama, odlučio sam odustati od zadatka i otići na konzultacije.
Dakle, supstitucija koja je potrebna za ovaj zadatak je v=x-u. Može i u-x ali je onda multiplikator malo kompliciraniji.
(iako sam i to doma napravio, ali iz nekog razloga sam zabrljao  ) )
U jednadžbi
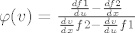
brojnik već smo izračunali (to je A).
Sada gledamo:
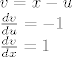
Računamo nazivnik:
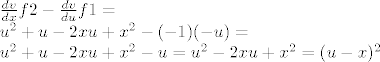
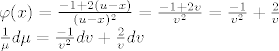
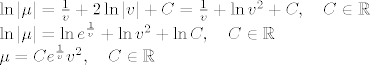
treba nam samo jedan multiplikator pa možemo uzeti C=1
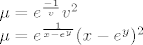
E sad provjeriti da li će dalje biti egzaktna jednadžba mi se neda trenutno, to ću kada dođem doma, ali mislim da bi trebalo sve biti dobro, samo što je malo ružan račun. Čudno kako su ovaj stavili jer oduzme preko pola sata ako se od početka zna što se radi, osim ako nema neki kraći put. 
_________________
The Dude Abides
|
|
| [Vrh] |
|
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
|
| [Vrh] |
|
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
 Postano: 23:09 sri, 1. 2. 2006 Naslov: Postano: 23:09 sri, 1. 2. 2006 Naslov: |
    |
|
|
evo jos par zadataka...
prvi sam rijesila skoro do kraja, i njegov problem nije "ne znam odakle da pocnem" nego "kretenski integral koji komplicira stvar vise nego je humano". tako da ovdje ne trazim pomoc nego kukam o nepravdi. i ucim latex :) slobodno preskocite.
1. zadatak, pismeni 4.2.2004.
Cauchyeva zadaća:
[latex]x''cosx+x'^2sinx=x'[/latex]
[latex]x(-1)=0[/latex]:nosmile:[latex]x'(-1)=2[/latex]
uvođenjem supstitucije x'=p(x) pa dijeljenjem s istim dobije se simpaticna rjesiva odj po x:
[latex]p'cosx+psinx=1[/latex]
dijeljenjem s cos x se dobije linearna, rijesimo homogenu, partikularno rjesenje je preocito sinx, uvrstimo uvjet, dobijemo
[latex]p(x)=sinx+2cosx[/latex]
međutim, p(x)=x'
dakle
[latex]dx/dt=sinx+2cosx[/latex]
[latex]dx/{(sinx+2cosx)}=dt[/latex]
integriranjem dobijemo nelijepo cudoviste
[latex]\displaystyle \ln\tan\left(\frac{x+\Theta}{2}\right)=\sqrt{5}t+\ln c[/latex]
gdje je [latex]\Theta[/latex] [i]nesto[/i] cega znamo sto je sinus, a sto tangens (tako pise u bronstejnu). uvrstavanjem uvjeta dobijemo
[latex]\tan \frac{\Theta}{2}=ce^{-\sqrt 5}[/latex]
kemijanjem po zbrojevima, umnoscima i kvadratima sinusova, kosinusova i sve njihove djece nisam uspjela dobit nista. i sad vi meni recite... da l' da se ljutim zbog potrosenih sati? gdje su oni ljudi sto su to rjesavali na pismenom?
drugi zadatak.... isti pismeni :!:
[latex]t^2x''+tx'-4x=t^2(12(\ln t)^2+6\ln t)[/latex]
pise: UPUTA: uvedite supstituciju [latex]t=e^u[/latex]
e sad mene zanima... je li se akademske godine 2003./2004. na ODJ radilo rjesavanje linearnih odj viseg reda sa NE NUZNO KONSTANTNIM koeficijentima? jer... nakon sati i sati provedenih nad ovim zadatkom, kemijanjem sa totalnim diferencijalima i svim ostalim potencijalnim metodama snizenja reda, sa predlozenom supstitucijom i bez nje, nisam nista postigla. onda je jedan drugi mozak poceo kopat po bronstajnu i nasao linearne odj viseg reda... a ova savrseno odgovara opisu :) a mi to uopce nismo radili na vjezbama... pa nek me netko pliz utjesi... da ja tako nesto necu vidit na pismenom... i da postoji dobro opravdanje zasto je taj zadatak tu... ili da postoji neka druga metoda...
hvala svima koji citaju moje placke :)
evo jos par zadataka...
prvi sam rijesila skoro do kraja, i njegov problem nije "ne znam odakle da pocnem" nego "kretenski integral koji komplicira stvar vise nego je humano". tako da ovdje ne trazim pomoc nego kukam o nepravdi. i ucim latex  slobodno preskocite. slobodno preskocite.
1. zadatak, pismeni 4.2.2004.
Cauchyeva zadaća:
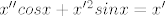
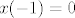  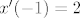
uvođenjem supstitucije x'=p(x) pa dijeljenjem s istim dobije se simpaticna rjesiva odj po x:
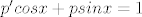
dijeljenjem s cos x se dobije linearna, rijesimo homogenu, partikularno rjesenje je preocito sinx, uvrstimo uvjet, dobijemo
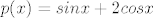
međutim, p(x)=x'
dakle
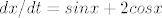
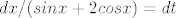
integriranjem dobijemo nelijepo cudoviste
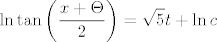
gdje je 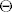 nesto cega znamo sto je sinus, a sto tangens (tako pise u bronstejnu). uvrstavanjem uvjeta dobijemo nesto cega znamo sto je sinus, a sto tangens (tako pise u bronstejnu). uvrstavanjem uvjeta dobijemo
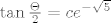
kemijanjem po zbrojevima, umnoscima i kvadratima sinusova, kosinusova i sve njihove djece nisam uspjela dobit nista. i sad vi meni recite... da l' da se ljutim zbog potrosenih sati? gdje su oni ljudi sto su to rjesavali na pismenom?
drugi zadatak.... isti pismeni 
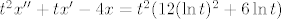
pise: UPUTA: uvedite supstituciju 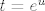
e sad mene zanima... je li se akademske godine 2003./2004. na ODJ radilo rjesavanje linearnih odj viseg reda sa NE NUZNO KONSTANTNIM koeficijentima? jer... nakon sati i sati provedenih nad ovim zadatkom, kemijanjem sa totalnim diferencijalima i svim ostalim potencijalnim metodama snizenja reda, sa predlozenom supstitucijom i bez nje, nisam nista postigla. onda je jedan drugi mozak poceo kopat po bronstajnu i nasao linearne odj viseg reda... a ova savrseno odgovara opisu  a mi to uopce nismo radili na vjezbama... pa nek me netko pliz utjesi... da ja tako nesto necu vidit na pismenom... i da postoji dobro opravdanje zasto je taj zadatak tu... ili da postoji neka druga metoda... a mi to uopce nismo radili na vjezbama... pa nek me netko pliz utjesi... da ja tako nesto necu vidit na pismenom... i da postoji dobro opravdanje zasto je taj zadatak tu... ili da postoji neka druga metoda...
hvala svima koji citaju moje placke 
_________________  "Download the files to a non-networked, firewalled computer."
- Dr. Elizabeth Weir |
|
| [Vrh] |
|
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
|
| [Vrh] |
|
|










