|
[quote="Anonymous"]Molim dobru dušu koja zna izračunati ova dva zadatka da mi pomogne.
1.) Neka je DcR^2 prirodno područje definicije f-je f(x,y)=sqrt(-x^2-y^2+2x) + sqrt(-x^2-y^2+6x-4). Naći površinu od D. Kada sve to redim dobijem (x-2)^2+y^2 =<4 i (x-3)^2+6y^2=<5 i dalje neznam probala sam uvesti posebno za svaku nejednadžbu uvesti supstitucije u=x-2 i v=y i izračunala i posebno za u=x-3 i v=y ali to mi baš i neispadne kako spada, bilo kako bilo neznam i drugi zadatak se tiče ekstrema
2.) U elipsoid x^2+y^2\4+z^2\9=1 upisati u tetraedar maksimalnog volumena čija su tri vrha A(0,0,1), B(0,-2,0) i C(0,0,3).[/quote]
U nedostatku inspiracije, mozes izracunat tocke presijeka dviju kruznica (btw, malo si krivo dobila uvjete),
[latex](x-1)^2+y^2 = 1 \\
(x-3)^2+y^2 = 5 \\
\Rightarrow x = 1, y^2 = 1[/latex]
Ako imas skicu, vidjet ces da je rjesenje od
[latex]\displaystyle \int_D 1 dxdy = 2 \int_0^1 \left( \int_{3^-\sqrt{5 - y^2}}^1 1dx \right) dy + 2 \int_0^2 \left( \int_1^{1 + \sqrt{1 - y^2}} 1dx \right) dy[/latex]
(lijevi integral ti je omeden sa vecom kruznicom, x osi i tetivom koja spaja presjeke kruznica, a desno je omeden sa malom kruznicom, x osi i tetivom.
Za drugi zadatak dobro dode da je volumen tetraedra odredenog sa tri vektora jednak sestini volumena paralelepipeda odredanog sa ta tri vektora. Recimo da vektore racunas iz tocke A:
[latex]a_1 = [0, -2, -1] \\
a_2 = [0, 0, 2] \\
a_3 = [x, y, z-1]
[/latex]
Povrsina parelelepipeda je apsolutna vrijednost determinante matrice koja sadrzi ta tri vektora, pa je povrsina tetraedra
[latex]V = \frac{|4x|}{6}[/latex]
[latex]|x| = \sqrt{x^2}[/latex], a drugi korijen je stropgo rastuca funkcija, pa se maksimum volumena postize u istoj tocki u kojoj se postize maksimum funkcije [latex]x^2[/latex]
Nas uvjet kaze [latex]x^2 = 1 - \frac{y^2}{4} - \frac{z^2}{9}[/latex]
Ocito je maksimum od [latex]x^2 = 1[/latex], znaci, maksimalan volumen tetraedra se postize u tockama
[latex]T_1 = (1, 0, 0) \\
T_2 = (-1, 0, 0)[/latex]
| Anonymous (napisa): | Molim dobru dušu koja zna izračunati ova dva zadatka da mi pomogne.
1.) Neka je DcR^2 prirodno područje definicije f-je f(x,y)=sqrt(-x^2-y^2+2x) + sqrt(-x^2-y^2+6x-4). Naći površinu od D. Kada sve to redim dobijem (x-2)^2+y^2 =<4 i (x-3)^2+6y^2=<5 i dalje neznam probala sam uvesti posebno za svaku nejednadžbu uvesti supstitucije u=x-2 i v=y i izračunala i posebno za u=x-3 i v=y ali to mi baš i neispadne kako spada, bilo kako bilo neznam i drugi zadatak se tiče ekstrema
2.) U elipsoid x^2+y^2\4+z^2\9=1 upisati u tetraedar maksimalnog volumena čija su tri vrha A(0,0,1), B(0,-2,0) i C(0,0,3). |
U nedostatku inspiracije, mozes izracunat tocke presijeka dviju kruznica (btw, malo si krivo dobila uvjete),
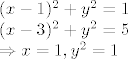
Ako imas skicu, vidjet ces da je rjesenje od
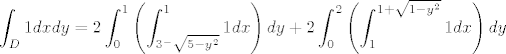
(lijevi integral ti je omeden sa vecom kruznicom, x osi i tetivom koja spaja presjeke kruznica, a desno je omeden sa malom kruznicom, x osi i tetivom.
Za drugi zadatak dobro dode da je volumen tetraedra odredenog sa tri vektora jednak sestini volumena paralelepipeda odredanog sa ta tri vektora. Recimo da vektore racunas iz tocke A:
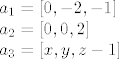
Povrsina parelelepipeda je apsolutna vrijednost determinante matrice koja sadrzi ta tri vektora, pa je povrsina tetraedra
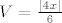
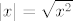 , a drugi korijen je stropgo rastuca funkcija, pa se maksimum volumena postize u istoj tocki u kojoj se postize maksimum funkcije 
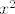
Nas uvjet kaze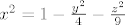 
Ocito je maksimum od 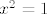 , znaci, maksimalan volumen tetraedra se postize u tockama
_________________
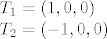
Bri
|
