| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 13:33 čet, 9. 2. 2006 Naslov: |
    |
|
|
Prije postavljanja pitanja, pristojno je malo potraziti. :roll: Recimo, prvi zadatak je [url=http://degiorgi.math.hr/forum/viewtopic.php?p=27608#27608]Tonci odgovorio prije skoro godinu dana[/url]. 8) Drugi mislim da je odgovoren s kruznicama (umjesto elipsa), no ne vidim u cemu bi bila razlika. :| Treci je takodjer negdje odgovoren (trazi malo i sam(a)). :)
Prije postavljanja pitanja, pristojno je malo potraziti.  Recimo, prvi zadatak je Tonci odgovorio prije skoro godinu dana.  Drugi mislim da je odgovoren s kruznicama (umjesto elipsa), no ne vidim u cemu bi bila razlika.  Treci je takodjer negdje odgovoren (trazi malo i sam(a)). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Grga
Forumaš(ica)
Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
| Postano: 13:53 čet, 9. 2. 2006 Naslov: |
|
|
|
Sto se drugog zadatka tice, dvije se elipse mogu sijeci u najvise 4 tocke. Ako imamo elipsu i napravimo jos jednu elipsu koja je sijece u 4 tocke, dobivamo jos cetiri "komada" ravnine, omedena dijelom nove elipse koji spaja pojedine dvije tocke i dijelom "stare" elipse. AKo otprije imas vise elipsi, nova svaku sijece u 4 tocke i za svaku od prijasnjih elipsi dobivas 4 nova dijela. (napravi si skicu pa ce biti jasnije) Ako sa [latex]a_n[/latex] oznacimo broj takvih podjela za n elipsi, tada je:
[latex]a_{n+1} = a_n + 4^n \\
a_1 = 2 \\
\Longrightarrow a_n = \frac{4^n - 1}{3} + 1[/latex]
Sto se drugog zadatka tice, dvije se elipse mogu sijeci u najvise 4 tocke. Ako imamo elipsu i napravimo jos jednu elipsu koja je sijece u 4 tocke, dobivamo jos cetiri "komada" ravnine, omedena dijelom nove elipse koji spaja pojedine dvije tocke i dijelom "stare" elipse. AKo otprije imas vise elipsi, nova svaku sijece u 4 tocke i za svaku od prijasnjih elipsi dobivas 4 nova dijela. (napravi si skicu pa ce biti jasnije) Ako sa 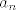 oznacimo broj takvih podjela za n elipsi, tada je:
_________________
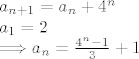
Bri
|
|
| [Vrh] |
|
Tina......
Gost
|
|
| [Vrh] |
|
Grga
Forumaš(ica)
Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol:
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Maroje
Forumaš(ica)
Pridružen/a: 20. 03. 2003. (08:49:56)
Postovi: (8F)16
|
| Postano: 15:27 ned, 30. 4. 2006 Naslov: |
|
|
|
[quote="Anonymous"]
odredite koeficijent uz x^q u razvoju polinoma
p(x)=suma(po i=0 do q)x^i * (x+1)^(p-i) , pri cemu je p>=q; p,q prirodni brojevi. (cijeli izraz je pod sumom)
to je konkretno bio drugi zadatak na zadnjem pismenom, pa ako bi netko znao puno bi mi pomogao!
[/quote]
Ne da mi se raspisivati osim ako Vam nije jako hitno. Rješenja možete naći u skriptarnici od utorka nadalje.
Pozdrav,
Maroje
P.S. Ako sami želite probati raspišite (x+1)^{p-i} prema binomnom teoremu, odredite koeficijente koji dolaze uz x^q i onda primijenite
pravilo gornje sumacije.
| Anonymous (napisa): |
odredite koeficijent uz x^q u razvoju polinoma
p(x)=suma(po i=0 do q)x^i * (x+1)^(p-i) , pri cemu je p>=q; p,q prirodni brojevi. (cijeli izraz je pod sumom)
to je konkretno bio drugi zadatak na zadnjem pismenom, pa ako bi netko znao puno bi mi pomogao!
|
Ne da mi se raspisivati osim ako Vam nije jako hitno. Rješenja možete naći u skriptarnici od utorka nadalje.
Pozdrav,
Maroje
P.S. Ako sami želite probati raspišite (x+1)^{p-i} prema binomnom teoremu, odredite koeficijente koji dolaze uz x^q i onda primijenite
pravilo gornje sumacije.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|
