|
[quote="lara"]Da li mi zna netko rješiti i objasniti ovaj zadatak. Naći točku na plohi
z-2=x^2+y^2 sa svojstvom da normala na plohu u toj točki bude paralelna ravninama 2x+y-z=3 i x-y+3z=9.[/quote]
Trazis tocku u kojoj je vektor normale na tangencijalnu ravninu zadane plohe okomit na vektore nornale zadanih dviju ravnina.
Gledas [latex]F = x^2 + y^2 - z + 2[/latex]
[latex]\nabla F(T_0) = (2 x_0, 2 y_0, -1) \\
n_1 = (2, 1, -1)\\
n_2 = (1, -1, 3)[/latex]
Ova zadnja dva vektora moraju biti okomiti na prvi, pa njihov skalarni produkt mroa biti nula:
[latex]4 x_0 + 2 y_0 +1 = 0 \\
2 x_0 - 2 y_0 -3 = 0\\
\Longrightarrow 6 x_0 = 2 \Rightarrow x_0 = \frac{1}{3} \Rightarrow y_0 = -\frac{7}{6}[/latex]
Sad trazis tocku na plohi koja to zadovoljava:
[latex]F(T_0) = \frac{1}{9} + \frac{49}{36} - z_0 +2 (=0) \\
\Rightarrow z_0 = \frac{125}{36}\\
T_0=\left( \frac{1}{3}, -\frac{7}{6}, \frac{125}{36} \right)[/latex]
| lara (napisa): | Da li mi zna netko rješiti i objasniti ovaj zadatak. Naći točku na plohi
z-2=x^2+y^2 sa svojstvom da normala na plohu u toj točki bude paralelna ravninama 2x+y-z=3 i x-y+3z=9. |
Trazis tocku u kojoj je vektor normale na tangencijalnu ravninu zadane plohe okomit na vektore nornale zadanih dviju ravnina.
Gledas 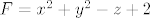
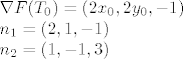
Ova zadnja dva vektora moraju biti okomiti na prvi, pa njihov skalarni produkt mroa biti nula:
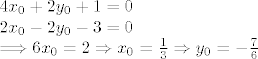
Sad trazis tocku na plohi koja to zadovoljava:
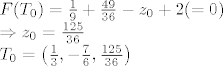
_________________
Bri
|





