|
[quote="Mojo"]e ovako. u jednom zadatku racunam diferenijabilnost tj. ispitujem da li je "dobar" diferencijal kojeg sam dobio preko parcijalnih derivacija. i dobije se u nekom koraku:
[latex]\lim_{(h_1,h_2) \to 0}\frac{h_1^{2} \sin(\frac{1}{h_1}) + h_2^{2}}{\sqrt{h_1^{2} + h_2^{2}}}[/latex]
e i sad to je 0/0 a zadatak kaze da taj izraz ide u 0. a meni to bas nije jasno. ocito je neka standardna stvar koju ja nevidin, jer jos u par zadataka koje san rjesava imam isti problem sa 0/0.
ako neko zna, bio bih vrlo zahvalan[/quote]
Tu samo moras malo ocijeniti, za [latex](h_1,h_2)\neq (0,0)[/latex] imamo nejednakost
[latex]0 \leq\frac{|h_1^{2} \sin(\frac{1}{h_1}) + h_2^{2}|}{\sqrt{h_1^{2} + h_2^{2}}}
\leq \frac{h_1^{2} |\sin(\frac{1}{h_1})| + h_2^{2}}{\sqrt{h_1^{2} + h_2^{2}}} \leq \frac{h_1^{2} + h_2^{2}}{\sqrt{h_1^{2} + h_2^{2}}}=\sqrt{h_1^{2} + h_2^{2}}. [/latex]
(prva nejednakost je nejednakost trokuta, a druga vrijedi zato jer je [latex]|\sin x|\leq 1, \ \forall x \in \mathbb{R} [/latex]). Desna strana u toj ocjeni predstavlja neprekidnu funkciju ([latex](h_1,h_2) \mapsto \sqrt{h_1^2+h_2^2}[/latex]) čija je vrijednost u [latex]0[/latex] jednaka [latex]0[/latex] (što povlači da je i njen limes u [latex]0[/latex] jednak [latex]0[/latex]), pa iz teorema o sendviču slijedi da je [latex]\lim_{(h_1,h_2) \to 0}\frac{h_1^{2} \sin(\frac{1}{h_1}) + h_2^{2}}{\sqrt{h_1^{2} + h_2^{2}}}=0[/latex]
| Mojo (napisa): | e ovako. u jednom zadatku racunam diferenijabilnost tj. ispitujem da li je "dobar" diferencijal kojeg sam dobio preko parcijalnih derivacija. i dobije se u nekom koraku:
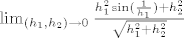
e i sad to je 0/0 a zadatak kaze da taj izraz ide u 0. a meni to bas nije jasno. ocito je neka standardna stvar koju ja nevidin, jer jos u par zadataka koje san rjesava imam isti problem sa 0/0.
ako neko zna, bio bih vrlo zahvalan |
Tu samo moras malo ocijeniti, za 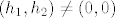 imamo nejednakost imamo nejednakost
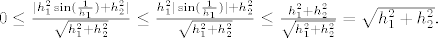
(prva nejednakost je nejednakost trokuta, a druga vrijedi zato jer je 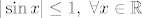 ). Desna strana u toj ocjeni predstavlja neprekidnu funkciju ( ). Desna strana u toj ocjeni predstavlja neprekidnu funkciju (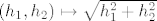 ) čija je vrijednost u ) čija je vrijednost u  jednaka jednaka  (što povlači da je i njen limes u (što povlači da je i njen limes u  jednak jednak  ), pa iz teorema o sendviču slijedi da je ), pa iz teorema o sendviču slijedi da je 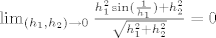
|




