|
[quote="Anonymous"]ilja jel bi te mogao samo zamoliti da mi ukratko samo napises(idejno) kako bi se tebala rijesiti ova 3 zadatka s roka u 12 mj.(ili mozda netko tko je bio na tom roku.)hvala
1.zad:funkciju f:[1,3] u R zadanu formulom f(x)=arctg(X)
aprox linearnim splinom pn na ekvidistantnoj mrezi s n+1 cvorova na tom segmentu.oznacimo s n(epsilon) najmanji n takav da ocjena unif pogreske apox fije splineom pn na segmentu ne prelazi 10 na -4.odredite(nepsilon) i izracunajte pn(epsilon)(1.95).
3.onaj sa infimumom skupa
4.ideja?[/quote]
Možeš :)
[b]1.[/b] Kako je funkcija f klase [latex]C^2([1,3])[/latex], ocjena uniformne pogreške (imate ju u vježbama) je dana sa [latex] \|f(x)-p_n(x)\|_\infty^{[1,3]}\leq \frac{1}{8}h_n^2 \cdot M_2f [/latex],
gdje je [latex]h_n=\frac{3-1}{n}=\frac{2}{n}[/latex] očica n-te ekvidistantne subdivizije segmenta [latex][1,3][/latex] i standardno [latex]M_2f= \|f''\|_\infty^{[1,3]}[/latex].
Znači, za [latex]\varepsilon:=10^{-4}[/latex] treba naći najmanji [latex]n \in \mathbb{N}[/latex] za kojeg je [latex] \frac{1}{8}h_n^2 \cdot M_2f < \varepsilon[/latex].
Još moraš odrediti [latex]M_2f[/latex], a to je jednostavno, deriviraš triput funkciju f, rješiš jednadžbu [latex]f'''(x)=0[/latex], dobiješ stacionarne točke od [latex]f''[/latex], redom ih uvrstiš u [latex]f''[/latex] i ne zaboraviš provjeriti vrijednosti od [latex]f''[/latex] u rubovima segmenta (tj. u točkama 1 i 3). Po modulu najveća od tih vrijednosti je upravo [latex]M_2f[/latex]. Mislim da se dobije [latex]n_0=50[/latex] (samo mislim). Ako je tako, na kraju primijetiš da se [latex]1.95[/latex] nalazi u 24. podintervalu te subdivizije segmenta [latex][1,3][/latex] (na 50 podintervale), tj. da je [latex]1.95 \in [1.92,1.96] (=[1+23\cdot\frac{2}{50}, 1+24\cdot\frac{2}{50}])[/latex] i konstruiraš linearni spline na tom podintervalu i izračunaš njegovu vrijednost u točki [latex]1.95[/latex].
[b]3.[/b] Primijeti da je
[latex]\inf \Big\{\lambda \in \mathbb{R} : \ e^{-\lambda x} \leq \frac{1}{1+x^2} \quad \forall x \in \mathbb{R}_+ \Big\}=\inf \Big\{\lambda \in \mathbb{R} : \ \lambda \geq \frac{\ln(1+x^2)}{x} \quad \forall x \in \mathbb{R}_+ \Big\}[/latex].
Dakle, s točnošću [latex]\varepsilon :=5\cdot 10^{-3}[/latex] treba odrediti maksimum funkcije [latex]f(x):=\frac{\ln(1+x^2)}{x}[/latex] na [latex]\mathbb{R}_+[/latex] (tu trebate pokazati da je zaista riječ o maksimumu, tj. da funkcija poprima globalni maksimum na [latex]\mathbb{R}_+[/latex], a za to morate analizirati danu funkciju (gradivo MA2)).
[b]4.[/b] Najprije primijeti da je [latex]\mathrm{sgn}\bigg[\arcsin \bigg(\frac{x}{2006}\bigg)\bigg]=\mathop{\mathrm{sgn}}x, \ \forall x \in [-2005,2006][/latex] i da je podintegralna funkcija neparna. Zato je
[latex]I:=\int_{-2005}^{2006}e^{-(|x|-2005)^2}\cdot \mathrm{sgn}\bigg[\arcsin \bigg(\frac{x}{2006}\bigg)\bigg]~dx=\int_{2005}^{2006}e^{-(|x|-2005)^2}~dx=[/latex][latex]\int_{2005}^{2006}e^{-(x-2005)^2}~dx[/latex].
Nakon toga napravimo supstituciju [latex]t:=x-2005[/latex], pa dobijemo
[latex]I=\int_{0}^{1}e^{-t^2}~dt[/latex],
a dalje ide numerika, tj. dani integral izračunate nekom metododm numeričke integracije (npr. produljenom trapeznom formulom).
| Anonymous (napisa): | ilja jel bi te mogao samo zamoliti da mi ukratko samo napises(idejno) kako bi se tebala rijesiti ova 3 zadatka s roka u 12 mj.(ili mozda netko tko je bio na tom roku.)hvala
1.zad:funkciju f:[1,3] u R zadanu formulom f(x)=arctg(X)
aprox linearnim splinom pn na ekvidistantnoj mrezi s n+1 cvorova na tom segmentu.oznacimo s n(epsilon) najmanji n takav da ocjena unif pogreske apox fije splineom pn na segmentu ne prelazi 10 na -4.odredite(nepsilon) i izracunajte pn(epsilon)(1.95).
3.onaj sa infimumom skupa
4.ideja? |
Možeš 
1. Kako je funkcija f klase 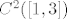 , ocjena uniformne pogreške (imate ju u vježbama) je dana sa , ocjena uniformne pogreške (imate ju u vježbama) je dana sa 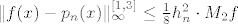 , ,
gdje je 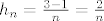 očica n-te ekvidistantne subdivizije segmenta očica n-te ekvidistantne subdivizije segmenta 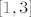 i standardno i standardno 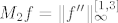 . .
Znači, za 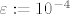 treba naći najmanji treba naći najmanji  za kojeg je za kojeg je 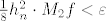 . .
Još moraš odrediti 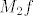 , a to je jednostavno, deriviraš triput funkciju f, rješiš jednadžbu , a to je jednostavno, deriviraš triput funkciju f, rješiš jednadžbu 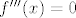 , dobiješ stacionarne točke od , dobiješ stacionarne točke od  , redom ih uvrstiš u , redom ih uvrstiš u  i ne zaboraviš provjeriti vrijednosti od i ne zaboraviš provjeriti vrijednosti od  u rubovima segmenta (tj. u točkama 1 i 3). Po modulu najveća od tih vrijednosti je upravo u rubovima segmenta (tj. u točkama 1 i 3). Po modulu najveća od tih vrijednosti je upravo 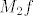 . Mislim da se dobije . Mislim da se dobije 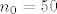 (samo mislim). Ako je tako, na kraju primijetiš da se (samo mislim). Ako je tako, na kraju primijetiš da se 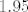 nalazi u 24. podintervalu te subdivizije segmenta nalazi u 24. podintervalu te subdivizije segmenta 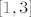 (na 50 podintervale), tj. da je (na 50 podintervale), tj. da je 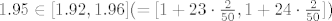 i konstruiraš linearni spline na tom podintervalu i izračunaš njegovu vrijednost u točki i konstruiraš linearni spline na tom podintervalu i izračunaš njegovu vrijednost u točki 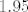 . .
3. Primijeti da je
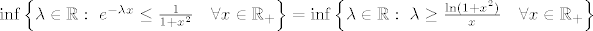 . .
Dakle, s točnošću 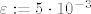 treba odrediti maksimum funkcije treba odrediti maksimum funkcije 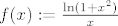 na na 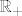 (tu trebate pokazati da je zaista riječ o maksimumu, tj. da funkcija poprima globalni maksimum na (tu trebate pokazati da je zaista riječ o maksimumu, tj. da funkcija poprima globalni maksimum na 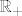 , a za to morate analizirati danu funkciju (gradivo MA2)). , a za to morate analizirati danu funkciju (gradivo MA2)).
4. Najprije primijeti da je 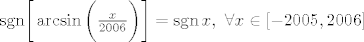 i da je podintegralna funkcija neparna. Zato je i da je podintegralna funkcija neparna. Zato je
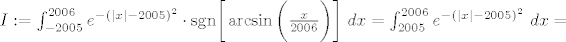 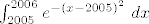 . .
Nakon toga napravimo supstituciju 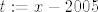 , pa dobijemo , pa dobijemo
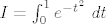 , ,
a dalje ide numerika, tj. dani integral izračunate nekom metododm numeričke integracije (npr. produljenom trapeznom formulom).
|





