bok! ta supstitucija ti definitivno ne pomaze jer onda dobijes koja sadrzi [b]i[/b] x, [b]i[/b] y, [b]i[/b] p, pa nisi nista postigao.
ta odj je ono sto se zove "poopcena homogena";
napomena: ako si ove godine slusao ODJ mozda se to nije radilo na vjezbama, pa ti nece bit ni na pismenom.
dakle, u jdbu umjesto x uvrstimo kx
umjesto y -> [latex]k^m y[/latex]
umjesto y' -> [latex]k^{m-1} y'[/latex]
i pitamo se - postoji li cijeli broj m takav da mozemo pokratit k-ove nakon gornjeg uvrstavanja
[latex]y=2xy´+ \frac {1} {y´^2}[/latex]
[latex]k^my=kk^{m-1}2xy´+ \frac {k^{-2(m-1)}} {y´^2}[/latex]
dakle trazimo m takav da mozemo podijeliti jdbu sa [latex]k^{nesto}[/latex] i dobit pocetnu ODJ
[latex]m=1+m-1=-2(m-1)[/latex]
[latex]m=-2m+2 => m=3/2[/latex]
odj se rjesava supstitucijama:
[latex]x=e^t \ \ t=lnx \ \ dt/dx=1/x=\frac {1}{e^t}=e^{-t} \\
y=ze^{mt}[/latex] gdje je z=z(t)
pa je [latex]y'=z't'e^{mt}+mze^{mt}t' \\
y'=e^{(m-1)t}(z'+mz)[/latex]
uvrsti, trebali bi ti se pokratit svi [latex]e^{nesto}[/latex] i jos svasta nesto bi se trebalo pokratit i sretno ;)
bok! ta supstitucija ti definitivno ne pomaze jer onda dobijes koja sadrzi i x, i y, i p, pa nisi nista postigao.
ta odj je ono sto se zove "poopcena homogena";
napomena: ako si ove godine slusao ODJ mozda se to nije radilo na vjezbama, pa ti nece bit ni na pismenom.
dakle, u jdbu umjesto x uvrstimo kx
umjesto y →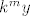 
umjesto y' →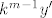 
i pitamo se - postoji li cijeli broj m takav da mozemo pokratit k-ove nakon gornjeg uvrstavanja
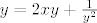
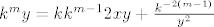
dakle trazimo m takav da mozemo podijeliti jdbu sa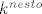 
i dobit pocetnu ODJ
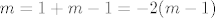
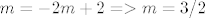
odj se rjesava supstitucijama:
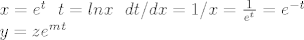gdje je z=z(t)
pa je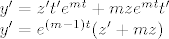 
uvrsti, trebali bi ti se pokratit svi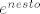 
i jos svasta nesto bi se trebalo pokratit i sretno 
_________________
"Download the files to a non-networked, firewalled computer."
- Dr. Elizabeth Weir
