| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
zeix
Forumaš(ica)

Pridružen/a: 18. 02. 2006. (12:39:11)
Postovi: (75)16
|
 Postano: 14:16 pon, 27. 2. 2006 Naslov: Pomoc u vezi zadatka iz domaceg Postano: 14:16 pon, 27. 2. 2006 Naslov: Pomoc u vezi zadatka iz domaceg |
    |
|
|
Ako neki od asistenata iz TAF-a (znam da vas je puno, pa ce neko sigurno pomoc :) ) moze pomoci i malo razbijat glavu evo jedan smisan zadacic. Svaki komentar u vezi rijesenja je dobrodosao.
Neka je [latex]f: \mathbb{C}\rightarrow W[/latex] natkrivanje koje nije izomorfizam Riemannovih ploha. Dokažite da tada vrijedi jedna od sljedeće dvije mogućnosti:
[list](a) Postoji [latex]b \in \mathbb{C}^{*}[/latex] takav da je [latex]\tau (f) = \left\{ \phi _{nb}; n \in \mathbb{Z}\right\} [/latex]. U tom slučaju Riemannova ploha [latex]W[/latex] izomorfna je Riemannovoj plohi [latex]\mathbb{C}^{*}[/latex].
(b) Postoje [latex]b, c \in \mathbb{C}[/latex] koji su linearno zavisni nad [latex]\mathbb{R}[/latex], tj. [latex]\frac{b}{c} \notin \mathbb{R}[/latex], takvi da je [latex]\tau (f) = \left\{ \phi _{nb+mc}; n, m \in \mathbb{Z}\right\} [/latex]. Tada je ploha [latex]W[/latex] homeomorfna torusu [latex]S^{2} = S \times S = \left\{ (\lambda , \mu ); \vert \lambda \vert = \vert \mu \vert = 1\right\} [/latex].[/list:u]
[size=7]Go Ilja, Go[/size]
Ako neki od asistenata iz TAF-a (znam da vas je puno, pa ce neko sigurno pomoc  ) moze pomoci i malo razbijat glavu evo jedan smisan zadacic. Svaki komentar u vezi rijesenja je dobrodosao. ) moze pomoci i malo razbijat glavu evo jedan smisan zadacic. Svaki komentar u vezi rijesenja je dobrodosao.
Neka je 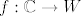 natkrivanje koje nije izomorfizam Riemannovih ploha. Dokažite da tada vrijedi jedna od sljedeće dvije mogućnosti: natkrivanje koje nije izomorfizam Riemannovih ploha. Dokažite da tada vrijedi jedna od sljedeće dvije mogućnosti:
(a) Postoji  takav da je takav da je 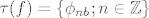 . U tom slučaju Riemannova ploha . U tom slučaju Riemannova ploha 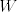 izomorfna je Riemannovoj plohi izomorfna je Riemannovoj plohi 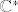 . .
(b) Postoje 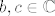 koji su linearno zavisni nad koji su linearno zavisni nad  , tj. , tj. 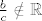 , takvi da je , takvi da je 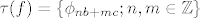 . Tada je ploha . Tada je ploha 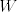 homeomorfna torusu homeomorfna torusu 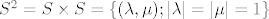 . .
Go Ilja, Go
_________________
"From this proposition it will follow, when arithmetical addition has been defined, that 1+1=2."
Page 360, Principia Mathematica
|
|
| [Vrh] |
|
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
|
| [Vrh] |
|
Exodus
Forumaš s poteškoćama u pisanju

Pridružen/a: 18. 11. 2002. (01:38:21)
Postovi: (1C)16
Spol: 
Sarma: -
Lokacija: MA1-4
|
 Postano: 17:03 uto, 28. 2. 2006 Naslov: Re: Pomoc u vezi zadatka iz domaceg Postano: 17:03 uto, 28. 2. 2006 Naslov: Re: Pomoc u vezi zadatka iz domaceg |
    |
|
|
[quote="zeix"]Ako neki od asistenata iz TAF-a (znam da vas je puno, pa ce neko sigurno pomoc :) ) moze pomoci i malo razbijat glavu evo jedan smisan zadacic. Svaki komentar u vezi rijesenja je dobrodosao.
Neka je [latex]f: \mathbb{C}\rightarrow W[/latex] natkrivanje koje nije izomorfizam Riemannovih ploha. Dokažite da tada vrijedi jedna od sljedeće dvije mogućnosti:
[list](a) Postoji [latex]b \in \mathbb{C}^{*}[/latex] takav da je [latex]\tau (f) = \left\{ \phi _{nb}; n \in \mathbb{Z}\right\} [/latex]. U tom slučaju Riemannova ploha [latex]W[/latex] izomorfna je Riemannovoj plohi [latex]\mathbb{C}^{*}[/latex].
(b) Postoje [latex]b, c \in \mathbb{C}[/latex] koji su linearno zavisni nad [latex]\mathbb{R}[/latex], tj. [latex]\frac{b}{c} \notin \mathbb{R}[/latex], takvi da je [latex]\tau (f) = \left\{ \phi _{nb+mc}; n, m \in \mathbb{Z}\right\} [/latex]. Tada je ploha [latex]W[/latex] homeomorfna torusu [latex]S^{2} = S \times S = \left\{ (\lambda , \mu ); \vert \lambda \vert = \vert \mu \vert = 1\right\} [/latex].[/list:u]
[size=7]Go Ilja, Go[/size][/quote]
Budući je Ilja pao u bed nakon što su ekskomunicirali Velikog Limuna, zadužio je mene vam se ukažem... :?
E pa sad, dat ću ti skicu:
Prvo, znamo da je [latex]\tau (f)[/latex] podgrupa grupe holomorfnih automorfizama [latex]\mathrm{Aut}(\mathbb{C})[/latex] od [latex]\mathbb{C}[/latex].
Na vježbama smo pokazali da je [latex]\mathrm{Aut}(\mathbb{C})=\{z \mapsto az+b : \ a \in \mathbb{C}^*, b \in \mathbb{C}\}[/latex].
E sad, ako je [latex]f: \mathbb{C}\rightarrow W[/latex] natkrivanje koje nije izomorfizam Riemannovih ploha tada je [latex]\tau (f)[/latex]
podgrupa grupe translacija [latex]T[/latex] na [latex]\mathbb{C}[/latex], (tj. [latex]T=\{\varphi_b : \mathbb{C} \rightarrow \mathbb{C}: \ \varphi_b(z)=z+b\} \cong \mathbb{C}[/latex]) i [latex]\tau (f)[/latex] djeluje diskontinuirano na [latex] \mathbb{C}[/latex], tj. svaka točka [latex]z \in \mathbb{C}[/latex] ima okolinu [latex]U_z[/latex] takvu da je za [latex]\varphi \in \tau (f) \setminus \{1\}[/latex] presjek [latex]U_z \cap \varphi (U_z)[/latex] prazan. Zato je [latex]\tau (f)[/latex] diskretna podgrupa od (aditivne grupe) [latex]\mathbb{C}[/latex], a takvih je samo dva tipa i to su one pod (a) i (b).
Srdačan pozdrav,
dr. Exodus :croatia:
| zeix (napisa): | Ako neki od asistenata iz TAF-a (znam da vas je puno, pa ce neko sigurno pomoc  ) moze pomoci i malo razbijat glavu evo jedan smisan zadacic. Svaki komentar u vezi rijesenja je dobrodosao. ) moze pomoci i malo razbijat glavu evo jedan smisan zadacic. Svaki komentar u vezi rijesenja je dobrodosao.
Neka je 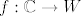 natkrivanje koje nije izomorfizam Riemannovih ploha. Dokažite da tada vrijedi jedna od sljedeće dvije mogućnosti: natkrivanje koje nije izomorfizam Riemannovih ploha. Dokažite da tada vrijedi jedna od sljedeće dvije mogućnosti:
(a) Postoji  takav da je takav da je 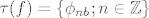 . U tom slučaju Riemannova ploha . U tom slučaju Riemannova ploha 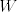 izomorfna je Riemannovoj plohi izomorfna je Riemannovoj plohi 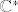 . .
(b) Postoje 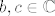 koji su linearno zavisni nad koji su linearno zavisni nad  , tj. , tj. 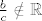 , takvi da je , takvi da je 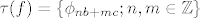 . Tada je ploha . Tada je ploha 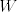 homeomorfna torusu homeomorfna torusu 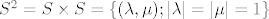 . .
Go Ilja, Go |
Budući je Ilja pao u bed nakon što su ekskomunicirali Velikog Limuna, zadužio je mene vam se ukažem... 
E pa sad, dat ću ti skicu:
Prvo, znamo da je 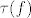 podgrupa grupe holomorfnih automorfizama podgrupa grupe holomorfnih automorfizama 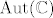 od od  . .
Na vježbama smo pokazali da je 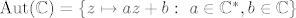 . .
E sad, ako je 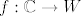 natkrivanje koje nije izomorfizam Riemannovih ploha tada je natkrivanje koje nije izomorfizam Riemannovih ploha tada je 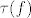
podgrupa grupe translacija  na na  , (tj. , (tj. 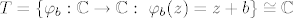 ) i ) i 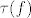 djeluje diskontinuirano na djeluje diskontinuirano na  , tj. svaka točka , tj. svaka točka 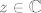 ima okolinu ima okolinu 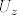 takvu da je za takvu da je za 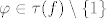 presjek presjek 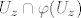 prazan. Zato je prazan. Zato je 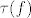 diskretna podgrupa od (aditivne grupe) diskretna podgrupa od (aditivne grupe)  , a takvih je samo dva tipa i to su one pod (a) i (b). , a takvih je samo dva tipa i to su one pod (a) i (b).
Srdačan pozdrav,
dr. Exodus 
|
|
| [Vrh] |
|
zeix
Forumaš(ica)

Pridružen/a: 18. 02. 2006. (12:39:11)
Postovi: (75)16
|
 Postano: 18:39 uto, 28. 2. 2006 Naslov: Postano: 18:39 uto, 28. 2. 2006 Naslov: |
    |
|
|
Cili taj text sta si napisa pise i meni prije zadatka, al je problem bija da ja nisam zna da postoje samo 2 diskretne podgrupe od C, niti uopce sta je diskretna grupa. Ipak se ovo zove Teorija Analitickih Funkcija, a ne teorija Grupa :) Ovo je pomoglo, sad jos moran skuzit ostatak zadatka (a i torus se ovdi prvi put spominje)
Cili taj text sta si napisa pise i meni prije zadatka, al je problem bija da ja nisam zna da postoje samo 2 diskretne podgrupe od C, niti uopce sta je diskretna grupa. Ipak se ovo zove Teorija Analitickih Funkcija, a ne teorija Grupa  Ovo je pomoglo, sad jos moran skuzit ostatak zadatka (a i torus se ovdi prvi put spominje) Ovo je pomoglo, sad jos moran skuzit ostatak zadatka (a i torus se ovdi prvi put spominje)
_________________
"From this proposition it will follow, when arithmetical addition has been defined, that 1+1=2."
Page 360, Principia Mathematica
|
|
| [Vrh] |
|
Exodus
Forumaš s poteškoćama u pisanju

Pridružen/a: 18. 11. 2002. (01:38:21)
Postovi: (1C)16
Spol: 
Sarma: -
Lokacija: MA1-4
|
 Postano: 20:05 uto, 28. 2. 2006 Naslov: Postano: 20:05 uto, 28. 2. 2006 Naslov: |
    |
|
|
Aha, nisam znao što te točno muči. :drinking:
Diskretna grupa je grupa snabdjevena diskretnom topologijom, tj. svaki podskup te grupe je otvoren. Budući [latex]\tau(f)[/latex] (kao podskup od [latex]\mathbb{C}[/latex]) nema gomilišta (u [latex]\mathbb{C}[/latex]), svakako je [latex]\tau(f)[/latex] diskretna.
Znači, najprije dokažeš da (do na izomorfizam) postoje samo dvije diskretne podgrupe od [latex]\mathbb{C}[/latex] i to su [latex]\mathbb{Z}[/latex] i [latex]\mathbb{Z}^2[/latex] (nije teško).
Možda ti još ovo pomogne u shvaćanju zadatka:
1. :drinking:
2. Ako je [latex]\tau(f)\cong \mathbb{Z}[/latex], to je (a) slučaj i budući je [latex]\tau(f)[/latex] izomorfna fundamentalnoj grupi [latex]\pi_1(W)[/latex] od [latex]W[/latex], pa je [latex]\pi_1(W) \cong\mathbb{Z}\cong \pi_1(S^1) \cong \pi_1(\mathbb{C}^*) [/latex] (kružnica [latex]S^1[/latex] i punktirana kompleksna ravnina [latex]\mathbb{C}^*[/latex] su istog homotopskog tipa).
Ako je pak [latex]\tau(f)\cong \mathbb{Z}^2[/latex], onda smo u (b) slučaju i [latex]\pi_1(W) \cong \tau(f)\cong \mathbb{Z}^2\cong \pi_1(S^1) \times \pi_1(S^1) \cong \pi_1(S^2) [/latex] (općenito za putovima povezane prostore [latex]X[/latex] i [latex]Y[/latex] vrijedi [latex]\pi_1(X \times Y) \cong \pi_1(X) \times \pi_1(Y) [/latex]).
Srdačan pozdrav,
dr. Exodus :croatia:
Aha, nisam znao što te točno muči. 
Diskretna grupa je grupa snabdjevena diskretnom topologijom, tj. svaki podskup te grupe je otvoren. Budući 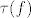 (kao podskup od (kao podskup od  ) nema gomilišta (u ) nema gomilišta (u  ), svakako je ), svakako je 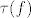 diskretna. diskretna.
Znači, najprije dokažeš da (do na izomorfizam) postoje samo dvije diskretne podgrupe od  i to su i to su 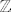 i i 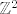 (nije teško). (nije teško).
Možda ti još ovo pomogne u shvaćanju zadatka:
1. 
2. Ako je 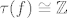 , to je (a) slučaj i budući je , to je (a) slučaj i budući je 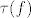 izomorfna fundamentalnoj grupi izomorfna fundamentalnoj grupi 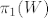 od od 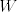 , pa je , pa je 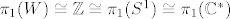 (kružnica (kružnica 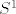 i punktirana kompleksna ravnina i punktirana kompleksna ravnina 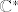 su istog homotopskog tipa). su istog homotopskog tipa).
Ako je pak 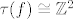 , onda smo u (b) slučaju i , onda smo u (b) slučaju i 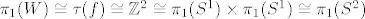 (općenito za putovima povezane prostore (općenito za putovima povezane prostore  i i 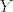 vrijedi vrijedi 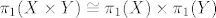 ). ).
Srdačan pozdrav,
dr. Exodus 
|
|
| [Vrh] |
|
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
|
| [Vrh] |
|
Exodus
Forumaš s poteškoćama u pisanju

Pridružen/a: 18. 11. 2002. (01:38:21)
Postovi: (1C)16
Spol: 
Sarma: -
Lokacija: MA1-4
|
|
| [Vrh] |
|
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
vjakovac
Forumaš s poteškoćama u pisanju

Pridružen/a: 28. 02. 2006. (10:07:16)
Postovi: (4B)16
|
|
| [Vrh] |
|
Exodus
Forumaš s poteškoćama u pisanju

Pridružen/a: 18. 11. 2002. (01:38:21)
Postovi: (1C)16
Spol: 
Sarma: -
Lokacija: MA1-4
|
 Postano: 23:32 uto, 28. 2. 2006 Naslov: Postano: 23:32 uto, 28. 2. 2006 Naslov: |
    |
|
|
[quote="Pericius"]Samo testiram dal' asistenti imaju smisao za humor. You passed the test! :wink:
Cheers![/quote]
A ne, ne, nemoj se sad izvlačit, htio si provjeriti da li ima šanse da ti budem cura. E pa nema, neda mi mama. :shock:
Bože moj, pa ovo je već off-topic, evo napišem jedan integral, pa da ispadne kak vodimo pametne rasprave:
[latex]\int_{0}^{1}\frac{1}{\sqrt{x(1-x)}}dx=\pi[/latex].
I reci ti meni, kako život, puši li se štogod? Malboro?
Srdačan pozdrav,
dr. Exodus :croatia:
| Pericius (napisa): | Samo testiram dal' asistenti imaju smisao za humor. You passed the test! 
Cheers! |
A ne, ne, nemoj se sad izvlačit, htio si provjeriti da li ima šanse da ti budem cura. E pa nema, neda mi mama. 
Bože moj, pa ovo je već off-topic, evo napišem jedan integral, pa da ispadne kak vodimo pametne rasprave:
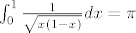 . .
I reci ti meni, kako život, puši li se štogod? Malboro?
Srdačan pozdrav,
dr. Exodus 
|
|
| [Vrh] |
|
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
 Postano: 23:42 uto, 28. 2. 2006 Naslov: Postano: 23:42 uto, 28. 2. 2006 Naslov: |
    |
|
|
Evo jedan i sa moje strane (integral, naravno). Cak ga necu ni TeX-irat, nego linkat na sliku.
[img]http://upload.wikimedia.org/math/4/2/9/429d5cc4a8b4fa1ada101cce1f631886.png[/img]
Marlboro? Ne hvala, prestajem. Trudim se bit ugledan clan akademske zajednice. Tesko je to, znas? :wink:
Evo jedan i sa moje strane (integral, naravno). Cak ga necu ni TeX-irat, nego linkat na sliku.

Marlboro? Ne hvala, prestajem. Trudim se bit ugledan clan akademske zajednice. Tesko je to, znas? 
_________________
Eat a lot, sleep a lot, brush 'em like crazy.
Run a lot, do a lot, never be lazy.
|
|
| [Vrh] |
|
Exodus
Forumaš s poteškoćama u pisanju

Pridružen/a: 18. 11. 2002. (01:38:21)
Postovi: (1C)16
Spol: 
Sarma: -
Lokacija: MA1-4
|
 Postano: 23:57 uto, 28. 2. 2006 Naslov: Postano: 23:57 uto, 28. 2. 2006 Naslov: |
    |
|
|
[quote="Pericius"]Evo jedan i sa moje strane (integral, naravno). Cak ga necu ni TeX-irat, nego linkat na sliku.
[img]http://upload.wikimedia.org/math/4/2/9/429d5cc4a8b4fa1ada101cce1f631886.png[/img]
Marlboro? Ne hvala, prestajem. Trudim se bit ugledan clan akademske zajednice. Tesko je to, znas? :wink:[/quote]
Hm. da, ali nije to baš jako teško, kada te stisne zapališ pljugu i otpjevaš ponosno neku koračnicu, npr. "Kad sam pušil zid sam bušil" i prođe. A šta sad, treba biti jak...
[latex]\lim_{R \rightarrow \infty}\int_{-R}^{R}\frac{x^3 \sin x}{(x^2+1)^2}dx=\frac{\pi}{2e}[/latex].
E, i tvoj integral malo šteka, pa nije baš da je uvijek konačan. Ali je možda zato život konačan? Hm.. :? Ma, :drinking:
Srdačan pozdrav,
dr. Exodus :croatia:
| Pericius (napisa): | Evo jedan i sa moje strane (integral, naravno). Cak ga necu ni TeX-irat, nego linkat na sliku.

Marlboro? Ne hvala, prestajem. Trudim se bit ugledan clan akademske zajednice. Tesko je to, znas?  |
Hm. da, ali nije to baš jako teško, kada te stisne zapališ pljugu i otpjevaš ponosno neku koračnicu, npr. "Kad sam pušil zid sam bušil" i prođe. A šta sad, treba biti jak...
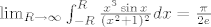 . .
E, i tvoj integral malo šteka, pa nije baš da je uvijek konačan. Ali je možda zato život konačan? Hm..  Ma, Ma, 
Srdačan pozdrav,
dr. Exodus 
|
|
| [Vrh] |
|
zeix
Forumaš(ica)

Pridružen/a: 18. 02. 2006. (12:39:11)
Postovi: (75)16
|
 Postano: 0:13 sri, 1. 3. 2006 Naslov: Postano: 0:13 sri, 1. 3. 2006 Naslov: |
    |
|
|
Hmm, vidim ja da vi stvarno nemate pametnijeg posla nego se zafrkajete po ovom topicu. Uz sve te silne i umne rasprave i kako zapravo je konacni integral smisao zivota, mogli bi meni jednostavno rijesit zadatak, a kako ocito imate vrimena na bacanje(rokovi su prosli, nemate vise pismenih za ispravljat, bla bla) dat cu vam ja jos zadataka za rjesavat, just say the word.
Hmm, vidim ja da vi stvarno nemate pametnijeg posla nego se zafrkajete po ovom topicu. Uz sve te silne i umne rasprave i kako zapravo je konacni integral smisao zivota, mogli bi meni jednostavno rijesit zadatak, a kako ocito imate vrimena na bacanje(rokovi su prosli, nemate vise pismenih za ispravljat, bla bla) dat cu vam ja jos zadataka za rjesavat, just say the word.
_________________
"From this proposition it will follow, when arithmetical addition has been defined, that 1+1=2."
Page 360, Principia Mathematica
|
|
| [Vrh] |
|
Ante
Forumaš(ica)
Pridružen/a: 17. 02. 2006. (11:12:00)
Postovi: (155)16
Spol: 
|
 Postano: 0:19 sri, 1. 3. 2006 Naslov: Postano: 0:19 sri, 1. 3. 2006 Naslov: |
    |
|
|
[quote="zeix"]Hmm, vidim ja da vi stvarno nemate pametnijeg posla nego se zafrkajete po ovom topicu. Uz sve te silne i umne rasprave i kako zapravo je konacni integral smisao zivota, mogli bi meni jednostavno rijesit zadatak, a kako ocito imate vrimena na bacanje(rokovi su prosli, nemate vise pismenih za ispravljat, bla bla) dat cu vam ja jos zadataka za rjesavat, just say the word.[/quote]
I to mi je hvala sta san ti texira ovaj isti zadatak? :P
Konacni integral JEST smisao zivota. Dokaz je trivijalan. :)
[size=7]btw, vsego ce nas upucat sve redom... ja sam za to da mu netko ode iskopcat struju u kabinet...[/size]
[color=darkred][b]EDIT:[/b][/color]
Zaboravih obavezni integral... [latex]\int ^{1}_{0}\frac{1}{1+x^{2}}dx = \sum ^{\infty}_{0}\frac{(-1)^{k}}{2k+1} = \frac{\pi}{4}[/latex]
Cheers!
| zeix (napisa): | | Hmm, vidim ja da vi stvarno nemate pametnijeg posla nego se zafrkajete po ovom topicu. Uz sve te silne i umne rasprave i kako zapravo je konacni integral smisao zivota, mogli bi meni jednostavno rijesit zadatak, a kako ocito imate vrimena na bacanje(rokovi su prosli, nemate vise pismenih za ispravljat, bla bla) dat cu vam ja jos zadataka za rjesavat, just say the word. |
I to mi je hvala sta san ti texira ovaj isti zadatak? 
Konacni integral JEST smisao zivota. Dokaz je trivijalan. 
btw, vsego ce nas upucat sve redom... ja sam za to da mu netko ode iskopcat struju u kabinet...
EDIT:
Zaboravih obavezni integral... 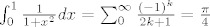
Cheers!
_________________
Eat a lot, sleep a lot, brush 'em like crazy.
Run a lot, do a lot, never be lazy.
Zadnja promjena: Ante; 0:42 sri, 1. 3. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
zeix
Forumaš(ica)

Pridružen/a: 18. 02. 2006. (12:39:11)
Postovi: (75)16
|
 Postano: 0:33 sri, 1. 3. 2006 Naslov: Postano: 0:33 sri, 1. 3. 2006 Naslov: |
    |
|
|
E nemoj se sad pravit da si ti neki dobar guy jer si mi texira zadatak. You are evil. Zna si da ce se exodus pojavit ako stavim ovaj zadatak, a onda si malo prica s njim, i onda si mu zabija noz u ledja. To je sve dio tvog plana. Ajde Exodus, zapitaj se malo, odakle odjednom imas za 1 manju karmu. Ha Ha Ha. Pericius is evil I tell you, evil :evil: :twisted: :twisted:
E nemoj se sad pravit da si ti neki dobar guy jer si mi texira zadatak. You are evil. Zna si da ce se exodus pojavit ako stavim ovaj zadatak, a onda si malo prica s njim, i onda si mu zabija noz u ledja. To je sve dio tvog plana. Ajde Exodus, zapitaj se malo, odakle odjednom imas za 1 manju karmu. Ha Ha Ha. Pericius is evil I tell you, evil   
_________________
"From this proposition it will follow, when arithmetical addition has been defined, that 1+1=2."
Page 360, Principia Mathematica
|
|
| [Vrh] |
|
|














