| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 17:23 pet, 3. 3. 2006 Naslov: Postano: 17:23 pet, 3. 3. 2006 Naslov: |
    |
|
|
malo pojašnjenje mi treba oko uniformne neprekidnosti...
Znači ako je uniformno neprekidna =>neprekidnost, dok sama neprekidnost ne povlači uniformnu neprekidnost.
e sad uniformna ili ti jednoliko neprekidna, pitanje danas na usmenom je bilo kako to vidimo odma da li je ili nije uniformno neprekidna.. e sad ja to ne mogu baš vidjeti odma?? kak se to vidi?? konstantni primjeri su da su uniformno neprekidne fje identiteta i f(x)=x^2 ali na nekom segmentu, tj.f:[a,b]->R, pa se to raspisuje dalje, ali je prof. pitao kak mi sad znamo da je to uniformno neprekidno, tj. [u]zašto smo baš to izabrali[/u]??
malo pojašnjenje mi treba oko uniformne neprekidnosti...
Znači ako je uniformno neprekidna =>neprekidnost, dok sama neprekidnost ne povlači uniformnu neprekidnost.
e sad uniformna ili ti jednoliko neprekidna, pitanje danas na usmenom je bilo kako to vidimo odma da li je ili nije uniformno neprekidna.. e sad ja to ne mogu baš vidjeti odma?? kak se to vidi?? konstantni primjeri su da su uniformno neprekidne fje identiteta i f(x)=x^2 ali na nekom segmentu, tj.f:[a,b]->R, pa se to raspisuje dalje, ali je prof. pitao kak mi sad znamo da je to uniformno neprekidno, tj. zašto smo baš to izabrali??
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 17:46 pet, 3. 3. 2006 Naslov: Postano: 17:46 pet, 3. 3. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]malo pojašnjenje mi treba oko uniformne neprekidnosti...
Znači ako je uniformno neprekidna =>neprekidnost, dok sama neprekidnost ne povlači uniformnu neprekidnost.
e sad uniformna ili ti jednoliko neprekidna, pitanje danas na usmenom je bilo kako to vidimo odma da li je ili nije uniformno neprekidna.. e sad ja to ne mogu baš vidjeti odma?? kak se to vidi?? konstantni primjeri su da su uniformno neprekidne fje identiteta i f(x)=x^2 ali na nekom segmentu, tj.f:[a,b]->R, pa se to raspisuje dalje, ali je prof. pitao kak mi sad znamo da je to uniformno neprekidno, tj. [u]zašto smo baš to izabrali[/u]??[/quote]
pa bilo koja neprekidna funkcija koju promatramo na segmentu je uniformno neprekidna, a inace,ako gledas na cijeloj domeni npr., ne smije imat u nekoj tocki limes + ili - beskonacno, u smislu, ako funkcijske vrijednosti nekontrolirano brzo rastu/padaju, to nije dobro za uniformnu neprekidnost. tak npr. 1/x ocito nije uniformno neprekidna na domeni jer u okolini 0 je malo divlja... ako je gledas na segmentu, onda, naravno, jest uniformno nepr. eto, slikovito i u obliku pricice... :lol:
| Anonymous (napisa): | malo pojašnjenje mi treba oko uniformne neprekidnosti...
Znači ako je uniformno neprekidna =>neprekidnost, dok sama neprekidnost ne povlači uniformnu neprekidnost.
e sad uniformna ili ti jednoliko neprekidna, pitanje danas na usmenom je bilo kako to vidimo odma da li je ili nije uniformno neprekidna.. e sad ja to ne mogu baš vidjeti odma?? kak se to vidi?? konstantni primjeri su da su uniformno neprekidne fje identiteta i f(x)=x^2 ali na nekom segmentu, tj.f:[a,b]->R, pa se to raspisuje dalje, ali je prof. pitao kak mi sad znamo da je to uniformno neprekidno, tj. zašto smo baš to izabrali?? |
pa bilo koja neprekidna funkcija koju promatramo na segmentu je uniformno neprekidna, a inace,ako gledas na cijeloj domeni npr., ne smije imat u nekoj tocki limes + ili - beskonacno, u smislu, ako funkcijske vrijednosti nekontrolirano brzo rastu/padaju, to nije dobro za uniformnu neprekidnost. tak npr. 1/x ocito nije uniformno neprekidna na domeni jer u okolini 0 je malo divlja... ako je gledas na segmentu, onda, naravno, jest uniformno nepr. eto, slikovito i u obliku pricice... 
|
|
| [Vrh] |
|
Gost
|
 Postano: 18:47 pet, 3. 3. 2006 Naslov: Postano: 18:47 pet, 3. 3. 2006 Naslov: |
    |
|
|
hvala, puno jasnije :)
[quote] pa bilo koja neprekidna funkcija koju promatramo na segmentu je uniformno neprekidna[/quote] a ako je interval u pitanju?
i još nešto, kod Lipschitzovog svojstva, isti primjer, dakle f(x)=x^2
f:[a,b]->R, i sad kao gleda se derivacija u desnom kutu fje (zašto?), i onda se upravo za taj lambda uzima derivacija od f u točki b???
bio je pr f(x)=x^2, f:[-2,5]->R i sad u dokazu x,x' iz [-2,5] |f(x)-f(x')|=|x^2-x'^2| i sad se postavljalo pitanje dal je |x+x'|<=10, što je ustvari trivijalno i vrijedi, al me zanima zašto se uzima derivacija u toj rubnoj točki
hvala, puno jasnije 
| Citat: | | pa bilo koja neprekidna funkcija koju promatramo na segmentu je uniformno neprekidna |
a ako je interval u pitanju?
i još nešto, kod Lipschitzovog svojstva, isti primjer, dakle f(x)=x^2
f:[a,b]→R, i sad kao gleda se derivacija u desnom kutu fje (zašto?), i onda se upravo za taj lambda uzima derivacija od f u točki b???
bio je pr f(x)=x^2, f:[-2,5]→R i sad u dokazu x,x' iz [-2,5] |f(x)-f(x')|=|x^2-x'^2| i sad se postavljalo pitanje dal je |x+x'|⇐10, što je ustvari trivijalno i vrijedi, al me zanima zašto se uzima derivacija u toj rubnoj točki
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 22:07 pet, 3. 3. 2006 Naslov: Postano: 22:07 pet, 3. 3. 2006 Naslov: |
    |
|
|
[quote="Anonymus"]a ako je interval u pitanju?[/quote]
neee, nikako ne, pa u tome je i stvar... kad bi vrijedilo i za otvoreni interval, onda bi nepr i unif nepr bili jedno te isto i zasto bi uopce imali oboje...
pogledaj dokaz sa analize 2 da su na segmentu nepr povlaci un. nepr., mislim da ce ti bit puno jasnije... a mozda malo i definiciju un. nepr. :D
[quote="Anonymous"]i još nešto, kod Lipschitzovog svojstva, isti primjer, dakle f(x)=x^2
f:[a,b]->R, i sad kao gleda se derivacija u desnom kutu fje (zašto?), i onda se upravo za taj lambda uzima derivacija od f u točki b???
bio je pr f(x)=x^2, f:[-2,5]->R i sad u dokazu x,x' iz [-2,5] |f(x)-f(x')|=|x^2-x'^2| i sad se postavljalo pitanje dal je |x+x'|<=10, što je ustvari trivijalno i vrijedi, al me zanima zašto se uzima derivacija u toj rubnoj točki[/quote]
ma ne gleda se u desnom kutu opcenito, nego se tu to tak potrefilo... nisam tocno sigurna kaj pitas, slobodno reci ak sam profulala...
znaci, ako nam je funkcija klase C 1 to povlaci lipschitzovost i to bas na nacin da nam je taj lambda određen sa vrijednošću derivacije na tom segmentu prema Lagrangeovom tm srednje vrijednosti(najvecom vrijednoscu).. sad, posto je interval bio slucajno takav da je derivacija imala najvecu vrijednost u desnom rubu, onda smo gledali desni rub... :kravica:
| Anonymus (napisa): | | a ako je interval u pitanju? |
neee, nikako ne, pa u tome je i stvar... kad bi vrijedilo i za otvoreni interval, onda bi nepr i unif nepr bili jedno te isto i zasto bi uopce imali oboje...
pogledaj dokaz sa analize 2 da su na segmentu nepr povlaci un. nepr., mislim da ce ti bit puno jasnije... a mozda malo i definiciju un. nepr. 
| Anonymous (napisa): | i još nešto, kod Lipschitzovog svojstva, isti primjer, dakle f(x)=x^2
f:[a,b]→R, i sad kao gleda se derivacija u desnom kutu fje (zašto?), i onda se upravo za taj lambda uzima derivacija od f u točki b???
bio je pr f(x)=x^2, f:[-2,5]→R i sad u dokazu x,x' iz [-2,5] |f(x)-f(x')|=|x^2-x'^2| i sad se postavljalo pitanje dal je |x+x'|⇐10, što je ustvari trivijalno i vrijedi, al me zanima zašto se uzima derivacija u toj rubnoj točki |
ma ne gleda se u desnom kutu opcenito, nego se tu to tak potrefilo... nisam tocno sigurna kaj pitas, slobodno reci ak sam profulala...
znaci, ako nam je funkcija klase C 1 to povlaci lipschitzovost i to bas na nacin da nam je taj lambda određen sa vrijednošću derivacije na tom segmentu prema Lagrangeovom tm srednje vrijednosti(najvecom vrijednoscu).. sad, posto je interval bio slucajno takav da je derivacija imala najvecu vrijednost u desnom rubu, onda smo gledali desni rub... 
|
|
| [Vrh] |
|
luce
Forumaš(ica)


Pridružen/a: 08. 02. 2006. (19:47:22)
Postovi: (5A)16
Spol: 
|
 Postano: 16:58 sub, 4. 3. 2006 Naslov: Postano: 16:58 sub, 4. 3. 2006 Naslov: |
    |
|
|
[quote="Ignavia"][quote="Anonymus"]a ako je interval u pitanju?[/quote]
neee, nikako ne, pa u tome je i stvar... kad bi vrijedilo i za otvoreni interval, onda bi nepr i unif nepr bili jedno te isto i zasto bi uopce imali oboje...
pogledaj dokaz sa analize 2 da su na segmentu nepr povlaci un. nepr., mislim da ce ti bit puno jasnije... a mozda malo i definiciju un. nepr. :D
[/quote]
ispravak;
da, ako je interval podskup nekog segmenta na kojem je fja unif. nepr. npr x*x na <-1,3>
| Ignavia (napisa): | | Anonymus (napisa): | | a ako je interval u pitanju? |
neee, nikako ne, pa u tome je i stvar... kad bi vrijedilo i za otvoreni interval, onda bi nepr i unif nepr bili jedno te isto i zasto bi uopce imali oboje...
pogledaj dokaz sa analize 2 da su na segmentu nepr povlaci un. nepr., mislim da ce ti bit puno jasnije... a mozda malo i definiciju un. nepr. 
|
ispravak;
da, ako je interval podskup nekog segmenta na kojem je fja unif. nepr. npr x*x na ←1,3>
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 18:30 sub, 4. 3. 2006 Naslov: Postano: 18:30 sub, 4. 3. 2006 Naslov: |
    |
|
|
[quote="luce"][quote="Ignavia"][quote="Anonymus"]a ako je interval u pitanju?[/quote]
neee, nikako ne, pa u tome je i stvar... kad bi vrijedilo i za otvoreni interval, onda bi nepr i unif nepr bili jedno te isto i zasto bi uopce imali oboje...
pogledaj dokaz sa analize 2 da su na segmentu nepr povlaci un. nepr., mislim da ce ti bit puno jasnije... a mozda malo i definiciju un. nepr. :D
[/quote]
ispravak;
da, ako je interval podskup nekog segmenta na kojem je fja unif. nepr. npr x*x na <-1,3>[/quote]
Nije ispravak nego napomena :ccc: :P
Ako je funkcija uniformno neprekidna na nekom skupu, onda je uniformno neprekidna i na svakom podskupu tog skupa sto je jasno iz definicije :D
Ovo sa intervalom i segmentom je primjer takvog slucaja. Opcenito, funkcija koja je neprekidna na intervalu nije uniformno neprekidna
| luce (napisa): | | Ignavia (napisa): | | Anonymus (napisa): | | a ako je interval u pitanju? |
neee, nikako ne, pa u tome je i stvar... kad bi vrijedilo i za otvoreni interval, onda bi nepr i unif nepr bili jedno te isto i zasto bi uopce imali oboje...
pogledaj dokaz sa analize 2 da su na segmentu nepr povlaci un. nepr., mislim da ce ti bit puno jasnije... a mozda malo i definiciju un. nepr. 
|
ispravak;
da, ako je interval podskup nekog segmenta na kojem je fja unif. nepr. npr x*x na ←1,3> |
Nije ispravak nego napomena  
Ako je funkcija uniformno neprekidna na nekom skupu, onda je uniformno neprekidna i na svakom podskupu tog skupa sto je jasno iz definicije 
Ovo sa intervalom i segmentom je primjer takvog slucaja. Opcenito, funkcija koja je neprekidna na intervalu nije uniformno neprekidna
_________________
Bri
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 18:42 sub, 4. 3. 2006 Naslov: Postano: 18:42 sub, 4. 3. 2006 Naslov: |
    |
|
|
Grga, koji si ti kavalir postao... :romeo: :anifaint: :navijacica: :trio:
@luce: al super ti je napomena, stvarno, nisam se sjetila to nadodati, a nisam sigurna da bi gost to sam dokucio... :okgreen:
goste, javi se i opovrgni klevetu :lol:
Grga, koji si ti kavalir postao...    
@luce: al super ti je napomena, stvarno, nisam se sjetila to nadodati, a nisam sigurna da bi gost to sam dokucio... 
goste, javi se i opovrgni klevetu 
|
|
| [Vrh] |
|
Gost
|
 Postano: 16:25 ned, 5. 3. 2006 Naslov: Postano: 16:25 ned, 5. 3. 2006 Naslov: |
    |
|
|
dakle ljudi hvala vam :)
i da,da luce napomena ti je super :miniklap:
tek sam počela tu analizu pa još ne baratam s tim svim, budući da je ma2 bila davno... 8-[
e a ovo sa Lipschitzom...ma taj lambda kad se trebao odrediti se ustvari gledala derivacija fje, u tom primjeru u desnom rubu,zato kaj uzima max, naravno ne općenito, sam si nisam mogla povezati zašto gleda derivaciju
dakle ljudi hvala vam 
i da,da luce napomena ti je super 
tek sam počela tu analizu pa još ne baratam s tim svim, budući da je ma2 bila davno... 
e a ovo sa Lipschitzom...ma taj lambda kad se trebao odrediti se ustvari gledala derivacija fje, u tom primjeru u desnom rubu,zato kaj uzima max, naravno ne općenito, sam si nisam mogla povezati zašto gleda derivaciju
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
 Postano: 20:05 uto, 7. 3. 2006 Naslov: Postano: 20:05 uto, 7. 3. 2006 Naslov: |
    |
|
|
e, jos nije dobro za uniformnu neprekidnost niti kad funkcija previse "titra"; npr. g(x)= sin(2pi/x), za x iz <0,1]; onak slikovito, ova funkcija previse titra u blizini nule, pa zato nije uniformno neprekidna :bird:
e, jos nije dobro za uniformnu neprekidnost niti kad funkcija previse "titra"; npr. g(x)= sin(2pi/x), za x iz <0,1]; onak slikovito, ova funkcija previse titra u blizini nule, pa zato nije uniformno neprekidna 
_________________ Laganini...i stprljivo....  |
|
| [Vrh] |
|
anet
Gost
|
|
| [Vrh] |
|
Meri
Forumaš(ica)

Pridružen/a: 11. 11. 2004. (14:48:32)
Postovi: (155)16
Spol: 
Lokacija: Zagreb, Zaaaaagreb...tararam...
|
 Postano: 22:14 čet, 9. 3. 2006 Naslov: Postano: 22:14 čet, 9. 3. 2006 Naslov: |
    |
|
|
[quote="anet"]e a ako uzmem za primjer linearni operator, kao sa R^n->R^n i ak me traži da mu to dokažem... kak se to raspiše?[/quote]
mi znamo da je svaki lineran operator omeden, pa onda takoder i znamo da ima lipschitzovo svojstvo; a znamo da ako, funkcija opcenito, ima lipshitzovo svosjstvo da je onda uniformno neprekidna.
btw, to su u skripti tm2.20, tm.2.21, korolar 2.22
| anet (napisa): | | e a ako uzmem za primjer linearni operator, kao sa R^n->R^n i ak me traži da mu to dokažem... kak se to raspiše? |
mi znamo da je svaki lineran operator omeden, pa onda takoder i znamo da ima lipschitzovo svojstvo; a znamo da ako, funkcija opcenito, ima lipshitzovo svosjstvo da je onda uniformno neprekidna.
btw, to su u skripti tm2.20, tm.2.21, korolar 2.22
_________________ Laganini...i stprljivo....  |
|
| [Vrh] |
|
dokaz
Gost
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 1:15 pon, 29. 9. 2008 Naslov: Re: dokaz Postano: 1:15 pon, 29. 9. 2008 Naslov: Re: dokaz |
    |
|
|
[quote="dokaz"]kako se moze dokazati da je npr f(x)=x^2 uniformno ne prekidna na segmentu[-a,a].[/quote]
Funkcija [latex]f(x)=x^{2}[/latex] je neprekidna na cijeloj domeni, jer je elementarna, pa je neprekidna i na segmentu [latex][-a,a][/latex]. Taj segment je kompaktan skup (jer je ograničen i zatvoren), pa po teoremu 7.6 iz skripte, f je uniformno neprekidna na tom segmentu.
| dokaz (napisa): | | kako se moze dokazati da je npr f(x)=x^2 uniformno ne prekidna na segmentu[-a,a]. |
Funkcija 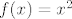 je neprekidna na cijeloj domeni, jer je elementarna, pa je neprekidna i na segmentu je neprekidna na cijeloj domeni, jer je elementarna, pa je neprekidna i na segmentu 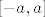 . Taj segment je kompaktan skup (jer je ograničen i zatvoren), pa po teoremu 7.6 iz skripte, f je uniformno neprekidna na tom segmentu. . Taj segment je kompaktan skup (jer je ograničen i zatvoren), pa po teoremu 7.6 iz skripte, f je uniformno neprekidna na tom segmentu.
|
|
| [Vrh] |
|
confused
Gost
|
 Postano: 20:17 sub, 4. 9. 2010 Naslov: Postano: 20:17 sub, 4. 9. 2010 Naslov: |
    |
|
|
Mene pak zanima, konkretno, kod funkcije triju varijabli, da li uvodim kakvu restrikciju prilikom provjeravanja uniformne neprekidnosti (jer pricica sa kvadraticem ne pali)... Npr, konkretno, kako bi se za bezveznu f:R^3->R, f(x,y,z)=2x+3y-z provjerila uniformna neprekidnost po definiciji?
Mene pak zanima, konkretno, kod funkcije triju varijabli, da li uvodim kakvu restrikciju prilikom provjeravanja uniformne neprekidnosti (jer pricica sa kvadraticem ne pali)... Npr, konkretno, kako bi se za bezveznu f:R^3->R, f(x,y,z)=2x+3y-z provjerila uniformna neprekidnost po definiciji?
|
|
| [Vrh] |
|
|












