Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

rekurzivne relacije (objasnjenje gradiva)
WWW:

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Linearna algebra 1 & 2 (za inženjerske smjerove)
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
alen
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
Sarma = la pohva - posuda
132 = 230 - 98
PostPostano: 12:52 sub, 8. 4. 2006    Naslov: rekurzivne relacije Citirajte i odgovorite
smije li se potenciranje matrica primjeniti kada imamo na primjer ovisnost
a_(n+2)=a_(n+1)-n*(n-1)*a_n ?
smije li se potenciranje matrica primjeniti kada imamo na primjer ovisnost
a_(n+2)=a_(n+1)-n*(n-1)*a_n ?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
nenad
Moderator
Moderator


Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
Sarma = la pohva - posuda
92 = 106 - 14
PostPostano: 17:21 sub, 8. 4. 2006    Naslov: Citirajte i odgovorite
[quote]smije li se potenciranje matrica primjeniti kada imamo na primjer ovisnost
a_(n+2)=a_(n+1)-n*(n-1)*a_n ?
[/quote]
Hmm ... Na prvi pogled, pitanje mi nije jasno. Recimo da to ovako shvatim.

Radi se o dvokoračnoj rekurziji, i trik je (kao i za diferencijalne jednadžbe :-)
da se to svede na sustav jednokoračnih (ili prvog reda). Uvedimo:
b_(n+1)=a_n, pa imamo
a_(n+1)=a_n-(n-1)*(n-2)*b_n
b_(n+1)=a_n

Matrica glasi:
[latex]{\bf A}_n=\left[\matrix{1 & -(n-1)(n-2)\cr 1 & 0 \cr}\right][/latex]

Ako znamo a_0=b_1 i a_1, onda možemo računati ...
Jedino što je sada problem u tome što je A_n različita, i veliko je pitanje kako izračunati
produkt A_n A_(n-1)... A_1 .
Ovdje ne vidim odmah pametnog načina.
(za diferencijalne jednadžbe ovo bi odgovaralo promjenjivim koeficijentima; za što
treba koristiti druge metode :-(

Možda u ovom primjeru postoji neki lagani trik, ali ga ja sada ne vidim.

- Nenad Antonić
Citat:
smije li se potenciranje matrica primjeniti kada imamo na primjer ovisnost
a_(n+2)=a_(n+1)-n*(n-1)*a_n ?

Hmm ... Na prvi pogled, pitanje mi nije jasno. Recimo da to ovako shvatim.

Radi se o dvokoračnoj rekurziji, i trik je (kao i za diferencijalne jednadžbe Smile
da se to svede na sustav jednokoračnih (ili prvog reda). Uvedimo:
b_(n+1)=a_n, pa imamo
a_(n+1)=a_n-(n-1)*(n-2)*b_n
b_(n+1)=a_n

Matrica glasi:


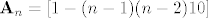
Ako znamo a_0=b_1 i a_1, onda možemo računati ...
Jedino što je sada problem u tome što je A_n različita, i veliko je pitanje kako izračunati
produkt A_n A_(n-1)... A_1 .
Ovdje ne vidim odmah pametnog načina.
(za diferencijalne jednadžbe ovo bi odgovaralo promjenjivim koeficijentima; za što
treba koristiti druge metode Sad

Možda u ovom primjeru postoji neki lagani trik, ali ga ja sada ne vidim.

- Nenad Antonić


[Vrh]
Korisnički profil Pošaljite privatnu poruku
alen
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
Sarma = la pohva - posuda
132 = 230 - 98
PostPostano: 20:24 sub, 8. 4. 2006    Naslov: Citirajte i odgovorite
da, pitao sam to zato sto su svi primjeri koje smo radili na vjezbama bili sa fiksnim koeficijentima u rekurzivnoj relaciji, a ovi su promjenjivi, kako vi kazete. znaci, tu ne mogu primjeniti matricno potenciranje :( . steta. hvala na odgovoru
da, pitao sam to zato sto su svi primjeri koje smo radili na vjezbama bili sa fiksnim koeficijentima u rekurzivnoj relaciji, a ovi su promjenjivi, kako vi kazete. znaci, tu ne mogu primjeniti matricno potenciranje Sad . steta. hvala na odgovoru


[Vrh]
Korisnički profil Pošaljite privatnu poruku
alen
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
Sarma = la pohva - posuda
132 = 230 - 98
PostPostano: 11:46 ned, 9. 4. 2006    Naslov: Citirajte i odgovorite
nego, evo vec sam lagano ocajan, zanima me da li bi se te metode iz diferencijalnih jednadzbi mogle ovdje primjeniti?
(valjda nisu previse komplicirane)
nego, evo vec sam lagano ocajan, zanima me da li bi se te metode iz diferencijalnih jednadzbi mogle ovdje primjeniti?
(valjda nisu previse komplicirane)


[Vrh]
Korisnički profil Pošaljite privatnu poruku
nana
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: žensko
Sarma = la pohva - posuda
95 = 158 - 63
PostPostano: 12:58 ned, 9. 4. 2006    Naslov: Citirajte i odgovorite
Ako znamo da je n=100 tj. 101 mozemo li onda ovom metodom ? :grebgreb:
Ako znamo da je n=100 tj. 101 mozemo li onda ovom metodom ? Kotacici rade 100 na sat



_________________
Kad sam bila mala htjela sam biti statističarka Very Happy
[tex]\omega \in \Omega[/tex] Srce
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
alen
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
Sarma = la pohva - posuda
132 = 230 - 98
PostPostano: 13:04 ned, 9. 4. 2006    Naslov: Citirajte i odgovorite
nana zeli reci da ovo nema nikakve veze sa nasom zadacom iz matematicke analize nego nas jako zanima kada smijemo primjeniti matricno potenciranje :lol:

salim se, ali stvarno nas zanima da li to mozemo primjeniti ako znamo koliki nam je n (nekako slutim da ce odgovor biti negativan)
nana zeli reci da ovo nema nikakve veze sa nasom zadacom iz matematicke analize nego nas jako zanima kada smijemo primjeniti matricno potenciranje Laughing

salim se, ali stvarno nas zanima da li to mozemo primjeniti ako znamo koliki nam je n (nekako slutim da ce odgovor biti negativan)


[Vrh]
Korisnički profil Pošaljite privatnu poruku
nenad
Moderator
Moderator


Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
Sarma = la pohva - posuda
92 = 106 - 14
PostPostano: 13:05 ned, 9. 4. 2006    Naslov: Citirajte i odgovorite
Možda ovo pomogne. Postoji pravilnost.
Treba je uočiti, i dokazati.

Naravno, uz pretpostavku da ja nisam nešto krivo upisao :-)

- Nenad
Možda ovo pomogne. Postoji pravilnost.
Treba je uočiti, i dokazati.

Naravno, uz pretpostavku da ja nisam nešto krivo upisao Smile

- Nenad




alen.pdf
 Description:
Maple račun

Download
 Filename:  alen.pdf
 Filesize:  110.88 KB
 Downloaded:  243 Time(s)
[Vrh]
Korisnički profil Pošaljite privatnu poruku
alen
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
Sarma = la pohva - posuda
132 = 230 - 98
PostPostano: 13:08 ned, 9. 4. 2006    Naslov: Citirajte i odgovorite
hvala profesore. izgleda da ce se i nana sa mnom sada baciti na posao
hvala profesore. izgleda da ce se i nana sa mnom sada baciti na posao


[Vrh]
Korisnički profil Pošaljite privatnu poruku
nenad
Moderator
Moderator


Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
Sarma = la pohva - posuda
92 = 106 - 14
PostPostano: 13:13 ned, 9. 4. 2006    Naslov: Citirajte i odgovorite
Za n=100 (to je moj n!) dobije se:[code:1]
B := matrix([[-277686642445533804805955647133001296149392658742473494042061276603389784048886391652075187088298742783664427150091895088287743720918910421788692474365234375, 0], [11045957254454140658328020898054709257804734206110016727893051735435362167563424844112337791428930842827940409513912075034252024220775333650112152099609375, 0]])[/code:1]

Ne zam pomaže li kome :?:

- Nenad
Za n=100 (to je moj n!) dobije se:
Kod:

B := matrix([[-277686642445533804805955647133001296149392658742473494042061276603389784048886391652075187088298742783664427150091895088287743720918910421788692474365234375, 0], [11045957254454140658328020898054709257804734206110016727893051735435362167563424844112337791428930842827940409513912075034252024220775333650112152099609375, 0]])


Ne zam pomaže li kome Question

- Nenad


[Vrh]
Korisnički profil Pošaljite privatnu poruku
alen
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
Sarma = la pohva - posuda
132 = 230 - 98
PostPostano: 13:22 ned, 9. 4. 2006    Naslov: Citirajte i odgovorite
jupi. znao sam da mora ispast neko lijepo rijesenje. ovo je sam vrh elegancije. sto nam to na analizi daju da rijesavamo :cry:

joj da, profesore, hvala na trudu, pomaze da provjerimo poslije da li je rijesenje tocno
jupi. znao sam da mora ispast neko lijepo rijesenje. ovo je sam vrh elegancije. sto nam to na analizi daju da rijesavamo Crying or Very sad

joj da, profesore, hvala na trudu, pomaze da provjerimo poslije da li je rijesenje tocno


[Vrh]
Korisnički profil Pošaljite privatnu poruku
alen
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
Sarma = la pohva - posuda
132 = 230 - 98
PostPostano: 22:08 ned, 9. 4. 2006    Naslov: Citirajte i odgovorite
izlgeda da se ipak ne mora odrediti 100. i 101. clan, nego samo 5. i 6.

nazalost, nisam uspio uociti pravilnost medu onim matricama, ali dobro, to ostavljam za vise godine :)

hvala jos jednom
izlgeda da se ipak ne mora odrediti 100. i 101. clan, nego samo 5. i 6.

nazalost, nisam uspio uociti pravilnost medu onim matricama, ali dobro, to ostavljam za vise godine Smile

hvala jos jednom


[Vrh]
Korisnički profil Pošaljite privatnu poruku
nenad
Moderator
Moderator


Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
Sarma = la pohva - posuda
92 = 106 - 14
PostPostano: 22:55 ned, 9. 4. 2006    Naslov: Citirajte i odgovorite
[quote]izlgeda da se ipak ne mora odrediti 100. i 101. clan, nego samo 5. i 6. [/quote]
Onda je u onom PDF prilogu rješenje.

- Nenad
Citat:
izlgeda da se ipak ne mora odrediti 100. i 101. clan, nego samo 5. i 6.

Onda je u onom PDF prilogu rješenje.

- Nenad


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Linearna algebra 1 & 2 (za inženjerske smjerove) Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan