|
[quote="Wuvie"]Znam da gnjavim, ali nešto me uvijek zanimalo. Zašto recimo kad definiramo funkciju f sa skupa X na skup Y kažemo da je to uređena trojka (X,Y,f)? Ili kad definiramo grupu kažemo uređeni par (G,+). Jel to isti uređeni par kao (a,b)? Jel se to isto može zapisati kao skup
{{a},{a,b}}? Mislim jel taj zapis nečem služi ili je to samo kao oznaka? :?[/quote]
Teoretski gledano služi. :D Davno sam polagao teoriju skupova pa se nadam da neću nešto krivo reći (u slučaju da tako bude, neka me netko ispravi):
Jedna od standardnih teorija skupova je tzv. Zermelo-Frankelova teorija (ili kraće ZF-teorija). To je jedna teorija prvog reda (što god to sad značilo) i njen osnovni term je skup, te dva skupa su po definiciji jednaka akko imaju iste elemente (tzv. [i]aksiom ekstenzionalnosti[/i]).
Znači svaki objekt kojeg "izgradimo" u toj teoriji je skup, kao npr. funkcija, grupa, itd. Npr. [i]kartezijev produkt[/i] [latex]X \times Y[/latex] skupova [latex]X[/latex] i [latex]Y[/latex] definiramo kao skup svih terma "oblika" [latex](x,y):=\{\{x\}, \{x,y\}\}[/latex] pri čemu je [latex]x \in X, \ y \in Y[/latex]. To je dobro definiran pojam (tj. kartezijev produkt skupova je skup) i njegove elemente zovemo [i]uređeni parovi[/i]. Uređeni par smo definirali baš tako iz dva razloga:
1. da bude term te teorije (tj. skup)
2. vrijedi osnovno svojstvo koje bismo htjeli za uređene parove: lako se provjeri da su dva uređena para [latex](x,y)[/latex] i [latex](x',y')[/latex] jednaka (kao skupovi) akko im se "podudaraju koordinate", tj. ako je [latex]x=x'[/latex] i [latex]y=y'[/latex].
Analogno se definiraju uređene trojke, odnosno n-torke i za njih vrijedi isto svojstvo: dvije n-torke su jednake akko im se "podudaraju sve koordinate".
E sad, kada definiramo pojam funkcije u toj teoriji, ona mora biti skup i htjeli bismo da ima osnovno svojstvo: dvije funkcije su jednake akko su im domena, kodomena i "način djelovanja" jednaki. Tu sad možemo pristupiti na više (ekvivalentnih) načina: prvi je možda ovaj koji si ti napisao:[i] funkcija[/i] [latex]f: X \rightarrow Y[/latex] je uređena trojka [latex](X,Y,f)[/latex] (to je sad dobro definiran pojam, tj. skup) pri čemu su [latex]X[/latex] i [latex]Y[/latex] skupovi a [latex]f[/latex] je podskup kartezijevog produkta [latex]X \times Y[/latex] (relacija) sa svojstvom da je domena te relacije (skup svih [latex]x \in X[/latex] za koje postoji [latex]y \in Y[/latex] td. je [latex](x,y) \in f[/latex]) čitav [latex]X[/latex] i da je [latex]f[/latex] [i]funkcionalna[/i], tj. da za svako [latex]x \in X[/latex] postoji jedinstven [latex]y \in Y [/latex] td. je [latex](x,y) \in f[/latex].
Sad je taj izgrađeni objekt kojeg zovemo funkcija dobro definiran pojam (skup) i ima upravo ova svojstva koja želimo: dvije funkcije [latex]f: X \rightarrow Y[/latex] i [latex]g: Z \rightarrow W[/latex] su jednake (kao skupovi) ako su im sve komponente jednake, dakle [latex]X=Z[/latex] i [latex]Y=W[/latex] i "način djelovanja" im je isti (tj. funkcijske relacije im se podudaraju [latex]f=g[/latex]).
Postoji i kraći način definiranja funkcije, samo kao funkcionalne relacije [latex]f \subseteq X \times Y[/latex] čija je domena skup [latex]X[/latex], no ovim gornjim načinom se samo naglašava što znači jednakost dviju funkcija, kao jednakost uređenih trojki.
Analogno u slučaju grupa, nju definiramo kao uređeni par [latex](G, \cdot)[/latex], pri čemu je [latex]G[/latex] skup i [latex]\cdot : G \times G \rightarrow G[/latex] funkcija (binarna operacija) koja zadovoljava neke dodatne aksiome. To opet za jednostavnu posljedicu ima da su dvije grupe [latex](G, \cdot)[/latex] i [latex](H, \circ)[/latex] jednake ako im je ležeći skup isti, tj. [latex]G=H[/latex] i ako je [latex]\cdot=\circ[/latex] (tj. i ako su binarne operacije jednake-kao funkcije).
I zamisli sad da to nisi tako definirao, pa da ti onda (ko fol) ispadne da su dvije grupe jednake ako je prvi skup jednak drugoj binarnoj operaciji i obrnuto, ma tragedija buraz. :cry:
Nadam se da nisam previše zabrazdio i da sam pomogao. :? :D
[size=6]p.s. i nadam se da sam uspio bar malo ispast pametan, ili barem štreberčina. A e...[/size]
| Wuvie (napisa): | Znam da gnjavim, ali nešto me uvijek zanimalo. Zašto recimo kad definiramo funkciju f sa skupa X na skup Y kažemo da je to uređena trojka (X,Y,f)? Ili kad definiramo grupu kažemo uređeni par (G,+). Jel to isti uređeni par kao (a,b)? Jel se to isto može zapisati kao skup
{{a},{a,b}}? Mislim jel taj zapis nečem služi ili je to samo kao oznaka?  |
Teoretski gledano služi.  Davno sam polagao teoriju skupova pa se nadam da neću nešto krivo reći (u slučaju da tako bude, neka me netko ispravi): Davno sam polagao teoriju skupova pa se nadam da neću nešto krivo reći (u slučaju da tako bude, neka me netko ispravi):
Jedna od standardnih teorija skupova je tzv. Zermelo-Frankelova teorija (ili kraće ZF-teorija). To je jedna teorija prvog reda (što god to sad značilo) i njen osnovni term je skup, te dva skupa su po definiciji jednaka akko imaju iste elemente (tzv. aksiom ekstenzionalnosti).
Znači svaki objekt kojeg "izgradimo" u toj teoriji je skup, kao npr. funkcija, grupa, itd. Npr. kartezijev produkt 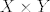 skupova skupova  i i 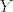 definiramo kao skup svih terma "oblika" definiramo kao skup svih terma "oblika" 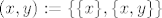 pri čemu je pri čemu je 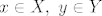 . To je dobro definiran pojam (tj. kartezijev produkt skupova je skup) i njegove elemente zovemo uređeni parovi. Uređeni par smo definirali baš tako iz dva razloga: . To je dobro definiran pojam (tj. kartezijev produkt skupova je skup) i njegove elemente zovemo uređeni parovi. Uređeni par smo definirali baš tako iz dva razloga:
1. da bude term te teorije (tj. skup)
2. vrijedi osnovno svojstvo koje bismo htjeli za uređene parove: lako se provjeri da su dva uređena para 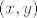 i i 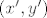 jednaka (kao skupovi) akko im se "podudaraju koordinate", tj. ako je jednaka (kao skupovi) akko im se "podudaraju koordinate", tj. ako je 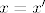 i i 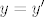 . .
Analogno se definiraju uređene trojke, odnosno n-torke i za njih vrijedi isto svojstvo: dvije n-torke su jednake akko im se "podudaraju sve koordinate".
E sad, kada definiramo pojam funkcije u toj teoriji, ona mora biti skup i htjeli bismo da ima osnovno svojstvo: dvije funkcije su jednake akko su im domena, kodomena i "način djelovanja" jednaki. Tu sad možemo pristupiti na više (ekvivalentnih) načina: prvi je možda ovaj koji si ti napisao: funkcija 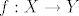 je uređena trojka je uređena trojka 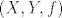 (to je sad dobro definiran pojam, tj. skup) pri čemu su (to je sad dobro definiran pojam, tj. skup) pri čemu su  i i 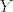 skupovi a skupovi a  je podskup kartezijevog produkta je podskup kartezijevog produkta 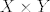 (relacija) sa svojstvom da je domena te relacije (skup svih (relacija) sa svojstvom da je domena te relacije (skup svih  za koje postoji za koje postoji 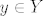 td. je td. je 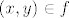 ) čitav ) čitav  i da je i da je  funkcionalna, tj. da za svako funkcionalna, tj. da za svako  postoji jedinstven postoji jedinstven 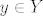 td. je td. je 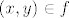 . .
Sad je taj izgrađeni objekt kojeg zovemo funkcija dobro definiran pojam (skup) i ima upravo ova svojstva koja želimo: dvije funkcije 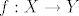 i i  su jednake (kao skupovi) ako su im sve komponente jednake, dakle su jednake (kao skupovi) ako su im sve komponente jednake, dakle 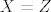 i i 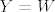 i "način djelovanja" im je isti (tj. funkcijske relacije im se podudaraju i "način djelovanja" im je isti (tj. funkcijske relacije im se podudaraju 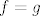 ). ).
Postoji i kraći način definiranja funkcije, samo kao funkcionalne relacije 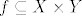 čija je domena skup čija je domena skup  , no ovim gornjim načinom se samo naglašava što znači jednakost dviju funkcija, kao jednakost uređenih trojki. , no ovim gornjim načinom se samo naglašava što znači jednakost dviju funkcija, kao jednakost uređenih trojki.
Analogno u slučaju grupa, nju definiramo kao uređeni par 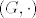 , pri čemu je , pri čemu je 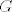 skup i skup i 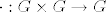 funkcija (binarna operacija) koja zadovoljava neke dodatne aksiome. To opet za jednostavnu posljedicu ima da su dvije grupe funkcija (binarna operacija) koja zadovoljava neke dodatne aksiome. To opet za jednostavnu posljedicu ima da su dvije grupe 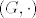 i i 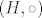 jednake ako im je ležeći skup isti, tj. jednake ako im je ležeći skup isti, tj. 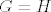 i ako je i ako je 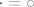 (tj. i ako su binarne operacije jednake-kao funkcije). (tj. i ako su binarne operacije jednake-kao funkcije).
I zamisli sad da to nisi tako definirao, pa da ti onda (ko fol) ispadne da su dvije grupe jednake ako je prvi skup jednak drugoj binarnoj operaciji i obrnuto, ma tragedija buraz. 
Nadam se da nisam previše zabrazdio i da sam pomogao.  
p.s. i nadam se da sam uspio bar malo ispast pametan, ili barem štreberčina. A e...
|




