| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 3:44 sub, 31. 12. 2005 Naslov: Projekcija vektora na konus Postano: 3:44 sub, 31. 12. 2005 Naslov: Projekcija vektora na konus |
    |
|
|
Neki se bune da ovdje ima premalo nastavnih stvari, pa evo jedno pitanje koje me muci vec neko vrijeme:
Neka su dani [latex]F^i \in \{0,1\}^n, i=1,\dots,m[/latex], te neka je [latex]C = \{\sum_{i=1}^m \lambda_i F^i: \lambda_i \geq 0 \}[/latex] konacno generirani konus odredjen tim vektorima. Nadalje, neka je zadan vektor [latex]F \in \mathbb{R}^n_+[/latex].
Trazi se vektor [latex]F' \in C[/latex] takav da je [latex]\|F - F'\| \leq \|F - Y\|\ \forall Y \in C[/latex] (obicna, euklidska norma).
Prihvacam razmisljanja, ideje, upute,... ali bez linkova (osim ako vode na clanke s gotovim rjesenjem). 8)
P.S. Algoritam treba biti efikasan (i) u ovisnosti o dimenziji prostora [i]n[/i]; imam algoritam koji je dobar ako se dimenzija fixira (konkretno na 3), no to mi nije dovoljno dobro. :(
Neki se bune da ovdje ima premalo nastavnih stvari, pa evo jedno pitanje koje me muci vec neko vrijeme:
Neka su dani 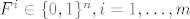 , te neka je , te neka je 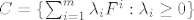 konacno generirani konus odredjen tim vektorima. Nadalje, neka je zadan vektor konacno generirani konus odredjen tim vektorima. Nadalje, neka je zadan vektor 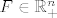 . .
Trazi se vektor 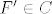 takav da je takav da je 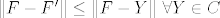 (obicna, euklidska norma). (obicna, euklidska norma).
Prihvacam razmisljanja, ideje, upute,... ali bez linkova (osim ako vode na clanke s gotovim rjesenjem). 
P.S. Algoritam treba biti efikasan (i) u ovisnosti o dimenziji prostora n; imam algoritam koji je dobar ako se dimenzija fixira (konkretno na 3), no to mi nije dovoljno dobro. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
markov
Forumaš(ica)

Pridružen/a: 04. 01. 2006. (01:24:33)
Postovi: (121)16
|
 Postano: 9:44 sri, 4. 1. 2006 Naslov: Možda pomogne Postano: 9:44 sri, 4. 1. 2006 Naslov: Možda pomogne |
    |
|
|
Imam neke ideje, ali do pravog algoritma ima još posla. Uzet ću da su [latex]F^i[/latex] linearno nezavisni.
Projekcija se naravno nalazi na rubu konusa C. Točke iz konusa karakteriziirana je s [latex]\lambda\in[0,\infty)^m[/latex] (zbog linearne neovisnosti), pa točke s ruba imaju u nekim komponentama od [latex]\lambda[/latex] za vrijednost nulu.
Funkcija koju minimiziramo je [latex]g(\lambda)=\|\sum_{i=1}^m \lambda_i F^î-F\|^2[/latex], a gradijent joj je [latex]\nabla g(\lambda)=A^\tau A\lambda - A^\tau F[/latex], gdje matrica [latex]A[/latex] za stupce ima vektore [latex]F^i[/latex].
Imamo jednostavan kriterij za provjeru optimalnosti točke [latex]\lambda^\ast\geq 0[/latex] (slijedi iz zapisa normalnog konusa na C u [latex]\lambda^\ast[/latex]): u [latex]\lambda^\ast[/latex] funkcija g poprima minimum ako i samo ako vrijedi:
Za svaki [latex]i=1\ldots m\quad (\lambda^\ast_i=0 \Leftrightarrow\nabla g(\lambda^\ast)>0)\;\&\;(\lambda^\ast_i>0 \Leftrightarrow\nabla g(\lambda^\ast)=0)[/latex].
Za nastavak bi od velike koristi značila informacija o veličini m. Ako nije velik mogli bi se redom provjeriti dijelovi ruba konusa C. Uzmimo npr dio ruba na kojem je [latex]\lambda_i=0[/latex] za indekse i iz skupa J. S [latex]\tilde\lambda[/latex] označit ćemo vektor sačinjen od ostalih (nenul) komponenti vektora [latex]\lambda[/latex]. Dovoljno je projicirati F na potprostor [latex]\sum_{i\notin J}\lambda_i F^i[/latex]. Po metodi najmanjih kvadrata projekciju (tj. njene nenul komponente) [latex]\tilde\lambda[/latex] nađemo kao rješenje sustava [latex]\tilde A^\tau \tilde A\tilde\lambda =\tilde A^\tau F[/latex], pri čemu matricu [latex]\tilde A[/latex] čine vektori [latex]F^i[/latex] za indekse [latex]i\notin J[/latex] (kao stupci). Ako je neki od [latex]\tilde\lambda_i[/latex] negativan odmah zaključujemo da se na tom dijelu ruba ne poprima minimum. Inače (ako su sve komponente nenegativne) treba provjeriti gornji kriterij optimalnosti.
Ako je m velik, trebalo bi redom (nekim pametnim kriterijem) jednu po jednu komponentu vektora [latex]\lambda[/latex] staviti na nulu - mogla bi pomoći projekcija vektora F na potprostor razapet preostalim vektorima [latex]F^i[/latex] i gradijent funkcije g. Zasad nije nigdje korišten i poseban oblik vektora [latex]F^i[/latex]. Moram ići. Nadam se će pomoći.
Pozdrav
Marko Vrdoljak
Imam neke ideje, ali do pravog algoritma ima još posla. Uzet ću da su 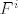 linearno nezavisni. linearno nezavisni.
Projekcija se naravno nalazi na rubu konusa C. Točke iz konusa karakteriziirana je s 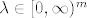 (zbog linearne neovisnosti), pa točke s ruba imaju u nekim komponentama od (zbog linearne neovisnosti), pa točke s ruba imaju u nekim komponentama od  za vrijednost nulu. za vrijednost nulu.
Funkcija koju minimiziramo je 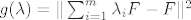 , a gradijent joj je , a gradijent joj je 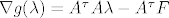 , gdje matrica , gdje matrica  za stupce ima vektore za stupce ima vektore 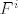 . .
Imamo jednostavan kriterij za provjeru optimalnosti točke  (slijedi iz zapisa normalnog konusa na C u (slijedi iz zapisa normalnog konusa na C u 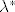 ): u ): u 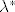 funkcija g poprima minimum ako i samo ako vrijedi: funkcija g poprima minimum ako i samo ako vrijedi:
Za svaki 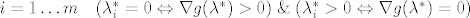 . .
Za nastavak bi od velike koristi značila informacija o veličini m. Ako nije velik mogli bi se redom provjeriti dijelovi ruba konusa C. Uzmimo npr dio ruba na kojem je 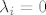 za indekse i iz skupa J. S za indekse i iz skupa J. S 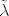 označit ćemo vektor sačinjen od ostalih (nenul) komponenti vektora označit ćemo vektor sačinjen od ostalih (nenul) komponenti vektora  . Dovoljno je projicirati F na potprostor . Dovoljno je projicirati F na potprostor 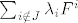 . Po metodi najmanjih kvadrata projekciju (tj. njene nenul komponente) . Po metodi najmanjih kvadrata projekciju (tj. njene nenul komponente) 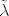 nađemo kao rješenje sustava nađemo kao rješenje sustava 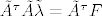 , pri čemu matricu , pri čemu matricu 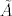 čine vektori čine vektori 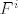 za indekse za indekse 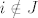 (kao stupci). Ako je neki od (kao stupci). Ako je neki od 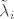 negativan odmah zaključujemo da se na tom dijelu ruba ne poprima minimum. Inače (ako su sve komponente nenegativne) treba provjeriti gornji kriterij optimalnosti. negativan odmah zaključujemo da se na tom dijelu ruba ne poprima minimum. Inače (ako su sve komponente nenegativne) treba provjeriti gornji kriterij optimalnosti.
Ako je m velik, trebalo bi redom (nekim pametnim kriterijem) jednu po jednu komponentu vektora  staviti na nulu - mogla bi pomoći projekcija vektora F na potprostor razapet preostalim vektorima staviti na nulu - mogla bi pomoći projekcija vektora F na potprostor razapet preostalim vektorima 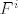 i gradijent funkcije g. Zasad nije nigdje korišten i poseban oblik vektora i gradijent funkcije g. Zasad nije nigdje korišten i poseban oblik vektora 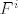 . Moram ići. Nadam se će pomoći. . Moram ići. Nadam se će pomoći.
Pozdrav
Marko Vrdoljak
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 10:43 sri, 4. 1. 2006 Naslov: Re: Možda pomogne Postano: 10:43 sri, 4. 1. 2006 Naslov: Re: Možda pomogne |
    |
|
|
Hvala! :D Potrazit cu te na faxu, a ovdje reply ako netko slucajno prati:
[quote="markov"]Uzet ću da su [latex]F^i[/latex] linearno nezavisni.[/quote]
Svi su na rubu, ali opcenito nisu nezavisni. :( Dapace, imam primjer gdje ih moze biti [latex]O(n^{\sqrt{n}/2})[/latex]. :o
[quote="markov"]Ako je m velik,...[/quote]
Opcenito, [i]m[/i] moze biti jako velik. :? Dimenzija prostora [i]n[/i] je jednaka broju usporedbi koje je netko napravio (problem je potekao iz Teorije odlucivanja). :| Upregne li se cijela stvar u neku automatiku povezanu s mjernim instrumentima, zaobilazimo "zamor" covjeka koji bi radio usporedbe, pa [i]n[/i] moze biti i jako velik. :( A broj generatora je u pravilu veci od dimenzije prostora (ponekad i stravicno veci, kao sto navedoh maloprije). :?
[quote="markov"]...trebalo bi redom (nekim pametnim kriterijem) jednu po jednu komponentu vektora [latex]\lambda[/latex] staviti na nulu - mogla bi pomoći projekcija vektora F na potprostor razapet preostalim vektorima [latex]F^i[/latex] i gradijent funkcije g. Zasad nije nigdje korišten i poseban oblik vektora [latex]F^i[/latex]. Moram ići. Nadam se će pomoći.[/quote]
Eh, tu nastaju problemi. :? [b]Mislim[/b] da se ovo moze napraviti, ali samo zato jer je sve u pozitivnom ortantu (bez tog uvjeta imam protuprimjer), a ja nemam blage kako iskoristiti taj detalj. :(
Naravno, ostaje i cinjenica da generatori konusa nisu nezavisni, no mislim da se to relativno jednostavno zaobidje. :) imam nekakvi iterativni algoritmic koji obavlja taj dio posla, jednom kad znamo kako se (efikasno) dobije projekcija... 8)
Hvala!  Potrazit cu te na faxu, a ovdje reply ako netko slucajno prati: Potrazit cu te na faxu, a ovdje reply ako netko slucajno prati:
| markov (napisa): | Uzet ću da su 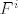 linearno nezavisni. linearno nezavisni. |
Svi su na rubu, ali opcenito nisu nezavisni.  Dapace, imam primjer gdje ih moze biti Dapace, imam primjer gdje ih moze biti 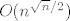 . . 
| markov (napisa): | | Ako je m velik,... |
Opcenito, m moze biti jako velik.  Dimenzija prostora n je jednaka broju usporedbi koje je netko napravio (problem je potekao iz Teorije odlucivanja). Dimenzija prostora n je jednaka broju usporedbi koje je netko napravio (problem je potekao iz Teorije odlucivanja).  Upregne li se cijela stvar u neku automatiku povezanu s mjernim instrumentima, zaobilazimo "zamor" covjeka koji bi radio usporedbe, pa n moze biti i jako velik. Upregne li se cijela stvar u neku automatiku povezanu s mjernim instrumentima, zaobilazimo "zamor" covjeka koji bi radio usporedbe, pa n moze biti i jako velik.  A broj generatora je u pravilu veci od dimenzije prostora (ponekad i stravicno veci, kao sto navedoh maloprije). A broj generatora je u pravilu veci od dimenzije prostora (ponekad i stravicno veci, kao sto navedoh maloprije). 
| markov (napisa): | ...trebalo bi redom (nekim pametnim kriterijem) jednu po jednu komponentu vektora  staviti na nulu - mogla bi pomoći projekcija vektora F na potprostor razapet preostalim vektorima staviti na nulu - mogla bi pomoći projekcija vektora F na potprostor razapet preostalim vektorima 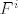 i gradijent funkcije g. Zasad nije nigdje korišten i poseban oblik vektora i gradijent funkcije g. Zasad nije nigdje korišten i poseban oblik vektora 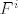 . Moram ići. Nadam se će pomoći. . Moram ići. Nadam se će pomoći. |
Eh, tu nastaju problemi.  Mislim da se ovo moze napraviti, ali samo zato jer je sve u pozitivnom ortantu (bez tog uvjeta imam protuprimjer), a ja nemam blage kako iskoristiti taj detalj. Mislim da se ovo moze napraviti, ali samo zato jer je sve u pozitivnom ortantu (bez tog uvjeta imam protuprimjer), a ja nemam blage kako iskoristiti taj detalj. 
Naravno, ostaje i cinjenica da generatori konusa nisu nezavisni, no mislim da se to relativno jednostavno zaobidje.  imam nekakvi iterativni algoritmic koji obavlja taj dio posla, jednom kad znamo kako se (efikasno) dobije projekcija... imam nekakvi iterativni algoritmic koji obavlja taj dio posla, jednom kad znamo kako se (efikasno) dobije projekcija... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
markov
Forumaš(ica)

Pridružen/a: 04. 01. 2006. (01:24:33)
Postovi: (121)16
|
|
| [Vrh] |
|
|






