| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
apezic
Forumaš(ica)


Pridružen/a: 18. 10. 2005. (15:43:48)
Postovi: (19)16
Spol: 
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 14:59 sub, 11. 2. 2006 Naslov: Re: Catalanovi brojevi? Postano: 14:59 sub, 11. 2. 2006 Naslov: Re: Catalanovi brojevi? |
    |
|
|
[quote="apezic"]Moze li mi itko pomoci i reci kako se pomocu simbolicke metode dobije FI za Catalanove brojeve?[/quote]
Ovako nekako bi islo - nti Catalanov broj je broj najkracih puteva u cjelobrojnoj mrezi od (0, 0) do (n + 1, n + 1) bez diranja dijagonale.
Takav put moze biti ili [i]prazan[/i] (pritom mislim na to da si vec u tocki u koju zelis doci) ili se moze opisati kao put od tocke (1, 0) do neke tocke (k + 1, k te put od tocke (k, k) do tocke (n+1, n+1), s time da oba puta zadovoljavaju prijasnji uvjet.
Sad to pises ovako:
[latex]C = \epsilon + C \times \{ \bullet \} \times C[/latex]
C bi trebalo biti lijepo pisano i predstavlja klasu kombinatornih objekata - puteva od tocke (0, 0) do tocaka oblika (k, k). C prelazi u FI C, epsilon u 1, "tockica" u x, pa dobijes:
[latex]C(x) = 1 + x C(x)^2[/latex]
| apezic (napisa): | | Moze li mi itko pomoci i reci kako se pomocu simbolicke metode dobije FI za Catalanove brojeve? |
Ovako nekako bi islo - nti Catalanov broj je broj najkracih puteva u cjelobrojnoj mrezi od (0, 0) do (n + 1, n + 1) bez diranja dijagonale.
Takav put moze biti ili prazan (pritom mislim na to da si vec u tocki u koju zelis doci) ili se moze opisati kao put od tocke (1, 0) do neke tocke (k + 1, k te put od tocke (k, k) do tocke (n+1, n+1), s time da oba puta zadovoljavaju prijasnji uvjet.
Sad to pises ovako:
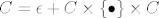
C bi trebalo biti lijepo pisano i predstavlja klasu kombinatornih objekata - puteva od tocke (0, 0) do tocaka oblika (k, k). C prelazi u FI C, epsilon u 1, "tockica" u x, pa dobijes:
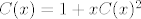
_________________
Bri
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 22:15 uto, 14. 2. 2006 Naslov: Re: Catalanovi brojevi? Postano: 22:15 uto, 14. 2. 2006 Naslov: Re: Catalanovi brojevi? |
    |
|
|
[quote="Grga"][quote="apezic"]Moze li mi itko pomoci i reci kako se pomocu simbolicke metode dobije FI za Catalanove brojeve?[/quote]
Ovako nekako bi islo - nti Catalanov broj je broj najkracih puteva u cjelobrojnoj mrezi od (0, 0) do (n + 1, n + 1) bez diranja dijagonale.
Takav put moze biti ili [i]prazan[/i] (pritom mislim na to da si vec u tocki u koju zelis doci) ili se moze opisati kao put od tocke (1, 0) do neke tocke (k + 1, k te put od tocke (k, k) do tocke (n+1, n+1), s time da oba puta zadovoljavaju prijasnji uvjet.
Sad to pises ovako:
[latex]C = \epsilon + C \times \{ \bullet \} \times C[/latex]
C bi trebalo biti lijepo pisano i predstavlja klasu kombinatornih objekata - puteva od tocke (0, 0) do tocaka oblika (k, k). C prelazi u FI C, epsilon u 1, "tockica" u x, pa dobijes:
[latex]C(x) = 1 + x C(x)^2[/latex][/quote]
posve ista stvar je, a mozda malo ljepsa i razumljivija za gledat, rekurzija za binarna stabla sa n vrhova...
pokazali smo da su to iste rekurzije, pa onda razmizljas ovako: binarno stablo je ili prazno ili se sastoji od korijena i dva podstabla, koja su i sama binarna stabla :shock:
zapis je naravno isti... pa necu ponavljat. sad reci da je ovo bolje :lol:
| Grga (napisa): | | apezic (napisa): | | Moze li mi itko pomoci i reci kako se pomocu simbolicke metode dobije FI za Catalanove brojeve? |
Ovako nekako bi islo - nti Catalanov broj je broj najkracih puteva u cjelobrojnoj mrezi od (0, 0) do (n + 1, n + 1) bez diranja dijagonale.
Takav put moze biti ili prazan (pritom mislim na to da si vec u tocki u koju zelis doci) ili se moze opisati kao put od tocke (1, 0) do neke tocke (k + 1, k te put od tocke (k, k) do tocke (n+1, n+1), s time da oba puta zadovoljavaju prijasnji uvjet.
Sad to pises ovako:
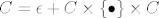
C bi trebalo biti lijepo pisano i predstavlja klasu kombinatornih objekata - puteva od tocke (0, 0) do tocaka oblika (k, k). C prelazi u FI C, epsilon u 1, "tockica" u x, pa dobijes:
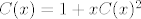 |
posve ista stvar je, a mozda malo ljepsa i razumljivija za gledat, rekurzija za binarna stabla sa n vrhova...
pokazali smo da su to iste rekurzije, pa onda razmizljas ovako: binarno stablo je ili prazno ili se sastoji od korijena i dva podstabla, koja su i sama binarna stabla 
zapis je naravno isti... pa necu ponavljat. sad reci da je ovo bolje 
|
|
| [Vrh] |
|
LSSD
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (19:11:16)
Postovi: (CB)16
Lokacija: SD CN
|
|
| [Vrh] |
|
Mishika
Forumaš(ica)

Pridružen/a: 28. 09. 2005. (11:32:36)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Mishika
Forumaš(ica)

Pridružen/a: 28. 09. 2005. (11:32:36)
Postovi: (32)16
Spol: 
|
 Postano: 14:51 pon, 1. 5. 2006 Naslov: Postano: 14:51 pon, 1. 5. 2006 Naslov: |
    |
|
|
Imam knjigu ali ono kaj je u njoj nije ono kaj meni treba. U knjizi nisam nigdje nasla konkretni dokaz na koji je nacin postavljena ova suma,uvijek je pokazano preko problema binarnih stabla, problema zagrada ,problema triangulacije konveksnog poligona.Meni nije jasno zbog cega je u sumi c(k)*c(n-k-1). Koju tocku promatramo kada dijelimo put (0,0)-(n+1,n+1) na dva dijela?
Imam knjigu ali ono kaj je u njoj nije ono kaj meni treba. U knjizi nisam nigdje nasla konkretni dokaz na koji je nacin postavljena ova suma,uvijek je pokazano preko problema binarnih stabla, problema zagrada ,problema triangulacije konveksnog poligona.Meni nije jasno zbog cega je u sumi c(k)*c(n-k-1). Koju tocku promatramo kada dijelimo put (0,0)-(n+1,n+1) na dva dijela?
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 9:30 uto, 2. 5. 2006 Naslov: Postano: 9:30 uto, 2. 5. 2006 Naslov: |
    |
|
|
[quote="Mishika"]Imam knjigu ali ono kaj je u njoj nije ono kaj meni treba. U knjizi nisam nigdje nasla konkretni dokaz na koji je nacin postavljena ova suma,uvijek je pokazano preko problema binarnih stabla, problema zagrada ,problema triangulacije konveksnog poligona.Meni nije jasno zbog cega je u sumi c(k)*c(n-k-1). Koju tocku promatramo kada dijelimo put (0,0)-(n+1,n+1) na dva dijela?[/quote]
Svih puteva od (0,0) do (n,n) ima 2n povrh n. No treba oduzeti one koje sijeku dijagonalu.To se radi tako da npr. nakon sto smo prvi put prijesli dijagonalu svaki pomak prema desno zamijenimo pomakom prema gore i obrnuto(pomak prema gore zamijeniti pomakom prema desno) .No ako smo napravili k pomaka prema desno i k+1 pomak prema gore (znaci prijesli smo dijagonalu) ostalo nam je n-k koraka prema desno i n-k-1 koraka prema gore ,no sa nasom zamjenom imamo k+(n-k-1)=n-1 pomaka prema desno i k+1 + (n-k) = n+1 pomaka prema gore.Tj. imamo put do tocke (n-1,n+1) .No tako svaki nedozvoljeni put mozemo preinaciti.
Puteva od (0,0) do (n-1,n+1) ima 2n povrh n+1,te to oduzmes i dobijes 2n povrh n - 2n povrh n+1,to ti je upravo 1/n+1 2n povrh n.(Mozes provjeriti ;jednostavno 1/n+1 2n povrh n dodaj i oduzmi n (tj. 1-n+n/n+1 ...) i raspisi i dobiti ces trazeno.
Preko dekompozicije n-terokuta , odaberes nasumicno 1 stranicu i jednu tocku "nad " stranicom. Tada ti je s jedne strane preostalo konveksni k-terkout za dekompoziciju ,a s druge strane n-k+1 -terokut za dekompozciju. Dekompozicije su medusobno nezavisne pa pomnozis i prosumiras od 2 do n-1( C(2):=1) imas C(n)=suma C(k)*C(n-k+1).
Analogno sa binarnim stablom "odvojis" korijen i dva podstabla, tada mozes imati 1 vrh s lijeve strane n-2 vrha s desne , 2 vrha s lijeve n-3 vrhova s desne.
Dobijes T(n)=suma T(k)*T(n-k-1). (T(0):=1)
Kod funkcije izvodnice f(x)=C(0) + C(1)x +... kvadriraj ,dobijes koeficijente ,no moras pomnoziti sa x da bi koeficijenti odgovarali potencijama i oduzmes C(0) buduci da ti on fali(raspisi pa ces to dobiti)
;dobijes x*F(x)^2 -F(x) +1 =0. Trazis nultocke te tvojoj FI odgovara F(x)=1/(2x) - (1-4x)^(1/2) /(2x).Trazis <x^n> o dobijes 1/n+1 2n povrh n.
| Mishika (napisa): | | Imam knjigu ali ono kaj je u njoj nije ono kaj meni treba. U knjizi nisam nigdje nasla konkretni dokaz na koji je nacin postavljena ova suma,uvijek je pokazano preko problema binarnih stabla, problema zagrada ,problema triangulacije konveksnog poligona.Meni nije jasno zbog cega je u sumi c(k)*c(n-k-1). Koju tocku promatramo kada dijelimo put (0,0)-(n+1,n+1) na dva dijela? |
Svih puteva od (0,0) do (n,n) ima 2n povrh n. No treba oduzeti one koje sijeku dijagonalu.To se radi tako da npr. nakon sto smo prvi put prijesli dijagonalu svaki pomak prema desno zamijenimo pomakom prema gore i obrnuto(pomak prema gore zamijeniti pomakom prema desno) .No ako smo napravili k pomaka prema desno i k+1 pomak prema gore (znaci prijesli smo dijagonalu) ostalo nam je n-k koraka prema desno i n-k-1 koraka prema gore ,no sa nasom zamjenom imamo k+(n-k-1)=n-1 pomaka prema desno i k+1 + (n-k) = n+1 pomaka prema gore.Tj. imamo put do tocke (n-1,n+1) .No tako svaki nedozvoljeni put mozemo preinaciti.
Puteva od (0,0) do (n-1,n+1) ima 2n povrh n+1,te to oduzmes i dobijes 2n povrh n - 2n povrh n+1,to ti je upravo 1/n+1 2n povrh n.(Mozes provjeriti ;jednostavno 1/n+1 2n povrh n dodaj i oduzmi n (tj. 1-n+n/n+1 ...) i raspisi i dobiti ces trazeno.
Preko dekompozicije n-terokuta , odaberes nasumicno 1 stranicu i jednu tocku "nad " stranicom. Tada ti je s jedne strane preostalo konveksni k-terkout za dekompoziciju ,a s druge strane n-k+1 -terokut za dekompozciju. Dekompozicije su medusobno nezavisne pa pomnozis i prosumiras od 2 do n-1( C(2):=1) imas C(n)=suma C(k)*C(n-k+1).
Analogno sa binarnim stablom "odvojis" korijen i dva podstabla, tada mozes imati 1 vrh s lijeve strane n-2 vrha s desne , 2 vrha s lijeve n-3 vrhova s desne.
Dobijes T(n)=suma T(k)*T(n-k-1). (T(0):=1)
Kod funkcije izvodnice f(x)=C(0) + C(1)x +... kvadriraj ,dobijes koeficijente ,no moras pomnoziti sa x da bi koeficijenti odgovarali potencijama i oduzmes C(0) buduci da ti on fali(raspisi pa ces to dobiti)
;dobijes x*F(x)^2 -F(x) +1 =0. Trazis nultocke te tvojoj FI odgovara F(x)=1/(2x) - (1-4x)^(1/2) /(2x).Trazis <x^n> o dobijes 1/n+1 2n povrh n.
|
|
| [Vrh] |
|
Mishika
Forumaš(ica)

Pridružen/a: 28. 09. 2005. (11:32:36)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
|











