| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 19:39 pon, 5. 6. 2006 Naslov: Postano: 19:39 pon, 5. 6. 2006 Naslov: |
    |
|
|
1. zad:
Dobijem isto kao i ti e^iz i od tuda dobijem ili za e^iz=1+sqrt2 da je x=pi*(1/2+2k), k iz Z, a y=ln(1/1+sqrt2), a za e^iz=1-sqrt2 x=pi*(3/2+2k), k iz Z, a y=ln(1/sqrt2-1) i niti jedna od tih točaka ne leži unutar danog kvadrata pa je integral jednak 0.
2. zad:
Iskoristi prvo od onih pravila za računanje reziduuma i f-ja u z=0 ima pol 2. reda pa imaš lim (sin(1/1-2z))'= lim cos(1/1-2z)*(2/(1-2z)^2)=2*cos1. A što se tiče z=1/2 to je izvan dane elipse -> integral je 4*pi*i*cos1.
Hope it helps :wink:
1. zad:
Dobijem isto kao i ti e^iz i od tuda dobijem ili za e^iz=1+sqrt2 da je x=pi*(1/2+2k), k iz Z, a y=ln(1/1+sqrt2), a za e^iz=1-sqrt2 x=pi*(3/2+2k), k iz Z, a y=ln(1/sqrt2-1) i niti jedna od tih točaka ne leži unutar danog kvadrata pa je integral jednak 0.
2. zad:
Iskoristi prvo od onih pravila za računanje reziduuma i f-ja u z=0 ima pol 2. reda pa imaš lim (sin(1/1-2z))'= lim cos(1/1-2z)*(2/(1-2z)^2)=2*cos1. A što se tiče z=1/2 to je izvan dane elipse -> integral je 4*pi*i*cos1.
Hope it helps 
|
|
| [Vrh] |
|
Gost
|
 Postano: 9:40 uto, 6. 6. 2006 Naslov: Postano: 9:40 uto, 6. 6. 2006 Naslov: |
    |
|
|
[quote]1. zad:
Dobijem isto kao i ti e^iz i od tuda dobijem ili za e^iz=1+sqrt2 da je x=pi*(1/2+2k), k iz Z, a y=ln(1/1+sqrt2), a za e^iz=1-sqrt2 x=pi*(3/2+2k), k iz Z, a y=ln(1/sqrt2-1) i niti jedna od tih točaka ne leži unutar danog kvadrata pa je integral jednak 0.
[/quote] e al ja ti ne znam to raspisat kad dobijem e^iz.. ne znam izračunat x... :oops: sva se zapetljam i ne mogu raspisat.. je ti se da napisat kak se izračuna taj x pliz??
& thank u za drugi!! :ok:
:boks2:
| Citat: | 1. zad:
Dobijem isto kao i ti e^iz i od tuda dobijem ili za e^iz=1+sqrt2 da je x=pi*(1/2+2k), k iz Z, a y=ln(1/1+sqrt2), a za e^iz=1-sqrt2 x=pi*(3/2+2k), k iz Z, a y=ln(1/sqrt2-1) i niti jedna od tih točaka ne leži unutar danog kvadrata pa je integral jednak 0.
|
e al ja ti ne znam to raspisat kad dobijem e^iz.. ne znam izračunat x...  sva se zapetljam i ne mogu raspisat.. je ti se da napisat kak se izračuna taj x pliz?? sva se zapetljam i ne mogu raspisat.. je ti se da napisat kak se izračuna taj x pliz??
& thank u za drugi!! 

|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
mea
Forumaš(ica)

Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
|
 Postano: 13:48 uto, 6. 6. 2006 Naslov: Postano: 13:48 uto, 6. 6. 2006 Naslov: |
    |
|
|
[quote="Mr.Doe"]... dobivam nesta tipa e^z/z-1 ,te dalje ne znam sta raditi sa time,da li napisati kao produkt geo. reda i razvoja eksp. f-ije :? ,ili nesta "trece".[/quote]
Ako napises kao produkt redova, izmnozis i grupiras po potencijama od z, dobivas da je koeficijent uz [latex]z^n[/latex] jednak [latex]
\sum_{k=0}^{n} {1\over k!}[/latex].
| Mr.Doe (napisa): | ... dobivam nesta tipa e^z/z-1 ,te dalje ne znam sta raditi sa time,da li napisati kao produkt geo. reda i razvoja eksp. f-ije  ,ili nesta "trece". ,ili nesta "trece". |
Ako napises kao produkt redova, izmnozis i grupiras po potencijama od z, dobivas da je koeficijent uz 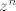 jednak jednak 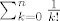 . .
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
mea
Forumaš(ica)

Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
mea
Forumaš(ica)

Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
|
|
| [Vrh] |
|
|








