Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

integral (zadatak)
WWW:

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
micika
Gost
PostPostano: 15:28 čet, 22. 6. 2006    Naslov: integral (zadatak) Citirajte i odgovorite
jedan integral s roka 19.6.2002.

(2)integral(-5) [i]sign[/i](sinx)(x-[i]sign[/i](x))dx

f-ja sign(x) koliko znam vraća -1,0,1 ovisno je li x negativan, nula ili pozitivan, ali kako raspisati ovaj integral i izračunati ga?

pomoć molim (Vjekin odgovor na pitanje bi bio više nego dovoljan :wink: )

ne znam kakve će nama vrste integrali biti... :(
jedan integral s roka 19.6.2002.

(2)integral(-5) sign(sinx)(x-sign(x))dx

f-ja sign(x) koliko znam vraća -1,0,1 ovisno je li x negativan, nula ili pozitivan, ali kako raspisati ovaj integral i izračunati ga?

pomoć molim (Vjekin odgovor na pitanje bi bio više nego dovoljan Wink )

ne znam kakve će nama vrste integrali biti... Sad


[Vrh]
Gost
PostPostano: 15:54 čet, 22. 6. 2006    Naslov: Citirajte i odgovorite
kako riješiti ovaj integral? samo hint trebam...

int (dx/sqrt(1+e^x+e^(2x)) = ?

supsitucija pa parcijalna? baš mi i ne uspijeva izvesti...
kako riješiti ovaj integral? samo hint trebam...

int (dx/sqrt(1+e^x+e^(2x)) = ?

supsitucija pa parcijalna? baš mi i ne uspijeva izvesti...


[Vrh]
hermione
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: kućni ljubimac
Sarma: -
PostPostano: 16:35 čet, 22. 6. 2006    Naslov: Citirajte i odgovorite
[quote="Anonymous"]kako riješiti ovaj integral? samo hint trebam...

int (dx/sqrt(1+e^x+e^(2x)) = ?

supsitucija pa parcijalna? baš mi i ne uspijeva izvesti...[/quote]
[latex]
\int\frac{dx}{\sqrt{1+e^x+e^{2x}}}\stackrel{supst.}{=}\int\frac{dt}{t\sqrt{1+t+t^2}}=\\
\int\frac{dt}{t\sqrt{(t+\frac{1}{2})^2+\frac{3}{4}}}[/latex] i sada dalje supstitucija
Anonymous (napisa):
kako riješiti ovaj integral? samo hint trebam...

int (dx/sqrt(1+e^x+e^(2x)) = ?

supsitucija pa parcijalna? baš mi i ne uspijeva izvesti...

i sada dalje supstitucija



_________________
http://www.youtube.com/watch?v=SjN_4LO-5L8

U tijelu nema pravih ideala

Zadnja promjena: hermione; 16:59 čet, 22. 6. 2006; ukupno mijenjano 2 put/a.
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
Gost
PostPostano: 16:57 čet, 22. 6. 2006    Naslov: Citirajte i odgovorite
joj, fala, to sam i dobila, i nisam se sjetila za taj Arsh, a jos je i na tablici naveden...
joj, fala, to sam i dobila, i nisam se sjetila za taj Arsh, a jos je i na tablici naveden...


[Vrh]
vjekovac
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
182 = 198 - 16
PostPostano: 20:18 čet, 22. 6. 2006    Naslov: Re: integral (zadatak) Citirajte i odgovorite
[quote="micika"]jedan integral s roka 19.6.2002.
(...) Vjekin odgovor na pitanje bi bio više nego dovoljan[/quote]
Pa kad sam već ovako javno prozvan... :lol:

[latex]\int\limits_{-5}^{2}\mathrm{sign}(\sin x)(x-\mathrm{sign}\,x)\,dx[/latex]

Naprije se prisjetimo gdje je sin pozitivan, a gdje negativan te primijetimo [latex]-5<-\pi<0<2[/latex]

Sada je
[latex]
\mathrm{sign}(\sin x)=\left\{\begin{array}{cl}
-1, & \textrm{ za }x\in\langle -\pi,0\rangle\\
1, & \textrm{ za }x\in\langle -5,-\pi\rangle\cup\langle 0,2\rangle
\end{array}\right.
[/latex]
Vrijednost 0 se poprima za nekoliko točaka, ali nam za integriranje tih konačno mnogo točaka nije niti važno.

Dakle, rastavljamo integral ovako:
[latex]\int\limits_{-5}^{2}=\int\limits_{-5}^{-\pi}
+\int\limits_{-\pi}^{0}+\int\limits_{0}^{2}[/latex]
odnosno preciznije
[latex]\int\limits_{-5}^{2}\mathrm{sign}(\sin x)(x-\mathrm{sign}\,x)\,dx=\\
\int\limits_{-5}^{-\pi}1\cdot(x+1)\,dx+
\int\limits_{-\pi}^{0}(-1)\cdot(x+1)\,dx+
\int\limits_{0}^{2}1\cdot(x-1)\,dx=\\
=\pi^2-2\pi-\frac{15}{2}[/latex]
micika (napisa):
jedan integral s roka 19.6.2002.
(...) Vjekin odgovor na pitanje bi bio više nego dovoljan

Pa kad sam već ovako javno prozvan... Laughing



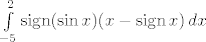
Naprije se prisjetimo gdje je sin pozitivan, a gdje negativan te primijetimo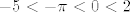

Sada je

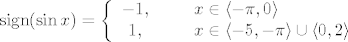
Vrijednost 0 se poprima za nekoliko točaka, ali nam za integriranje tih konačno mnogo točaka nije niti važno.

Dakle, rastavljamo integral ovako:

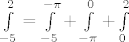
odnosno preciznije


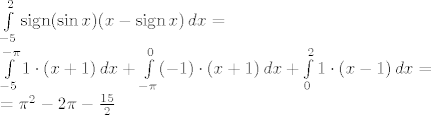
[Vrh]
Korisnički profil Pošaljite privatnu poruku Posjetite Web stranice
vjekovac
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
182 = 198 - 16
PostPostano: 20:24 čet, 22. 6. 2006    Naslov: Citirajte i odgovorite
[latex]\displaystyle\int\frac{dx}{\sqrt{1+e^x+e^{2x}}}[/latex]
Ovako kako je riješila hermie je baš kako treba i kako bi svatko razuman(?!) krenuo rješavati,
ali začudo može još malo jednostavnije supstitucijom [latex]t=e^{-x}[/latex].
Dobije se
[latex]\displaystyle-\int\frac{dt}{\sqrt{t^2+t+1}}[/latex]

Ovako kako je riješila hermie je baš kako treba i kako bi svatko razuman(?!) krenuo rješavati,
ali začudo može još malo jednostavnije supstitucijom .
Dobije se


[Vrh]
Korisnički profil Pošaljite privatnu poruku Posjetite Web stranice
hermione
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: kućni ljubimac
Sarma: -
PostPostano: 22:05 čet, 22. 6. 2006    Naslov: Citirajte i odgovorite
[quote="vjekovac"][latex]\displaystyle\int\frac{dx}{\sqrt{1+e^x+e^{2x}}}[/latex]
Ovako kako je riješila hermie je baš kako treba i kako bi svatko razuman(?!) krenuo rješavati,
ali začudo može još malo jednostavnije supstitucijom [latex]t=e^{-x}[/latex].
Dobije se
[latex]\displaystyle-\int\frac{dt}{\sqrt{t^2+t+1}}[/latex][/quote]

[latex]
\int\frac{dt}{\sqrt{1+t+t^2}}=\\ \int\frac{dt}{\sqrt{(t+\frac{1}{2})^2+\frac{3}{4}}}\stackrel{tabl.int.}{=}\\
\mathop{Arsh}\frac{t+\frac{1}{2}}{\frac{\sqrt 3}{2}}=\mathop{Arsh}\frac{2t+1}{\sqrt 3}[/latex] i dalje trivijalno...
vjekovac (napisa):

Ovako kako je riješila hermie je baš kako treba i kako bi svatko razuman(?!) krenuo rješavati,
ali začudo može još malo jednostavnije supstitucijom .
Dobije se


i dalje trivijalno...



_________________
http://www.youtube.com/watch?v=SjN_4LO-5L8

U tijelu nema pravih ideala
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2 Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan