|
Je, ciklička je. Evo tri pogleda na tu stvar koja su u suštini ista i svode se na u parovima relativnu prostost brojeva 3, 4 i 5:
[list=1]
[*]Red elementa [latex](x,y,z)[/latex] je najmanji zajednički višekratnik redova elementa [latex]x[/latex] u [latex]\mathbb{Z}_3[/latex], [latex]y[/latex] u [latex]\mathbb{Z}_4[/latex] i [latex]z[/latex] u [latex]\mathbb{Z}_5[/latex]. (Dokaži!) Prema tome, red elementa [latex](1,1,1)[/latex] je najmanji zajednički višekratnik od 3, 4 i 5, što je 60. No tad [latex]G[/latex] ima cikličku podgrupu reda 60, a kako je i sama reda 60, mora upravo [latex]G[/latex] biti ta ciklička podgrupa.
[*]Općenito, ako su [latex]m[/latex] i [latex]n[/latex] relativno prosti, onda je [latex]\mathbb{Z}_m\oplus\mathbb{Z}_n\cong\mathbb{Z}_{mn}[/latex]. Da bi se to dokazalo, pogleda se funkcija [latex]f\colon\mathbb{Z}_m\oplus\mathbb{Z}_n\to\mathbb{Z}_{mn}[/latex] zadana s [latex]f(x,y)=nx+my[/latex]. Lagano je za provjeriti da se radi o homomorfizmu.
Iz činjenice da su [latex]m[/latex] i [latex]n[/latex] relativno prosti slijedi da postoje cijeli brojevi [latex]a[/latex] i [latex]b[/latex] takvi da je [latex]am+bn=1[/latex]. Uzmimo proizvoljan [latex]k[/latex] iz [latex]\mathbb{Z}_{mn}[/latex], tad je
[latex]f(bk,ak)=nbk+mak=(am+bn)k=k[/latex]
Slijedi da je [latex]f[/latex] epimorfizam. Kako se radi o surjekciji dva konačna skupa istog kardinalnog broja, [latex]f[/latex] je i injekcija, tj. [latex]f[/latex] je izomorfizam.
Primijenimo ovo na zadani zadatak:
[latex]\mathbb{Z}_3\oplus\mathbb{Z}_4\oplus\mathbb{Z}_5\cong\mathbb{Z}_{12}\oplus\mathbb{Z}_5\cong\mathbb{Z}_{60}[/latex]
[*]Slično kao u dokazu prethodne općenite tvrdnje, pokažimo da je [latex]f\colon\mathbb{Z}_3\oplus\mathbb{Z}_4\oplus\mathbb{Z}_5\to\mathbb{Z}_{60}[/latex] zadana s [latex]f(x,y,z)=20x+15y+12z[/latex] izomorfizam. (Nadam se da je jasno otkud ovi koeficijenti.) Opet se lako provjeri da je to homomorfizam.
Budući da su 20, 15 i 12 relativno prosti, postoje cijeli brojevi [latex]a, b, c[/latex] takvi da je [latex]20a+15b+12c=1[/latex]. Konkretno, [latex]a=-1, b=3, c=-2[/latex]. Dakle, za proizvoljan [latex]k\in\mathbb{Z}_{60}[/latex] imamo:
[latex]f(-k,3k,-2k)=-20k+15\cdot 3k-12\cdot 2k=k[/latex]
Pa je [latex]f[/latex] surjekcija, a onda i bijekcija.
[/list:o]
Je, ciklička je. Evo tri pogleda na tu stvar koja su u suštini ista i svode se na u parovima relativnu prostost brojeva 3, 4 i 5:
- Red elementa
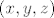 je najmanji zajednički višekratnik redova elementa je najmanji zajednički višekratnik redova elementa  u u 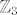 , ,  u u 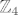 i i  u u 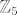 . (Dokaži!) Prema tome, red elementa . (Dokaži!) Prema tome, red elementa 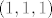 je najmanji zajednički višekratnik od 3, 4 i 5, što je 60. No tad je najmanji zajednički višekratnik od 3, 4 i 5, što je 60. No tad  ima cikličku podgrupu reda 60, a kako je i sama reda 60, mora upravo ima cikličku podgrupu reda 60, a kako je i sama reda 60, mora upravo  biti ta ciklička podgrupa. biti ta ciklička podgrupa.
- Općenito, ako su
 i i  relativno prosti, onda je relativno prosti, onda je 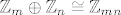 . Da bi se to dokazalo, pogleda se funkcija . Da bi se to dokazalo, pogleda se funkcija 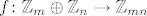 zadana s zadana s  . Lagano je za provjeriti da se radi o homomorfizmu. . Lagano je za provjeriti da se radi o homomorfizmu.
Iz činjenice da su  i i  relativno prosti slijedi da postoje cijeli brojevi relativno prosti slijedi da postoje cijeli brojevi  i i 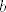 takvi da je takvi da je 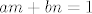 . Uzmimo proizvoljan . Uzmimo proizvoljan  iz iz 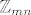 , tad je , tad je
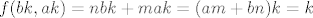
Slijedi da je  epimorfizam. Kako se radi o surjekciji dva konačna skupa istog kardinalnog broja, epimorfizam. Kako se radi o surjekciji dva konačna skupa istog kardinalnog broja,  je i injekcija, tj. je i injekcija, tj.  je izomorfizam. je izomorfizam.
Primijenimo ovo na zadani zadatak:
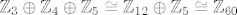
- Slično kao u dokazu prethodne općenite tvrdnje, pokažimo da je
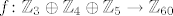 zadana s zadana s 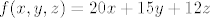 izomorfizam. (Nadam se da je jasno otkud ovi koeficijenti.) Opet se lako provjeri da je to homomorfizam. izomorfizam. (Nadam se da je jasno otkud ovi koeficijenti.) Opet se lako provjeri da je to homomorfizam.
Budući da su 20, 15 i 12 relativno prosti, postoje cijeli brojevi 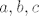 takvi da je takvi da je 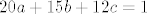 . Konkretno, . Konkretno, 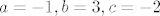 . Dakle, za proizvoljan . Dakle, za proizvoljan 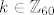 imamo: imamo:
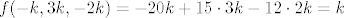
Pa je  surjekcija, a onda i bijekcija. surjekcija, a onda i bijekcija.
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|





