| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
 Postano: 15:07 sub, 18. 11. 2006 Naslov: linearni operator Postano: 15:07 sub, 18. 11. 2006 Naslov: linearni operator |
    |
|
|
1. obavezna zadaca (3.11.2005.)
Zadan je linearni operator T: V^2(O)->V^2(O) koji vektor najprije zrcali obzirom na x-os, zatim ga ortogonalno prijicira na y-os, te ga rotira za kut 2pi/3 oko ishodista u pozitivnom smjeru. Odredite:
(a) matricni zapis linearnog operatora T u standardnoj bazi {i, j}
(b) matricni zapis linearnog operatora T u bazi {2i+j, i+2j}
(c) T(xi + yj) za proizvoljni vektor xi +yj element od V^2(O)
(i, j su jedinicni vektori)
kako se rjesava takav zad?znam da ide nesto sa matricama koje su oblika
cos fi -sin fi
sin fi cos fi
na tim vjezbama sam malo zaspao i nisam pohvatao kak se rjesava.... :oops:
helpic :!:
1. obavezna zadaca (3.11.2005.)
Zadan je linearni operator T: V^2(O)->V^2(O) koji vektor najprije zrcali obzirom na x-os, zatim ga ortogonalno prijicira na y-os, te ga rotira za kut 2pi/3 oko ishodista u pozitivnom smjeru. Odredite:
(a) matricni zapis linearnog operatora T u standardnoj bazi {i, j}
(b) matricni zapis linearnog operatora T u bazi {2i+j, i+2j}
(c) T(xi + yj) za proizvoljni vektor xi +yj element od V^2(O)
(i, j su jedinicni vektori)
kako se rjesava takav zad?znam da ide nesto sa matricama koje su oblika
cos fi -sin fi
sin fi cos fi
na tim vjezbama sam malo zaspao i nisam pohvatao kak se rjesava.... 
helpic 
|
|
| [Vrh] |
|
venovako
Forumaš(ica)

Pridružen/a: 07. 11. 2002. (22:46:38)
Postovi: (2F9)16
|
 Postano: 16:49 sub, 18. 11. 2006 Naslov: Postano: 16:49 sub, 18. 11. 2006 Naslov: |
    |
|
|
Matrica rotacije za kut [latex]\phi[/latex] u kanonskoj bazi:
[latex]\displaystyle\left[\begin{array}{cc}\cos\phi&-\sin\phi\\\sin\phi&\cos\phi\end{array}\right][/latex]
Matrica zrcaljenja oko [latex]x[/latex]-osi u kanonskoj bazi:
[latex]\displaystyle\left[\begin{array}{cc}1&0\\0&-1\end{array}\right][/latex]
Matrica projektora na [latex]y[/latex]-os u kanonskoj bazi:
[latex]\displaystyle\left[\begin{array}{cc}0&0\\0&1\end{array}\right][/latex]
Prijelaz iz baze [latex](e)[/latex] u bazu [latex](f)[/latex] za matricu [latex]M[/latex] u bazi [latex](e)[/latex]:
[latex]I(f,e)M(e,e)I(e,f)=M(f,f)[/latex]
[latex]I(e,f)[/latex] matricni je prikaz identitete (operatora [latex]I(x)=x[/latex]) u paru baza [latex](e,f)[/latex], gdje je [latex](f)[/latex] je "polazna", a [latex](e)[/latex] "odredisna" baza.
Ako ti je ova recenica jasna, onda ti je jasno zasto vrijedi [latex]I(f,e)I(e,f)=I(f,f)[/latex] i [latex]I(e,f)I(f,e)=I(e,e)[/latex], tj. [latex]I(f,e)=I(e,f)^{-1}[/latex].
Naravno, za svaku bazu [latex](g)[/latex] vrijedi:
[latex]I(g,g)=\displaystyle\left[\begin{array}{cc}1&0\\0&1\end{array}\right][/latex]
Razmisli zasto je to tako i kombiniraj, tu ti je sve (do na invertiranje 2x2 matrica i primjenu matrice na vektor) za rijesiti zadatak.
Zapamti: na vektor u nekoj bazi moras primijeniti matricu u istoj toj bazi!
Ispricavam se ako sam stogod krivo napisao, davno je to bilo...
Matrica rotacije za kut 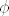 u kanonskoj bazi: u kanonskoj bazi:
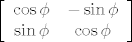
Matrica zrcaljenja oko  -osi u kanonskoj bazi: -osi u kanonskoj bazi:
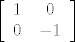
Matrica projektora na  -os u kanonskoj bazi: -os u kanonskoj bazi:
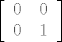
Prijelaz iz baze 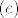 u bazu u bazu 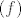 za matricu za matricu  u bazi u bazi 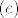 : :
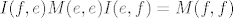
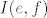 matricni je prikaz identitete (operatora matricni je prikaz identitete (operatora 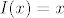 ) u paru baza ) u paru baza 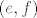 , gdje je , gdje je 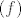 je "polazna", a je "polazna", a 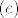 "odredisna" baza. "odredisna" baza.
Ako ti je ova recenica jasna, onda ti je jasno zasto vrijedi 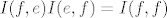 i i 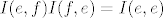 , tj. , tj. 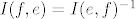 . .
Naravno, za svaku bazu 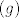 vrijedi: vrijedi:
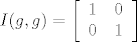
Razmisli zasto je to tako i kombiniraj, tu ti je sve (do na invertiranje 2x2 matrica i primjenu matrice na vektor) za rijesiti zadatak.
Zapamti: na vektor u nekoj bazi moras primijeniti matricu u istoj toj bazi!
Ispricavam se ako sam stogod krivo napisao, davno je to bilo...
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 20:42 ned, 19. 11. 2006 Naslov: Postano: 20:42 ned, 19. 11. 2006 Naslov: |
    |
|
|
[quote="13_mac"]mozes to malo bolje razjasnit?[/quote]
[quote="venovako"]
Matrica rotacije za kut [latex]\phi[/latex] u kanonskoj bazi:
[latex]\displaystyle\left[\begin{array}{cc}\cos\phi&-\sin\phi\\\sin\phi&\cos\phi\end{array}\right][/latex]
[/quote]
Dakle, tako izgleda matrica rotacije za proizvoljni kut [latex]\phi[/latex].
Ako ti npr. treba matrica rotacije za [latex]\frac{\pi}{2}[/latex], onda uvrstis [latex]\phi=\frac{\pi}{2}[/latex] i vidis da ti matrica rotacije za[latex]\frac{\pi}{2}[/latex] glasi:
[latex]\displaystyle
\left[ \begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right]
[/latex]
[quote="venovako"]
Matrica zrcaljenja oko [latex]x[/latex]-osi u kanonskoj bazi:
[latex]\displaystyle\left[\begin{array}{cc}1&0\\0&-1\end{array}\right][/latex]
[/quote]
Ovo gore je matrica zrcaljenja i to nije specijalni slucaj matrice rotacije, tj. ne dobiva se tako da se u prethodnu formulu umjesto [latex]\phi[/latex] uvrsti neki konkretan kut. Razlog tome je sto zrcaljenje ne mozes prikazati kao rotaciju za neki odredjeni kut.
Analogno, ni matrica projektora nije specijalan slucaj matrice rotacije, jer se projekcija ne moze prikazati kao rotacija za neki kut.
HTH
| 13_mac (napisa): | | mozes to malo bolje razjasnit? |
| venovako (napisa): |
Matrica rotacije za kut 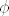 u kanonskoj bazi: u kanonskoj bazi:
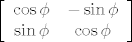
|
Dakle, tako izgleda matrica rotacije za proizvoljni kut 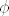 . .
Ako ti npr. treba matrica rotacije za 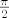 , onda uvrstis , onda uvrstis  i vidis da ti matrica rotacije za i vidis da ti matrica rotacije za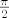 glasi: glasi:
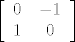
| venovako (napisa): |
Matrica zrcaljenja oko  -osi u kanonskoj bazi: -osi u kanonskoj bazi:
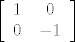
|
Ovo gore je matrica zrcaljenja i to nije specijalni slucaj matrice rotacije, tj. ne dobiva se tako da se u prethodnu formulu umjesto 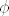 uvrsti neki konkretan kut. Razlog tome je sto zrcaljenje ne mozes prikazati kao rotaciju za neki odredjeni kut. uvrsti neki konkretan kut. Razlog tome je sto zrcaljenje ne mozes prikazati kao rotaciju za neki odredjeni kut.
Analogno, ni matrica projektora nije specijalan slucaj matrice rotacije, jer se projekcija ne moze prikazati kao rotacija za neki kut.
HTH
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
GauSs_
Moderator


Pridružen/a: 28. 01. 2004. (21:01:17)
Postovi: (53C)16
Spol: 
Lokacija: 231
|
 Postano: 9:17 pon, 20. 11. 2006 Naslov: Postano: 9:17 pon, 20. 11. 2006 Naslov: |
    |
|
|
matrica zrcaljenja (za x os):
e1=(1,0) se preslikava u e1=(1,0) -> Ae1=e1=1*e1+0*e2
e2=(0,1) se preslikava u -e2=(0,-1) -> Ae2=-e2=0*e1+(-1)*e2
matrica linearnog operatora se radi tako da po stupcima
stavljas koeficijente uz clanove baze kod Ae1, Ae2, (... , za vise dimenzija)
iz gore napisanog vidimo da su to koeficijenti 1, 0, 0, -1
sada slijedi:
[latex]
\displaystyle
A=\left[ \begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]
[/latex]
matrica zrcaljenja (za x os):
e1=(1,0) se preslikava u e1=(1,0) → Ae1=e1=1*e1+0*e2
e2=(0,1) se preslikava u -e2=(0,-1) → Ae2=-e2=0*e1+(-1)*e2
matrica linearnog operatora se radi tako da po stupcima
stavljas koeficijente uz clanove baze kod Ae1, Ae2, (... , za vise dimenzija)
iz gore napisanog vidimo da su to koeficijenti 1, 0, 0, -1
sada slijedi:
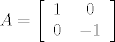
_________________ The purpose of life is to end

Prosle su godine kolokviji bili laksi, zar ne? |
|
| [Vrh] |
|
|












