| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
plavooka malena
Forumaš(ica)
Pridružen/a: 25. 07. 2006. (11:32:40)
Postovi: (4E)16
|
|
| [Vrh] |
|
tp
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (16:46:01)
Postovi: (1F2)16
|
 Postano: 22:30 čet, 2. 11. 2006 Naslov: Postano: 22:30 čet, 2. 11. 2006 Naslov: |
    |
|
|
[quote="[url=http://web.math.hr/nastava/em/]web stranica kolegija[/url]"]Student će tokom semestra dobiti 6 domaćih zadaća, čija rješenja treba predati osobno svom asistentu najkasnije 14 dana od primitka zadaće, i to u terminu vježbi. Ukoliko student tokom semestra redovito pohađa predavanja i vježbe te preda barem 3 zadaće u kojima je riješio barem 50% zadataka (u svakoj zadaći) dobija 5 bodova, a student koji tokom semestra redovito pohađa predavanja i vježbe te preda barem 5 zadaća u kojima je riješio barem 50% zadataka (u svakoj zadaći) dobija 10 bodova.[/quote]
S obzirom na navedeno ja [i]najvjerojatnije[/i] necu objavljivati rezultate zadaca.
Mozda ce drugi asistenti raditi drugacije za svoju grupu.
Ako ste napravili barem 50% zadataka na zadaci dobijete plus i to je to, a na kraju cete vidjeti koliko imate pluseva. Ako iz nekog razloga zelite vidjeti i prodiskutirati svoju zadacu, uvijek mozete doci na konzultacije. Ovo sve, naravno, vrijedi ako ste u mojoj grupi.
Tomislav Pejkovic
| web stranica kolegija (napisa): | | Student će tokom semestra dobiti 6 domaćih zadaća, čija rješenja treba predati osobno svom asistentu najkasnije 14 dana od primitka zadaće, i to u terminu vježbi. Ukoliko student tokom semestra redovito pohađa predavanja i vježbe te preda barem 3 zadaće u kojima je riješio barem 50% zadataka (u svakoj zadaći) dobija 5 bodova, a student koji tokom semestra redovito pohađa predavanja i vježbe te preda barem 5 zadaća u kojima je riješio barem 50% zadataka (u svakoj zadaći) dobija 10 bodova. |
S obzirom na navedeno ja najvjerojatnije necu objavljivati rezultate zadaca.
Mozda ce drugi asistenti raditi drugacije za svoju grupu.
Ako ste napravili barem 50% zadataka na zadaci dobijete plus i to je to, a na kraju cete vidjeti koliko imate pluseva. Ako iz nekog razloga zelite vidjeti i prodiskutirati svoju zadacu, uvijek mozete doci na konzultacije. Ovo sve, naravno, vrijedi ako ste u mojoj grupi.
Tomislav Pejkovic
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
vinko
Forumaš(ica)

Pridružen/a: 26. 08. 2006. (23:08:00)
Postovi: (1A8)16
Spol: 
Lokacija: PMF-MO 214
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
tp
Forumaš(ica)

Pridružen/a: 05. 12. 2005. (16:46:01)
Postovi: (1F2)16
|
|
| [Vrh] |
|
The Economist
Forumaš(ica)


Pridružen/a: 04. 06. 2006. (00:03:21)
Postovi: (5D)16
Spol: 
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
|
| [Vrh] |
|
vinko
Forumaš(ica)

Pridružen/a: 26. 08. 2006. (23:08:00)
Postovi: (1A8)16
Spol: 
Lokacija: PMF-MO 214
|
|
| [Vrh] |
|
vinko
Forumaš(ica)

Pridružen/a: 26. 08. 2006. (23:08:00)
Postovi: (1A8)16
Spol: 
Lokacija: PMF-MO 214
|
 Postano: 23:02 sri, 3. 1. 2007 Naslov: Re: 4.zadaca Postano: 23:02 sri, 3. 1. 2007 Naslov: Re: 4.zadaca |
    |
|
|
[quote="ivanzub"]
2. Dokazite da je mn(m^4-n^4) djeljivo s 15 za sve m,n element od N.[/quote]
Budući je 3*5=15, trebamo dokazati da je gornji izraz djeljiv i sa 3 i sa 5.
Pogledajmo npr. 5:
Ako je m ili n djeljiv sa 5, onda je i cijeli izraz djeljiv sa 5. U protivnom promotrimo m^4-n^4. Po Malom Fermatovom Teoremu (ili provjerom 'na prste') m^4 daje ostatak 1 pri djeljenju sa 5, a i n^4, pa razlika ta dva broja daje ostatak 0, tj. djeljiva je s 5. Prema tome, i taj umnožak je djeljiv s 5.
Sa 3 je jednako...
(Isto je i m^4-n^4 djeljivo s 3 (jer m^2 daje ostatak 1 pri djeljenju s 3, pa onda i m^2^2=m^4)...)
| ivanzub (napisa): |
2. Dokazite da je mn(m^4-n^4) djeljivo s 15 za sve m,n element od N. |
Budući je 3*5=15, trebamo dokazati da je gornji izraz djeljiv i sa 3 i sa 5.
Pogledajmo npr. 5:
Ako je m ili n djeljiv sa 5, onda je i cijeli izraz djeljiv sa 5. U protivnom promotrimo m^4-n^4. Po Malom Fermatovom Teoremu (ili provjerom 'na prste') m^4 daje ostatak 1 pri djeljenju sa 5, a i n^4, pa razlika ta dva broja daje ostatak 0, tj. djeljiva je s 5. Prema tome, i taj umnožak je djeljiv s 5.
Sa 3 je jednako...
(Isto je i m^4-n^4 djeljivo s 3 (jer m^2 daje ostatak 1 pri djeljenju s 3, pa onda i m^2^2=m^4)...)
Zadnja promjena: vinko; 9:59 čet, 4. 1. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
erzsebet
Forumaš(ica)
Pridružen/a: 04. 10. 2006. (18:04:17)
Postovi: (20)16
Spol: 
|
 Postano: 8:45 čet, 4. 1. 2007 Naslov: 4. zadaca (pomoc) Postano: 8:45 čet, 4. 1. 2007 Naslov: 4. zadaca (pomoc) |
    |
|
|
Ako tko ima volje pomagati, bila bih zahvalna... Ono, X-mas spirit i sve to.... :D
1. Dokazite da za skupove A1,...,An vrijedi De Morganov teorem:
(Unija od i=1 do n po Ai) sve komplementirano == presjek od i=1 do n po Ai komplement.
tj. (A1UA2U...UAi)komplement=A1kompl. presjek A2kompl. presjek......Aikompl.
12. Indukcijom dokazi da za svaki prirodan br. n>1, broj (2^(2^n))
(iliti 2 na kvadrat, a kvadrat na n-tu potenciju) zavrsava sa 6
ps. unaprijed isprika zbog nezgodno (ruzno) postavljenih pitanja
Ako tko ima volje pomagati, bila bih zahvalna... Ono, X-mas spirit i sve to.... 
1. Dokazite da za skupove A1,...,An vrijedi De Morganov teorem:
(Unija od i=1 do n po Ai) sve komplementirano == presjek od i=1 do n po Ai komplement.
tj. (A1UA2U...UAi)komplement=A1kompl. presjek A2kompl. presjek......Aikompl.
12. Indukcijom dokazi da za svaki prirodan br. n>1, broj (2^(2^n))
(iliti 2 na kvadrat, a kvadrat na n-tu potenciju) zavrsava sa 6
ps. unaprijed isprika zbog nezgodno (ruzno) postavljenih pitanja
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 9:29 čet, 4. 1. 2007 Naslov: Postano: 9:29 čet, 4. 1. 2007 Naslov: |
    |
|
|
1. Asocijativnost presjeka odnosno unije + indukcija. :D
12. Nije "2 na kvadrat, a kvadrat na n-tu potenciju" nego "2 na x, gdje x oznacava 2 na n-tu". :)
Korak indukcije:
[latex]2^{2^{n+1}} = 2^{2 \cdot 2^n} = (2^{2^n})^2[/latex]
Ostaje za provjeriti za n=2 (sto je [latex]2^{2^2} = 2^4 = 16[/latex]) i pokazati da ako [i]x[/i] zavrsava sesticom, onda i [latex]x^2[/latex] zavrsava sesticom (ovo ide trivijalnim raspisom x=10a+b, b€{0,1,...,9}). 8)
1. Asocijativnost presjeka odnosno unije + indukcija. 
12. Nije "2 na kvadrat, a kvadrat na n-tu potenciju" nego "2 na x, gdje x oznacava 2 na n-tu". 
Korak indukcije:
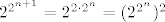
Ostaje za provjeriti za n=2 (sto je 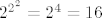 ) i pokazati da ako x zavrsava sesticom, onda i ) i pokazati da ako x zavrsava sesticom, onda i 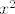 zavrsava sesticom (ovo ide trivijalnim raspisom x=10a+b, b€{0,1,...,9}). zavrsava sesticom (ovo ide trivijalnim raspisom x=10a+b, b€{0,1,...,9}). 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 11:49 čet, 4. 1. 2007 Naslov: Postano: 11:49 čet, 4. 1. 2007 Naslov: |
    |
|
|
Evo ga u attachmentu.
Evo ga u attachmentu.
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
| Description: |
|

Download |
| Filename: |
06em1dz4.pdf |
| Filesize: |
140.16 KB |
| Downloaded: |
288 Time(s) |
|
|
| [Vrh] |
|
The Economist
Forumaš(ica)


Pridružen/a: 04. 06. 2006. (00:03:21)
Postovi: (5D)16
Spol: 
|
|
| [Vrh] |
|
Nori
Forumaš(ica)
Pridružen/a: 01. 10. 2006. (18:41:07)
Postovi: (E5)16
Spol: 
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
the maja
Forumaš(ica)

Pridružen/a: 26. 11. 2006. (09:35:27)
Postovi: (5D)16
Spol: 
Lokacija: Zagreb
|
 Postano: 11:56 ned, 21. 1. 2007 Naslov: Postano: 11:56 ned, 21. 1. 2007 Naslov: |
    |
|
|
ja mislim da se riješava ovako: nađeš stupanj polinoma tako da uzmeš da je st(p(x))=n, pa izjednačiš lijevu i desnu stranu i dobiješ n=2, što znači da polinom u općem obliku izgleda ax^2 + bx + c, i onda ga samo uvrstiš u početnu jednadžu, izjednačavaš koeficijente, i dobiješ tako riješenje. :)
ja mislim da se riješava ovako: nađeš stupanj polinoma tako da uzmeš da je st(p(x))=n, pa izjednačiš lijevu i desnu stranu i dobiješ n=2, što znači da polinom u općem obliku izgleda ax^2 + bx + c, i onda ga samo uvrstiš u početnu jednadžu, izjednačavaš koeficijente, i dobiješ tako riješenje. 
|
|
| [Vrh] |
|
|

















