| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
 Postano: 0:33 ned, 18. 2. 2007 Naslov: Postano: 0:33 ned, 18. 2. 2007 Naslov: |
    |
|
|
Ne nisi. Puno ti hvala. Jedan dio sam sam shvatio; zasto umjesto E[X[size=3]n[/size]/n] u izraz za limes niza vjeroatnosti uvrstavamo p. Naime, zbog linearnosti ocekivanja E[X[size=3]n[/size]/n]=1/n E[X[size=3]n[/size]], a kako je X[size=3]n[/size] binomna, ocekivanje joj je np (za svaki n€N). Dakle je 1/n E[X[size=3]n[/size]] = 1/n np = p. Dakle ocekivanje od X[size=3]n[/size]/n (a to je 'nova' slucajna varijabla koju uvrstavamo u Čebišeljejeva) ne ovisi o n, pa mozemo uvrstiti p.
Jos jednom, hvala nana :kisscheek: .
Kad nam je vec tako dobro krenulo, bi mi znao netko razjasniti jedan dio Weierstrassov-og teorema;
[latex]\le \sum_{\{k:|\frac{k}{n}-p|<\delta\}} |g(p)-g(\frac{k}{n})| \left( \begin{array}{1} n \\ k \\ \end{array} \right) p^k q^{n - k}[/latex] [latex]+\sum_{\{k:|\frac{k}{n}-p| \ge \delta\}} |g(p)-g(\frac{k}{n})| \left( \begin{array}{1} n \\ k \\ \end{array} \right) p^k q^{n - k}\le[/latex]
Tu se kaze da je [latex]|g(p)-g(\frac{k}{n})|<\varepsilon[/latex], a [latex]\left( \begin{array}{1} n \\ k \\ \end{array} \right) p^k q^{n - k}\le1[/latex] u prvoj sumi. E sad, kako se odavde dode do toga da je ta cijela prva suma manja od [latex]\varepsilon[/latex]??
Ne nisi. Puno ti hvala. Jedan dio sam sam shvatio; zasto umjesto E[Xn/n] u izraz za limes niza vjeroatnosti uvrstavamo p. Naime, zbog linearnosti ocekivanja E[Xn/n]=1/n E[Xn], a kako je Xn binomna, ocekivanje joj je np (za svaki n€N). Dakle je 1/n E[Xn] = 1/n np = p. Dakle ocekivanje od Xn/n (a to je 'nova' slucajna varijabla koju uvrstavamo u Čebišeljejeva) ne ovisi o n, pa mozemo uvrstiti p.
Jos jednom, hvala nana  . .
Kad nam je vec tako dobro krenulo, bi mi znao netko razjasniti jedan dio Weierstrassov-og teorema;
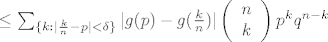 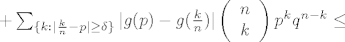
Tu se kaze da je 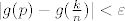 , a , a 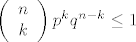 u prvoj sumi. E sad, kako se odavde dode do toga da je ta cijela prva suma manja od u prvoj sumi. E sad, kako se odavde dode do toga da je ta cijela prva suma manja od  ?? ??
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 18:44 ned, 18. 2. 2007 Naslov: Postano: 18:44 ned, 18. 2. 2007 Naslov: |
    |
|
|
[url]http://en.wikipedia.org/wiki/Weierstrass_theorem[/url] :
In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function.
Umjesto ove općenitije tvrdnje, mi smo pokazali da vrijedi da se funkcija [latex]g:\left[ {0,1} \right] \to {\bf R}[/latex] može uniformno aproksimirati nizom Bernsteineovih polinoma, što zapravo znači da niz funkcija [latex]B_n[/latex] uniformno konvergira prema funkciji [latex]g[/latex], odnosno [latex]\left( {\forall \varepsilon > 0} \right)\left( {\exists n_0 \in {\bf N}} \right)\left( {\forall n \ge n_0 } \right)\left( {\forall p \in \left[ {0,1} \right]} \right)\left( {\left| {B_n \left( p \right) - g\left( p \right)} \right| < \varepsilon } \right)[/latex]. Ako pogledamo gornji zapis, vidimo da ako smanjujemo [latex]\varepsilon[/latex], [latex]n_0[/latex] će općenito rasti.
Fiksirajmo si neki [latex]n[/latex] i pogledajmo [latex]\mathop {\max }\limits_{p \in \left[ {0,1} \right]} \left\{ {\left| {B_n \left( p \right) - g\left( p \right)} \right|} \right\}[/latex]. E sad, definicija uniformne konvergencije niza Bernsteinovih polinoma prema [latex]g[/latex] ti garantira da će se i najveći razmak [latex]{\left| {B_n \left( p \right) - g\left( p \right)} \right|}[/latex] smanjit na manje od [latex]\varepsilon[/latex] nakon nekog [latex]n[/latex] za [latex]p \in \left[ {0,1} \right][/latex], što možeš napisat i kao [latex]\left( {\forall \varepsilon > 0} \right)\left( {\exists n_0 \in {\bf N}} \right)\left( {\forall n \ge n_0 } \right)\left( {\left| {\mathop {\max }\limits_{p \in \left[ {0,1} \right]} \left\{ {\left| {B_n \left( p \right) - g\left( p \right)} \right|} \right\} - 0} \right| < \varepsilon } \right) \Leftrightarrow[/latex][latex]\mathop {\lim }\limits_{n \to \infty } \left( {\mathop {\max }\limits_{p \in \left[ {0,1} \right]} \left\{ {\left| {B_n \left( p \right) - g\left( p \right)} \right|} \right\}} \right) = 0[/latex] (ovo gore je definicija limesa niza [latex]{\mathop {\max }\limits_{p \in \left[ {0,1} \right]} \left\{ {\left| {B_n \left( p \right) - g\left( p \right)} \right|} \right\}}[/latex] i kaže da mu je limes 0)
http://en.wikipedia.org/wiki/Weierstrass_theorem :
In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function.
Umjesto ove općenitije tvrdnje, mi smo pokazali da vrijedi da se funkcija 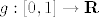 može uniformno aproksimirati nizom Bernsteineovih polinoma, što zapravo znači da niz funkcija može uniformno aproksimirati nizom Bernsteineovih polinoma, što zapravo znači da niz funkcija 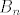 uniformno konvergira prema funkciji uniformno konvergira prema funkciji  , odnosno , odnosno 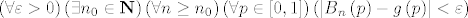 . Ako pogledamo gornji zapis, vidimo da ako smanjujemo . Ako pogledamo gornji zapis, vidimo da ako smanjujemo  , , 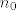 će općenito rasti. će općenito rasti.
Fiksirajmo si neki  i pogledajmo i pogledajmo 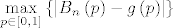 . E sad, definicija uniformne konvergencije niza Bernsteinovih polinoma prema . E sad, definicija uniformne konvergencije niza Bernsteinovih polinoma prema  ti garantira da će se i najveći razmak ti garantira da će se i najveći razmak 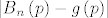 smanjit na manje od smanjit na manje od  nakon nekog nakon nekog  za za 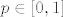 , što možeš napisat i kao , što možeš napisat i kao 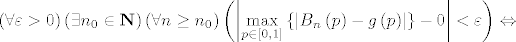 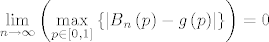 (ovo gore je definicija limesa niza (ovo gore je definicija limesa niza 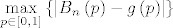 i kaže da mu je limes 0) i kaže da mu je limes 0)
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
|







