| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
MKova
Forumaš(ica)

Pridružen/a: 01. 10. 2005. (18:24:38)
Postovi: (187)16
Spol: 
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
pinkgirl
Forumaš(ica)

Pridružen/a: 30. 11. 2006. (21:08:16)
Postovi: (1AE)16
Spol: 
Lokacija: K-K-Z
|
|
| [Vrh] |
|
pinkgirl
Forumaš(ica)

Pridružen/a: 30. 11. 2006. (21:08:16)
Postovi: (1AE)16
Spol: 
Lokacija: K-K-Z
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
pinkgirl
Forumaš(ica)

Pridružen/a: 30. 11. 2006. (21:08:16)
Postovi: (1AE)16
Spol: 
Lokacija: K-K-Z
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 15:00 sub, 17. 2. 2007 Naslov: Postano: 15:00 sub, 17. 2. 2007 Naslov: |
    |
|
|
Funkcija [latex]f[/latex] je permutacija ako je bijekcija i [latex]f:A \to A[/latex].
Primjer za računanje determinante:
[latex]\det \left[ {\begin{array}{*{20}c}
1 & 3 & 4 \\
2 & 5 & {11} \\
{13} & { - 2} & { - 6} \\
\end{array}} \right][/latex]
(zapis [latex]\sigma = \left( \begin{array}{l}
\begin{array}{*{20}c}
{a_1 } & {a_2 } & {a_3 } \\
\end{array} \\
\begin{array}{*{20}c}
{a_2 } & {a_3 } & {a_1 } \\
\end{array} \\
\end{array} \right)[/latex] znači da je [latex]\sigma \left( {a_1 } \right) = a_2 ,\sigma \left( {a_2 } \right) = a_3 ,\sigma \left( {a_3 } \right) = a_1[/latex])
Promatramo sve permutacije [latex]\sigma :\left\{ {1,2,3} \right\} \to \left\{ {1,2,3} \right\}[/latex]. Ima ih 3! =6 i to su [latex]\sigma _1 = \left( \begin{array}{l}
\begin{array}{*{20}c}
1 & 2 & 3 \\
\end{array} \\
\begin{array}{*{20}c}
1 & 2 & 3 \\
\end{array} \\
\end{array} \right)[/latex], [latex]\sigma _2 = \left( \begin{array}{l}
\begin{array}{*{20}c}
1 & 2 & 3 \\
\end{array} \\
\begin{array}{*{20}c}
1 & 3 & 2 \\
\end{array} \\
\end{array} \right)[/latex], [latex]\sigma _3 = \left( \begin{array}{l}
\begin{array}{*{20}c}
1 & 2 & 3 \\
\end{array} \\
\begin{array}{*{20}c}
2 & 1 & 3 \\
\end{array} \\
\end{array} \right)[/latex], [latex]\sigma _4 = \left( \begin{array}{l}
\begin{array}{*{20}c}
1 & 2 & 3 \\
\end{array} \\
\begin{array}{*{20}c}
2 & 3 & 1 \\
\end{array} \\
\end{array} \right)[/latex], [latex]\sigma _5 = \left( \begin{array}{l}
\begin{array}{*{20}c}
1 & 2 & 3 \\
\end{array} \\
\begin{array}{*{20}c}
3 & 1 & 2 \\
\end{array} \\
\end{array} \right)[/latex] i [latex]\sigma _6 = \left( \begin{array}{l}
\begin{array}{*{20}c}
1 & 2 & 3 \\
\end{array} \\
\begin{array}{*{20}c}
3 & 2 & 1 \\
\end{array} \\
\end{array} \right)[/latex]. Brojevi inverzija su redom [latex]I\left( {\sigma _1 } \right) = 0,I\left( {\sigma _2 } \right) = 1,I\left( {\sigma _3 } \right) = 1,I\left( {\sigma _4 } \right) = 2,I\left( {\sigma _5 } \right) = 2,I\left( {\sigma _6 } \right) = 3[/latex]. Sad imamo:
[latex]\det \left[ {\begin{array}{*{20}c}
1 & 3 & 4 \\
2 & 5 & {11} \\
{13} & { - 2} & { - 6} \\
\end{array}} \right] = \sum\limits_{\sigma \in S_3 } {\left( { - 1} \right)^{I\left( \sigma \right)} \prod\limits_{i = 1}^3 {a_{i,\sigma \left( i \right)} } } =[/latex]
[latex]\left( { - 1} \right)^{I\left( {\sigma _1 } \right)} \prod\limits_{i = 1}^3 {a_{i,\sigma _1 \left( i \right)} } + \left( { - 1} \right)^{I\left( {\sigma _2 } \right)} \prod\limits_{i = 1}^3 {a_{i,\sigma _2 \left( i \right)} } + ... =[/latex]
[latex] = \left( { - 1} \right)^0 a_{11} a_{22} a_{33} + \left( { - 1} \right)^1 a_{11} a_{23} a_{32} + ... =[/latex][latex] = 1 \cdot 5 \cdot \left( { - 6} \right) - 1 \cdot 11 \cdot \left( { - 2} \right) + ...[/latex]
EDIT: evo, hvala na upozorenju, ispravljeno
Funkcija  je permutacija ako je bijekcija i je permutacija ako je bijekcija i 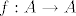 . .
Primjer za računanje determinante:
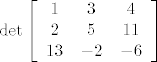
(zapis 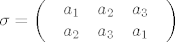 znači da je znači da je 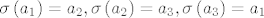 ) )
Promatramo sve permutacije 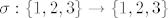 . Ima ih 3! =6 i to su . Ima ih 3! =6 i to su 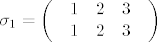 , , 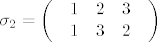 , , 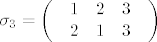 , , 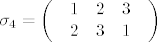 , , 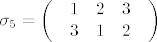 i i 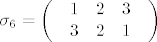 . Brojevi inverzija su redom . Brojevi inverzija su redom 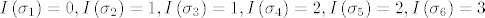 . Sad imamo: . Sad imamo:
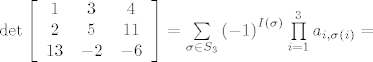
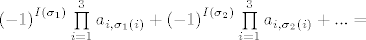
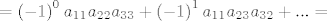 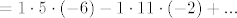
EDIT: evo, hvala na upozorenju, ispravljeno
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
Zadnja promjena: alen; 17:40 sub, 17. 2. 2007; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
ß
Forumaš(ica)
Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
|
| [Vrh] |
|
pinkgirl
Forumaš(ica)

Pridružen/a: 30. 11. 2006. (21:08:16)
Postovi: (1AE)16
Spol: 
Lokacija: K-K-Z
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
|
| [Vrh] |
|
pinkgirl
Forumaš(ica)

Pridružen/a: 30. 11. 2006. (21:08:16)
Postovi: (1AE)16
Spol: 
Lokacija: K-K-Z
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
herman
Forumaš(ica)

Pridružen/a: 07. 11. 2006. (19:51:13)
Postovi: (63)16
|
 Postano: 22:24 ned, 18. 2. 2007 Naslov: Postano: 22:24 ned, 18. 2. 2007 Naslov: |
    |
|
|
[quote="pinkgirl"]...det(A*A^-1)=detI <=> det A!=0 i detA^-1=1/det A
tu?[/quote]
Ne baš tako doslovno. :D
Uglavnom, imaš tvrdnju koju treba dokazati:
Matrica A je regularna <=> detA != 0.
Dokazala si smjer =>. Trebaš dokazati smjer <=, i time si dokazala tvrdnju. Dakle, pretpostavi da je detA != 0, i iskoristi relaciju AA*=(detA)I, pomoću koje ćeš pokazati da A ima inverz, tj. da je regularna. :)
| pinkgirl (napisa): | ...det(A*A^-1)=detI ⇔ det A!=0 i detA^-1=1/det A
tu? |
Ne baš tako doslovno. 
Uglavnom, imaš tvrdnju koju treba dokazati:
Matrica A je regularna ⇔ detA != 0.
Dokazala si smjer ⇒. Trebaš dokazati smjer ⇐, i time si dokazala tvrdnju. Dakle, pretpostavi da je detA != 0, i iskoristi relaciju AA*=(detA)I, pomoću koje ćeš pokazati da A ima inverz, tj. da je regularna. 
|
|
| [Vrh] |
|
pinkgirl
Forumaš(ica)

Pridružen/a: 30. 11. 2006. (21:08:16)
Postovi: (1AE)16
Spol: 
Lokacija: K-K-Z
|
|
| [Vrh] |
|
pinkgirl
Forumaš(ica)

Pridružen/a: 30. 11. 2006. (21:08:16)
Postovi: (1AE)16
Spol: 
Lokacija: K-K-Z
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
 Postano: 22:43 ned, 18. 2. 2007 Naslov: Postano: 22:43 ned, 18. 2. 2007 Naslov: |
    |
|
|
[quote="Mr.Doe"][quote="alen"]Funkcija [latex]f[/latex] je permutacija ako je bijekcija i [latex]f:A \to A[/latex]. [/quote]
Ovo ti bas nema prevelikog smisla ako nije [latex]A\subset \mathbb{N}[/latex].
Bijekcija sa sa [latex]\mathbb{R}\rightarrow \mathbb{R}[/latex] nije permutacija. Ok? :wink:[/quote]
Isprike, treba dodati da je [latex]A[/latex] konačan.
In abstract algebra and related areas, the elements of permutation may not be arranged in a linear order, or indeed in any order at all. Under this refined definition, a permutation is a bijection from a finite set X onto itself.
Dakle [latex]f:\left\{ {\sqrt 2 ,\sqrt 3 } \right\} \to \left\{ {\sqrt 2 ,\sqrt 3 } \right\}[/latex], [latex]f[/latex] bijekcija je također permutacija, iako [latex]\left\{ {\sqrt 2 ,\sqrt 3 } \right\} \not\subset {\bf N}[/latex]. Bijekcija [latex]f:2{\bf N} \to 2{\bf N}[/latex] nije permutacija, iako je [latex]2{\bf N} \subseteq {\bf N}[/latex].
| Mr.Doe (napisa): | | alen (napisa): | Funkcija  je permutacija ako je bijekcija i je permutacija ako je bijekcija i 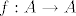 . . |
Ovo ti bas nema prevelikog smisla ako nije 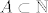 . .
Bijekcija sa sa 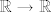 nije permutacija. Ok? nije permutacija. Ok?  |
Isprike, treba dodati da je  konačan. konačan.
In abstract algebra and related areas, the elements of permutation may not be arranged in a linear order, or indeed in any order at all. Under this refined definition, a permutation is a bijection from a finite set X onto itself.
Dakle 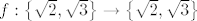 , ,  bijekcija je također permutacija, iako bijekcija je također permutacija, iako 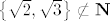 . Bijekcija . Bijekcija 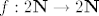 nije permutacija, iako je nije permutacija, iako je  . .
_________________
Između ostalog, mislim da bi kolegij mjera i integral trebao imati svoj podforum među kolegijima treće godine
|
|
| [Vrh] |
|
|

















