| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 13:13 ned, 13. 4. 2008 Naslov: Postano: 13:13 ned, 13. 4. 2008 Naslov: |
    |
|
|
Mora se napraviti (7+1)x(10+1) matrica koju ćeš popunjavati na način
[latex]F(i,j)=\max{ \left\{
\begin{array}{l}
F(i-1,j-1)+B(x_i,y_i),\\
F(i-1,j)-d,\\
F(i,j-1)-d
\end{array}
\right.}[/latex]
uz uvjete d=8, F(0,j)=-j*d, F(i,0)=-i*d. B(x_i,y_i) je score među dvije aminokiseline koji je dan u blosum matrici B napisanoj u kosturu programa na http://web.math.hr/~karaga/nwkostur.c .
Uvodi se još matrica P kojom se pamti iz koje ćelije smo izračunali ćeliju F(i,j). Ako je maksimum u F(i,j) bio F(i-1,j-1)+B(xi,yi), onda P(i,j)=1, to jest došli smo iz ćelije gore-lijevo. Ako je max bio F(i,j-1), onda P(i,j)=2, došli smo slijeva. Ako je max bio F(i-1,j)-d, onda P(i,j)=3, to jest došli smo odozgo. Uvjet na P je P(0,0)=0.
Zadnji element u matrici F će dati najbolji score poravnanja i sada moraš pomoću matrice P otkriti kojim putem se je došlo do tog scorea. Kreće se [u]od kraja[/u] matrice P.
Ako je P(i,j)=1, znači da smo došli od gore lijevo pa u niz xx (to jest string u koji ispisujemo poravnanje za x) upisujemo x_i, a u drugi niz (poravnanje za y) upisujemo y_j i prebacujemo se u element koji je gore-lijevo u matrici P, tj. P(i-1,j-1).
Ako je P(i,j)=2, onda smo došli slijeva i u niz za x ispisujemo '-', a u niz za y ispisujemo y_j i prebacujemo se u P(i,j-1).
Ako je P(i,j)=3, onda smo došli odozgo i u niz za x ispisujemo x_i, a u niz za y ispisujemo '-' i prebacujemo se u P(i-1,j).
To se radi dok P(i,j)!=0, to jest dok se ne dođe do početka matrice P.
Sada se još stringovi u kojima je upisano poravnanje moraju ispisati jedan ispod drugoga, ali u obrnutom redoslijedu jer smo pomoću matrice P poravnanje upisivali odozada.
Upute za algoritam su ispisane u udžbeniku Durbin, Eddy, Krogh, Mitchison - Biological Sequence Analysis.
Na stranici asist. Karage je ispisana matrica F koja se mora dobiti (uz mali ispravak: score između P i W mora biti -41, ne -42) a strelice na toj matrici označuju iz koje ćelije je koji element izračunat. Može se desiti da nekome matrica P bude nešto drugačija nego što je to na "službenoj" matrici jer se može desiti da F(i,j) može imati maksimum i ako dolazi od F(i-1,j-1) i ako dolazi od F(i-1,j) i ako dolazi od F(i,j-1) to jest u element (i,j) se može doći iz više ćelija.
Mora se napraviti (7+1)x(10+1) matrica koju ćeš popunjavati na način
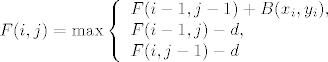
uz uvjete d=8, F(0,j)=-j*d, F(i,0)=-i*d. B(x_i,y_i) je score među dvije aminokiseline koji je dan u blosum matrici B napisanoj u kosturu programa na http://web.math.hr/~karaga/nwkostur.c .
Uvodi se još matrica P kojom se pamti iz koje ćelije smo izračunali ćeliju F(i,j). Ako je maksimum u F(i,j) bio F(i-1,j-1)+B(xi,yi), onda P(i,j)=1, to jest došli smo iz ćelije gore-lijevo. Ako je max bio F(i,j-1), onda P(i,j)=2, došli smo slijeva. Ako je max bio F(i-1,j)-d, onda P(i,j)=3, to jest došli smo odozgo. Uvjet na P je P(0,0)=0.
Zadnji element u matrici F će dati najbolji score poravnanja i sada moraš pomoću matrice P otkriti kojim putem se je došlo do tog scorea. Kreće se od kraja matrice P.
Ako je P(i,j)=1, znači da smo došli od gore lijevo pa u niz xx (to jest string u koji ispisujemo poravnanje za x) upisujemo x_i, a u drugi niz (poravnanje za y) upisujemo y_j i prebacujemo se u element koji je gore-lijevo u matrici P, tj. P(i-1,j-1).
Ako je P(i,j)=2, onda smo došli slijeva i u niz za x ispisujemo '-', a u niz za y ispisujemo y_j i prebacujemo se u P(i,j-1).
Ako je P(i,j)=3, onda smo došli odozgo i u niz za x ispisujemo x_i, a u niz za y ispisujemo '-' i prebacujemo se u P(i-1,j).
To se radi dok P(i,j)!=0, to jest dok se ne dođe do početka matrice P.
Sada se još stringovi u kojima je upisano poravnanje moraju ispisati jedan ispod drugoga, ali u obrnutom redoslijedu jer smo pomoću matrice P poravnanje upisivali odozada.
Upute za algoritam su ispisane u udžbeniku Durbin, Eddy, Krogh, Mitchison - Biological Sequence Analysis.
Na stranici asist. Karage je ispisana matrica F koja se mora dobiti (uz mali ispravak: score između P i W mora biti -41, ne -42) a strelice na toj matrici označuju iz koje ćelije je koji element izračunat. Može se desiti da nekome matrica P bude nešto drugačija nego što je to na "službenoj" matrici jer se može desiti da F(i,j) može imati maksimum i ako dolazi od F(i-1,j-1) i ako dolazi od F(i-1,j) i ako dolazi od F(i,j-1) to jest u element (i,j) se može doći iz više ćelija.
_________________
The Dude Abides
|
|
| [Vrh] |
|
pins
Forumaš(ica)

Pridružen/a: 07. 12. 2006. (16:18:23)
Postovi: (17)16
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
ivanzub
Forumaš(ica)

Pridružen/a: 08. 02. 2006. (11:16:46)
Postovi: (CC)16
|
 Postano: 14:37 čet, 8. 5. 2008 Naslov: Postano: 14:37 čet, 8. 5. 2008 Naslov: |
    |
|
|
[quote="goranm"]
Ako je P(i,j)=2, onda smo došli slijeva i u niz za x ispisujemo '-', a u niz za y ispisujemo y_j i prebacujemo se u P(i,j-1).
Ako je P(i,j)=3, onda smo došli odozgo i u niz za x ispisujemo x_i, a u niz za y ispisujemo '-' i prebacujemo se u P(i-1,j).[/quote]
Gorane, hvala ti na ovome postu. uvelike si mi pomogao pri rjesavanju zadace.
Samo mala ispravka, kada je P=2 -> u niz x ispisujemo x_i, a u niz y '-'
P=3 -> u niz x ide '-' a u niz y ide y_i (prebacivanje ostaje kako pise).
EDIT: ma vrijedi i jedno i drugo, ovisno o tome kako je napravljena matrica F.
| goranm (napisa): |
Ako je P(i,j)=2, onda smo došli slijeva i u niz za x ispisujemo '-', a u niz za y ispisujemo y_j i prebacujemo se u P(i,j-1).
Ako je P(i,j)=3, onda smo došli odozgo i u niz za x ispisujemo x_i, a u niz za y ispisujemo '-' i prebacujemo se u P(i-1,j). |
Gorane, hvala ti na ovome postu. uvelike si mi pomogao pri rjesavanju zadace.
Samo mala ispravka, kada je P=2 → u niz x ispisujemo x_i, a u niz y '-'
P=3 → u niz x ide '-' a u niz y ide y_i (prebacivanje ostaje kako pise).
EDIT: ma vrijedi i jedno i drugo, ovisno o tome kako je napravljena matrica F.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
13_mac
Forumaš(ica)


Pridružen/a: 23. 10. 2006. (22:56:13)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
biba
Forumaš(ica)

Pridružen/a: 07. 11. 2005. (19:53:02)
Postovi: (45)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 12:32 čet, 22. 5. 2008 Naslov: Postano: 12:32 čet, 22. 5. 2008 Naslov: |
    |
|
|
Jel netko rješava Viterbija da mi provjeri matrice M i P?
Napomena: dobro je i ako je transponirana, ja sam uzeo da su stupci slova, a retci stanja
Prilažem i datoteku sa matricama emisija i tranzicija, unutra je i niz
i trebo bih pomoć kod backtrackinga... :beg:
Hvala :D
Jel netko rješava Viterbija da mi provjeri matrice M i P?
Napomena: dobro je i ako je transponirana, ja sam uzeo da su stupci slova, a retci stanja
Prilažem i datoteku sa matricama emisija i tranzicija, unutra je i niz
i trebo bih pomoć kod backtrackinga... 
Hvala 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy 
| Description: |
|

Download |
| Filename: |
vitulaz.txt |
| Filesize: |
915 Bytes |
| Downloaded: |
334 Time(s) |
| Description: |
|

Download |
| Filename: |
datoteka.txt |
| Filesize: |
714 Bytes |
| Downloaded: |
332 Time(s) |
|
|
| [Vrh] |
|
bubble
Forumaš(ica)


Pridružen/a: 14. 02. 2007. (00:21:29)
Postovi: (8C)16
Spol: 
|
 Postano: 16:18 čet, 22. 5. 2008 Naslov: Postano: 16:18 čet, 22. 5. 2008 Naslov: |
    |
|
|
Meni su stanja stupci, redovi slova niza. Evo sto sam ja dobila (i jos neki, pa se nadam da je dobro, ali ako je jos netko dobio.. :))
MATRICA M
1.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
0.000000 0.000000 0.040000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
0.000000 0.000000 0.000000 0.000180 0.001700 0.000000 0.000000 0.000000 0.000000
0.000000 0.000000 0.000000 0.000019 0.000002 0.000013 0.000101 0.000000 0.000000
0.000000 0.000000 0.000000 0.000000 0.000000 0.000001 0.000000 0.000004 0.000004
MATRICA P
-1 -1 -1 -1 -1 -1 -1 -1 -1
-1 0 0 3 3 5 5 7 7
-1 1 1 2 2 5 5 7 7
-1 1 1 3 3 4 4 7 7
-1 1 1 3 3 5 5 6 7
Konacno rjesenje: B-M1-M2-M3-I3-E
Luuka, rado bi ti pomogla ali ne zelim ti krivo nesto reci. Ako je netko ovo dobio (ili nije), molim ga da bude dobar i napise sto je dobio. :)
Ne da mi se pisat ni nacin na koji sam dobila P ako ovo konacno ne valja.. ah..
Meni su stanja stupci, redovi slova niza. Evo sto sam ja dobila (i jos neki, pa se nadam da je dobro, ali ako je jos netko dobio..  ) )
MATRICA M
1.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
0.000000 0.000000 0.040000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
0.000000 0.000000 0.000000 0.000180 0.001700 0.000000 0.000000 0.000000 0.000000
0.000000 0.000000 0.000000 0.000019 0.000002 0.000013 0.000101 0.000000 0.000000
0.000000 0.000000 0.000000 0.000000 0.000000 0.000001 0.000000 0.000004 0.000004
MATRICA P
-1 -1 -1 -1 -1 -1 -1 -1 -1
-1 0 0 3 3 5 5 7 7
-1 1 1 2 2 5 5 7 7
-1 1 1 3 3 4 4 7 7
-1 1 1 3 3 5 5 6 7
Konacno rjesenje: B-M1-M2-M3-I3-E
Luuka, rado bi ti pomogla ali ne zelim ti krivo nesto reci. Ako je netko ovo dobio (ili nije), molim ga da bude dobar i napise sto je dobio. 
Ne da mi se pisat ni nacin na koji sam dobila P ako ovo konacno ne valja.. ah..
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 16:32 čet, 22. 5. 2008 Naslov: Postano: 16:32 čet, 22. 5. 2008 Naslov: |
    |
|
|
Za NADV rješenje je B-M1-M2-I2-M3-E. Tako reko profesor...
Za NADV rješenje je B-M1-M2-I2-M3-E. Tako reko profesor...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
bubble
Forumaš(ica)


Pridružen/a: 14. 02. 2007. (00:21:29)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
|




















