| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
zzsan
Forumaš(ica)

Pridružen/a: 25. 11. 2005. (20:53:14)
Postovi: (89)16
|
|
| [Vrh] |
|
m00nblade
Forumaš(ica)

Pridružen/a: 30. 10. 2005. (13:26:10)
Postovi: (54)16
Spol: 
|
|
| [Vrh] |
|
zzsan
Forumaš(ica)

Pridružen/a: 25. 11. 2005. (20:53:14)
Postovi: (89)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
FFF
Forumaš(ica)


Pridružen/a: 19. 11. 2006. (19:46:12)
Postovi: (2A)16
|
|
| [Vrh] |
|
zzsan
Forumaš(ica)

Pridružen/a: 25. 11. 2005. (20:53:14)
Postovi: (89)16
|
|
| [Vrh] |
|
FFF
Forumaš(ica)


Pridružen/a: 19. 11. 2006. (19:46:12)
Postovi: (2A)16
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
 Postano: 3:11 sri, 18. 4. 2007 Naslov: Postano: 3:11 sri, 18. 4. 2007 Naslov: |
    |
|
|
Zadatak ipak nije tako jednostavan.
Do visine 4 paraboloid se nalazi unutar elipse ako gledamo u xy ravnini, a od 4 do 9 izlazi iz njega ali samo na jednoj poluosi (y-osi)(jer paraboloid opisuje kruznice na nekoj konstantnoj visini z)
Ako mozes zamislit, recimo da stojis na vrhu tijela i sad se vozis krenes iz (3,0,9) i ides po elipsi past ces u rupu tj u tocku (0,2,4) ionda se opet dizes do (-3,0,9) i zavrsavas u dolini u (0,-2,4), kuzis nije jednake visine tijelo. Potrebno ga je izintegrirat do visine 4 ovak kak si ti cini mi se a onda je problematicno (u presjeku imas 2 polumjeseca koji su sve manji i manji jer se upisuju sve vece kruznice)
Ako ce bit uistinu 4+4 tako kompliciran zadatak ne bi trebao bit
Zadatak ipak nije tako jednostavan.
Do visine 4 paraboloid se nalazi unutar elipse ako gledamo u xy ravnini, a od 4 do 9 izlazi iz njega ali samo na jednoj poluosi (y-osi)(jer paraboloid opisuje kruznice na nekoj konstantnoj visini z)
Ako mozes zamislit, recimo da stojis na vrhu tijela i sad se vozis krenes iz (3,0,9) i ides po elipsi past ces u rupu tj u tocku (0,2,4) ionda se opet dizes do (-3,0,9) i zavrsavas u dolini u (0,-2,4), kuzis nije jednake visine tijelo. Potrebno ga je izintegrirat do visine 4 ovak kak si ti cini mi se a onda je problematicno (u presjeku imas 2 polumjeseca koji su sve manji i manji jer se upisuju sve vece kruznice)
Ako ce bit uistinu 4+4 tako kompliciran zadatak ne bi trebao bit
_________________ Kad sam bila mala htjela sam biti statističarka 
[tex]\omega \in \Omega[/tex] 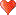 |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
marijap
Forumaš(ica)


Pridružen/a: 21. 06. 2006. (19:04:40)
Postovi: (209)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
|








