| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 17:32 čet, 28. 6. 2007 Naslov: Postano: 17:32 čet, 28. 6. 2007 Naslov: |
    |
|
|
Mozemo to zakljuciti.
Dokaz cak nije tako tezak. Napisat cu ti ga tu ako treba, ali daj probaj prvo sam. Moj savjet bi ti bio da dokazujes na ovom tvom apstraktnom: dakle, A izom B, C i D podgpe od A i B, i C normalna u A. Tvrdnja je D normalna u B. Jos ce ti trebat da nekak nazoves taj izomorfizam, npr. f sa A u B je izomorfizam a f na minus prvu njegov inverz sa B u A.
Mozemo to zakljuciti.
Dokaz cak nije tako tezak. Napisat cu ti ga tu ako treba, ali daj probaj prvo sam. Moj savjet bi ti bio da dokazujes na ovom tvom apstraktnom: dakle, A izom B, C i D podgpe od A i B, i C normalna u A. Tvrdnja je D normalna u B. Jos ce ti trebat da nekak nazoves taj izomorfizam, npr. f sa A u B je izomorfizam a f na minus prvu njegov inverz sa B u A.
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 1:07 pet, 29. 6. 2007 Naslov: Postano: 1:07 pet, 29. 6. 2007 Naslov: |
    |
|
|
Ne, sori, totalno sam zabrijala. Upravo me Tantun upozorio u pm-u da sam se zaletila.
Tvrdnja ne vrijedi.
On veli ovo:
[quote="Tantun"]Promatraj [latex]A=B=\mathbb{Z}_{2} \oplus S_{n}[/latex], za [latex]n \geq 3[/latex]. Podgrupe [latex]C=\mathbb{Z}_{2} \times \left\{id\right\}[/latex] i [latex]D=\left\{(0,id),(0,\tau)\right\}[/latex], gdje je [latex]\tau[/latex] proizvoljna tranzpozicija, su izomorfne (obje su izomorfne sa [latex]\mathbb{Z}_{2}[/latex]), [latex]C[/latex] je normalna, [latex]D[/latex] nije.
Uoci i da je [latex]\mathbb{Z}_{2} \oplus S_{n}[/latex] izomorfno s [latex]D \oplus S_{n}[/latex] (jer je [latex]D[/latex] izomorfno s [latex]\mathbb{Z}_{2}[/latex]). Dakle ove dvije podgrupe ([latex]D[/latex] i [latex]S_{n}[/latex] s prirodnim ulaganjem) od [latex]\mathbb{Z}_{2} \oplus S_{n}[/latex] zadovoljavaju uvjete teorema. No [latex]D[/latex] ne zadovoljava (1) u iskazu teorema. Stovise ni (2) ni (3) ne vrijede.[/quote]
Ne, sori, totalno sam zabrijala. Upravo me Tantun upozorio u pm-u da sam se zaletila.
Tvrdnja ne vrijedi.
On veli ovo:
| Tantun (napisa): | Promatraj 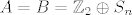 , za , za 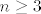 . Podgrupe . Podgrupe 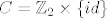 i i 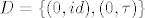 , gdje je , gdje je  proizvoljna tranzpozicija, su izomorfne (obje su izomorfne sa proizvoljna tranzpozicija, su izomorfne (obje su izomorfne sa 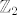 ), ),  je normalna, je normalna, 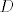 nije. nije.
Uoci i da je  izomorfno s izomorfno s 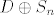 (jer je (jer je 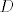 izomorfno s izomorfno s 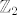 ). Dakle ove dvije podgrupe ( ). Dakle ove dvije podgrupe (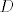 i i 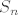 s prirodnim ulaganjem) od s prirodnim ulaganjem) od  zadovoljavaju uvjete teorema. No zadovoljavaju uvjete teorema. No 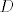 ne zadovoljava (1) u iskazu teorema. Stovise ni (2) ni (3) ne vrijede. ne zadovoljava (1) u iskazu teorema. Stovise ni (2) ni (3) ne vrijede. |
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
 Postano: 11:20 pet, 29. 6. 2007 Naslov: Postano: 11:20 pet, 29. 6. 2007 Naslov: |
    |
|
|
Da ne ucim taj teorem jer je kriv? Ili ga treba nekako zakrpat
pa npr. umjesto da se kaze G izomorfno s direktnom sumom Gi -eva ako i samo ako 1,2,3. da kazemo funkcija phi: koja ide s direktne sume Gi-eva u G tako sto pomnozi sve kordinate je izomorfizam ako i samo ako 1,2,3? Tako je dokaz zakrpan, ne?
Da ne ucim taj teorem jer je kriv? Ili ga treba nekako zakrpat
pa npr. umjesto da se kaze G izomorfno s direktnom sumom Gi -eva ako i samo ako 1,2,3. da kazemo funkcija phi: koja ide s direktne sume Gi-eva u G tako sto pomnozi sve kordinate je izomorfizam ako i samo ako 1,2,3? Tako je dokaz zakrpan, ne?
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 13:55 pet, 29. 6. 2007 Naslov: Postano: 13:55 pet, 29. 6. 2007 Naslov: |
    |
|
|
Da, tako je dokaz zakrpan.
Hoces ti ic upozorit prof. Sirolu, kao legitimni vlasnik autorskog prava na pronadenu gresku, ili da idem ja pravit se pamenta na tudi racun? :)
I sori kaj sam ti gore davala onaj trivijani savjet, malo sam se navikla na jednu odredenu razinu znanja koja je otuzna :oops:
Da, tako je dokaz zakrpan.
Hoces ti ic upozorit prof. Sirolu, kao legitimni vlasnik autorskog prava na pronadenu gresku, ili da idem ja pravit se pamenta na tudi racun? 
I sori kaj sam ti gore davala onaj trivijani savjet, malo sam se navikla na jednu odredenu razinu znanja koja je otuzna 
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
Braslav
Forumaš(ica)

Pridružen/a: 18. 10. 2005. (19:47:44)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
|








