| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pefri
Forumaš(ica)

Pridružen/a: 09. 02. 2005. (22:34:29)
Postovi: (20)16
|
|
| [Vrh] |
|
pefri
Forumaš(ica)

Pridružen/a: 09. 02. 2005. (22:34:29)
Postovi: (20)16
|
 Postano: 18:13 pet, 31. 8. 2007 Naslov: Postano: 18:13 pet, 31. 8. 2007 Naslov: |
    |
|
|
e i jos nešto zadatak ide:
Odredite sve potprostore vekt.pr.R^2 uz standardne operacije zbrajanja vektora i množenja vektora skalarom.
Rj.
[b]To su prazan skup, R^2 , A= {(0,y): ye R}, B= {(x,0): xe R}, C={(x,tx): xeR, teR} [/b]
Ima li jos koji?
e i jos nešto zadatak ide:
Odredite sve potprostore vekt.pr.R^2 uz standardne operacije zbrajanja vektora i množenja vektora skalarom.
Rj.
To su prazan skup, R^2 , A= {(0,y): ye R}, B= {(x,0): xe R}, C={(x,tx): xeR, teR}
Ima li jos koji?
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
 Postano: 21:57 pet, 31. 8. 2007 Naslov: Postano: 21:57 pet, 31. 8. 2007 Naslov: |
    |
|
|
[quote="pefri"]
Rj.
[b]To su prazan skup, R^2 , A= {(0,y): ye R}, B= {(x,0): xe R}, C={(x,tx): xeR, teR} [/b]
Ima li jos koji?[/quote]
nema, samo bih dodao da nije prazan skup vec skup {(0,0)}, da je C citava familija potprostora [latex](C_t)_{t\in \mathbb{R}}[/latex], [latex]C_t=\{(x,tx): x\in \mathbb{R}\}[/latex], gdje je jos B=C_0.
uglavnom, trivijalan, citav prostor i svi pravci kroz ishodiste.
[color=blue][b]Moderator:[/b] Malo izmijenjen LaTeX kod: [tt]{...}[/tt] je grupiranje elemenata; ako želite napisati skup, onda se to radi s [/color][tt][color=red]\[/color][color=blue]{...[/color][color=red]\[/color][color=blue]}[/tt].[/color]
| pefri (napisa): |
Rj.
To su prazan skup, R^2 , A= {(0,y): ye R}, B= {(x,0): xe R}, C={(x,tx): xeR, teR}
Ima li jos koji? |
nema, samo bih dodao da nije prazan skup vec skup {(0,0)}, da je C citava familija potprostora 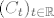 , , 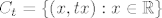 , gdje je jos B=C_0. , gdje je jos B=C_0.
uglavnom, trivijalan, citav prostor i svi pravci kroz ishodiste.
Moderator: Malo izmijenjen LaTeX kod: {...} je grupiranje elemenata; ako želite napisati skup, onda se to radi s \{...\}.
_________________  |
|
| [Vrh] |
|
pefri
Forumaš(ica)

Pridružen/a: 09. 02. 2005. (22:34:29)
Postovi: (20)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
 Postano: 19:59 pon, 24. 9. 2007 Naslov: Postano: 19:59 pon, 24. 9. 2007 Naslov: |
    |
|
|
imas li vjezbe? cini mi se da su oba zadatka rijesena tamo.
hintovi za prvi: sto znas o spektru hermitskog operatora? jesi li vidio lemu koja govori nesto o konveksnoj ljusci spektra?
za drugi zadatak:
a) => b). oznaci onaj zatvoreni potprostor iz uvjeta sa A_m. tada a_m nije element od A_m, te postoji ortogonalni komplement od A_m koji oznacimo sa B_m. Znas da je H direktna suma od A_m i B_m. Sada a_m=x_m + y_m gdje je x_m iz A_m, a y_m iz B_m. (ovo sve radimo jer pokusavmo konstruirati element koji je okomit na sve a_n za n razlicito od m).
pogledaj y_m, on je razlicit od 0 jer a_m nije iz A_m. vrijedi (y_m|a_n)=0 za n<>m, a (y_m|a_m)=(y_m|x_m+y_m)=(y_m|x_m)+(y_m|y_m)=||y_m||^2. ako definiras b_m=y_m/||y_m||^2, onda ce biti zadovoljen uvjet b).
b) => a) pretpostavimo da b) vrijedi, ali a) ne vrijedi. svaki element a iz A_m je limes niza x_k u [{a_n; n<>m}] (elementi tog potprostora su konacne linearne kombinacije tih a_n-ova). svaki taj x_k je okomit na b_m, pa je zbog neprekidnosti skalarnog produkta i (a|b_m)=(lim x_k|b_m)=lim (x_k|b_m)=0. No ako a_m je element od A_m onda je (a_m|b_m)=0, sto je kontradikcija s uvjetom b). dakle, b) povlaci a).
imas li vjezbe? cini mi se da su oba zadatka rijesena tamo.
hintovi za prvi: sto znas o spektru hermitskog operatora? jesi li vidio lemu koja govori nesto o konveksnoj ljusci spektra?
za drugi zadatak:
a) ⇒ b). oznaci onaj zatvoreni potprostor iz uvjeta sa A_m. tada a_m nije element od A_m, te postoji ortogonalni komplement od A_m koji oznacimo sa B_m. Znas da je H direktna suma od A_m i B_m. Sada a_m=x_m + y_m gdje je x_m iz A_m, a y_m iz B_m. (ovo sve radimo jer pokusavmo konstruirati element koji je okomit na sve a_n za n razlicito od m).
pogledaj y_m, on je razlicit od 0 jer a_m nije iz A_m. vrijedi (y_m|a_n)=0 za n<>m, a (y_m|a_m)=(y_m|x_m+y_m)=(y_m|x_m)+(y_m|y_m)=||y_m||^2. ako definiras b_m=y_m/||y_m||^2, onda ce biti zadovoljen uvjet b).
b) ⇒ a) pretpostavimo da b) vrijedi, ali a) ne vrijedi. svaki element a iz A_m je limes niza x_k u [{a_n; n<>m}] (elementi tog potprostora su konacne linearne kombinacije tih a_n-ova). svaki taj x_k je okomit na b_m, pa je zbog neprekidnosti skalarnog produkta i (a|b_m)=(lim x_k|b_m)=lim (x_k|b_m)=0. No ako a_m je element od A_m onda je (a_m|b_m)=0, sto je kontradikcija s uvjetom b). dakle, b) povlaci a).
_________________  |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
|







