| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 19:04 pet, 24. 2. 2006 Naslov: neprekidnost Postano: 19:04 pet, 24. 2. 2006 Naslov: neprekidnost |
    |
|
|
pomoć??
Neka je dana funkcija f:K((2,1),3)->R sa
f(x,y)={ x^2 , za (x,y)iz Q^2 presjek K((2,1),3)
sqrt(4+4x+2y-x^2-y^2) + x^2, inače }
Odredite točke u kojima je dana fja neprekidna. proširite fju po neprekidnosti.[/url]
pomoć??
Neka je dana funkcija f:K((2,1),3)->R sa
f(x,y)={ x^2 , za (x,y)iz Q^2 presjek K((2,1),3)
sqrt(4+4x+2y-x^2-y^2) + x^2, inače }
Odredite točke u kojima je dana fja neprekidna. proširite fju po neprekidnosti.[/url]
|
|
| [Vrh] |
|
pecina
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (14:15:23)
Postovi: (157)16
Spol: 
Lokacija: Happily traveling through space since 1986!
|
 Postano: 19:25 pet, 24. 2. 2006 Naslov: Postano: 19:25 pet, 24. 2. 2006 Naslov: |
    |
|
|
To je sa zadnjeg pismenog. Vrlo jednostavno.
Neprekidna je u [latex]S=\{(x,y):\sqrt{9 - (x-2)^2-(y-1)^2}\}[/latex], dakle kružnici sa središtem u [latex](2,1)[/latex] radijusa [latex]3[/latex] i vrijedi [latex]f(x,y)=x^2, (x,y) iz S)[/latex]. Ima prekid svagdje unutra.
Proširiš po neprekidnosti van kruga (jer je na rubu neprekidna a unutra ima prekid) tako da [latex]f(x,y)=x^2[/latex] svagdje.
P.S. Moram ici jesti, ali mogu detaljnije kasnije (ovo konkretno za [latex]\epsilon[/latex]) :P
To je sa zadnjeg pismenog. Vrlo jednostavno.
Neprekidna je u 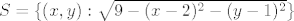 , dakle kružnici sa središtem u , dakle kružnici sa središtem u 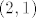 radijusa radijusa 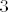 i vrijedi i vrijedi 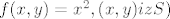 . Ima prekid svagdje unutra. . Ima prekid svagdje unutra.
Proširiš po neprekidnosti van kruga (jer je na rubu neprekidna a unutra ima prekid) tako da 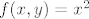 svagdje. svagdje.
P.S. Moram ici jesti, ali mogu detaljnije kasnije (ovo konkretno za  ) ) 
_________________
-- space available for rent --
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
luce
Forumaš(ica)


Pridružen/a: 08. 02. 2006. (19:47:22)
Postovi: (5A)16
Spol: 
|
 Postano: 18:51 sub, 25. 2. 2006 Naslov: Postano: 18:51 sub, 25. 2. 2006 Naslov: |
    |
|
|
Stvar je u tome sta je funkcija neprekidna samo tamo di se ove dvije
'podfunkcije' (ili kako se god to zove :) ) poklapaju.Odnosno di je
x^2 = sqrt(4+4x+2y-x^2-y^2) + x^2
Tocke koje to zadovoljavaju cine neki skup, npr. A. Sada, ako tocka nije u A, onda u njenoj okolini postoje tocke koje su i u Q^2 presjek K((2,1),3) i u 'inace' (jer je Q gust), pa kad gledas limes, on ne ide u 0, pa fja nije neprekidna.
To je malo slobodno objasnjenje :)
Stvar je u tome sta je funkcija neprekidna samo tamo di se ove dvije
'podfunkcije' (ili kako se god to zove  ) poklapaju.Odnosno di je ) poklapaju.Odnosno di je
x^2 = sqrt(4+4x+2y-x^2-y^2) + x^2
Tocke koje to zadovoljavaju cine neki skup, npr. A. Sada, ako tocka nije u A, onda u njenoj okolini postoje tocke koje su i u Q^2 presjek K((2,1),3) i u 'inace' (jer je Q gust), pa kad gledas limes, on ne ide u 0, pa fja nije neprekidna.
To je malo slobodno objasnjenje 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
luce
Forumaš(ica)


Pridružen/a: 08. 02. 2006. (19:47:22)
Postovi: (5A)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pecina
Forumaš(ica)

Pridružen/a: 19. 01. 2005. (14:15:23)
Postovi: (157)16
Spol: 
Lokacija: Happily traveling through space since 1986!
|
 Postano: 12:53 pon, 27. 2. 2006 Naslov: Postano: 12:53 pon, 27. 2. 2006 Naslov: |
    |
|
|
Za neprekidnost na kružnici, uzmeš proizvoljnu točku (na kružnici).
[b](1)[/b] Neka je [latex]T_0=(x_0,y_0,), T \in \ S((2,1),3) \cap QxQ[/latex].
Sada je očito [latex]f(T_0)=x_0^2[/latex]. Sada je lako pokazati da je [latex]\lim_{T \rightarrow T_0}\|f(T)-f(T_0)\| = 0[/latex].
[b](2)[/b] Neka je [latex]T_0=(x_0,y_0,), T \notin \ S((2,1),3) \cap QxQ[/latex].
Sada je očito [latex]f(T_0)=\sqrt{0} + x_0^2[/latex]. I sad isto tako [latex]\lim_{T \rightarrow T_0}\|f(T)-f(T_0)\| = 0[/latex]
Za prekid unutar kruga:
[b](1)[/b] Za [latex]T_0=(x_0,y_0,), T \in \ K((2,1),3) \cap QxQ[/latex] uzeti [latex]\epsilon= \frac{\sqrt{9-(x-2)^2-(y-1)^2}}{2}[/latex]. Mi sad sigurno možemo naći u [latex]\forall \delta > 0[/latex] okolici točke točku [latex]T_\delta=(x_\delta, y_\delta)[/latex] takvu da je [latex]\|f(T_\delta) - f(T)\| > \epsilon[/latex].
Ovo sad nisam tocno siguran kako tocno funkcionira ali bitno ti je naci da je oscilacija u točki [latex]o(T_0) \neq 0[/latex] što je trivijalno (i samo po sebi očito) a povlači da funkcija nije neprekidna. 8)
EDIT: Promijenjeno K u S
Za neprekidnost na kružnici, uzmeš proizvoljnu točku (na kružnici).
(1) Neka je 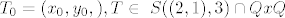 . .
Sada je očito 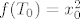 . Sada je lako pokazati da je . Sada je lako pokazati da je 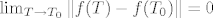 . .
(2) Neka je 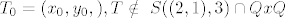 . .
Sada je očito 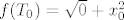 . I sad isto tako . I sad isto tako 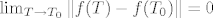
Za prekid unutar kruga:
(1) Za 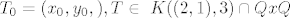 uzeti uzeti 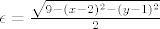 . Mi sad sigurno možemo naći u . Mi sad sigurno možemo naći u 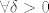 okolici točke točku okolici točke točku 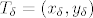 takvu da je takvu da je 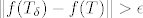 . .
Ovo sad nisam tocno siguran kako tocno funkcionira ali bitno ti je naci da je oscilacija u točki 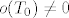 što je trivijalno (i samo po sebi očito) a povlači da funkcija nije neprekidna. što je trivijalno (i samo po sebi očito) a povlači da funkcija nije neprekidna. 
EDIT: Promijenjeno K u S
_________________
-- space available for rent --
Zadnja promjena: pecina; 8:04 pon, 24. 4. 2006; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
davi
Forumaš(ica)

Pridružen/a: 19. 02. 2004. (11:21:27)
Postovi: (36)16
Spol: 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
davi
Forumaš(ica)

Pridružen/a: 19. 02. 2004. (11:21:27)
Postovi: (36)16
Spol: 
|
|
| [Vrh] |
|
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
 Postano: 16:21 čet, 21. 6. 2007 Naslov: Postano: 16:21 čet, 21. 6. 2007 Naslov: |
    |
|
|
Dana je funkcija f:R^2-->R,
f(x,y)={x, x^2EQ ili y^2EQ
{y, inace.
moze li mi netko objasniti gdje trazim nprekidnost,zbunjuju me to kad je x^2EQ.
Ima jos jedan isti takav zadatak,samo sto su malo uvijeti drukciji,funkcija je jednaka x,ako je x-y E Q!
ako mi moze netko moze malo pomoci u vezi ovih uvijeta,tj.gdje da trazim neprekodnost.
Hvala
Dana je funkcija f:R^2-->R,
f(x,y)={x, x^2EQ ili y^2EQ
{y, inace.
moze li mi netko objasniti gdje trazim nprekidnost,zbunjuju me to kad je x^2EQ.
Ima jos jedan isti takav zadatak,samo sto su malo uvijeti drukciji,funkcija je jednaka x,ako je x-y E Q!
ako mi moze netko moze malo pomoci u vezi ovih uvijeta,tj.gdje da trazim neprekodnost.
Hvala
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 17:45 čet, 21. 6. 2007 Naslov: Postano: 17:45 čet, 21. 6. 2007 Naslov: |
    |
|
|
Napisah naopacke, pa da sada ne mijenjam cijeli post, gledam za tocku [latex](e, \pi)[/latex]... :)
Uzmi [latex]\epsilon = 10^{-n}[/latex] za neki [i]n[/i], te [latex]\pi_n[/latex] broj [latex]\pi[/latex] zapisan do [i]n[/i]-te decimale. :-s Recimo, za [i]n[/i] = 2 je [latex]\pi_n=3.14[/latex] i [latex]\epsilon = 10^{-2} = 0.01[/latex] Ocito je:
[latex]0<\pi-\pi_n < \epsilon[/latex].
No, takodjer je i [latex]\pi_n \in \mathbb{Q}[/latex] za svaki [i]n[/i]. :) Sada uvrsti to sto znas u onu formulu gore, sjeti se da neprekidna funkcija preslikava konvergentni niz u niz koji konvergira ka f(x) (gdje je x ono cemu konvergira originalni niz) i primijeti da je
[latex](e, \pi_n) \rightarrow (e, \pi),\quad n \rightarrow \infty[/latex], ali
[latex]f(e, \pi_n) = e\ \forall n \Rightarrow f(e, \pi_n) \rightarrow e,\quad n \rightarrow \infty[/latex]
No,
[latex]f(e, \pi) = \pi[/latex]
Slicno je i kod drugih takvih zadataka. 8)
Napisah naopacke, pa da sada ne mijenjam cijeli post, gledam za tocku 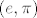 ... ... 
Uzmi 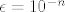 za neki n, te za neki n, te 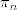 broj broj  zapisan do n-te decimale. zapisan do n-te decimale.  Recimo, za n = 2 je Recimo, za n = 2 je 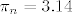 i i 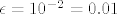 Ocito je: Ocito je:
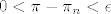 . .
No, takodjer je i 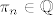 za svaki n. za svaki n.  Sada uvrsti to sto znas u onu formulu gore, sjeti se da neprekidna funkcija preslikava konvergentni niz u niz koji konvergira ka f(x) (gdje je x ono cemu konvergira originalni niz) i primijeti da je Sada uvrsti to sto znas u onu formulu gore, sjeti se da neprekidna funkcija preslikava konvergentni niz u niz koji konvergira ka f(x) (gdje je x ono cemu konvergira originalni niz) i primijeti da je
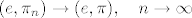 , ali , ali
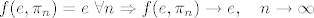
No,
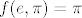
Slicno je i kod drugih takvih zadataka. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
|
| [Vrh] |
|
Tiho
Forumaš(ica)

Pridružen/a: 30. 01. 2006. (17:04:25)
Postovi: (3E)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
|














