Dokaz dovoljnosti: Pretpostavimo suprotno: C nije kompaktan, dakle nije omeđen. Stoga postoji niz (x_k) u C takav da |x_k| neograničeno raste (|.| je norma na R^n). Normiranjem tog niza dolazimo do niza (v_k):
[latex] v_k={{x_k}\over{|x_k|}}[/latex]
koji leži na jediničnoj sferi. Kako je sfera kompaktan skup, taj niz ima konvergentan podniz [latex] v_{k_n} [/latex] s limesom v norme 1 (dakle v nije nulvektor). Tvrdimo da v pripada recesivnom konusu [latex] C_\infty [/latex]
(što daje kontradikciju). Zaista, za proizvoljne x iz C i t>0 vrijedi
[latex] x+tv=\lim_n\left[\left(1-{t\over{|x_{k_n}|}}\right)x+{t\over|x_{k_n}|}x_{k_n}\right][/latex]
Zbog konveksnosti skupa C, niz s desne strane (u uglatoj zagradi) pripada skupu C, pa je zbog zatvorenosti skupa C i njegov limes x+tv također u C.
Dokaz dovoljnosti: Pretpostavimo suprotno: C nije kompaktan, dakle nije omeđen. Stoga postoji niz (x_k) u C takav da |x_k| neograničeno raste (|.| je norma na R^n). Normiranjem tog niza dolazimo do niza (v_k):
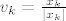
koji leži na jediničnoj sferi. Kako je sfera kompaktan skup, taj niz ima konvergentan podniz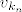 
s limesom v norme 1 (dakle v nije nulvektor). Tvrdimo da v pripada recesivnom konusu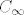 
(što daje kontradikciju). Zaista, za proizvoljne x iz C i t>0 vrijedi
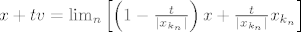
Zbog konveksnosti skupa C, niz s desne strane (u uglatoj zagradi) pripada skupu C, pa je zbog zatvorenosti skupa C i njegov limes x+tv također u C.
_________________
Marko Vrdoljak
