Pitanja vezana uz gradivo

[Mr.Doe]

Evo prvo pitanje :

kako da prevedemo ; balanced incomplete block design ? (gubim se na ovom,balanced)

[krcko]

Moze balansirani, ili hrvatskije uravnotezeni (nepotpuni blok dizajn). Neki kazu blokovni nacrt ili blokovna shema.

_________________
Vedran Krcadinac

Ljudi su razliciti, a nula je paran broj.

[menschen]

Kod algoritma za neadaptivo testiranje...
Mi tražimo podskup pozitivnih elemenata U, al šta nam taj U zapravo predstavlja, tj. šta to točno tražimo?
Malo me buni...

[Gost]

Taj skup U je skup onih ("pozitivnih") elemenata koje želimo identificirati, tj. skup onih elemenata ("uzoraka" ili slično) koji imaju neko određeno svojstvo. Testiraju se, u cjelini, određene skupine uzoraka, "grupe", koje su pozitivne čim je barem jedan element pozitivan. Dakle, treba pogodnim izborom grupa uzoraka minimizirati potreban broj testiranja (cijelih grupa) kako bi se identificirali (svi) pojedini pozitivni elementi. Cilj je da se U jednoznačno rekonstruira iz svog "vektora", tj vrijednosti 0 ili 1 prema tome je li presjek U s pojedinom grupom prazan ili neprazan.
Jednostavnije: znajući sastav pojedinih grupa i podatak je li test pojedine grupe dao pozitivan ili negativan rezultat, želimo identificirati skup svih "pozitivnih" elemenata.

[menschen]

Hvala, kužim sad!!

[Glupko_3.14]

evo, otvorit cu sezonu glupih pitanja i na ovom kolegiju.
savjetovala bih onima koji slucajno nabasu na ovaj post da prate daljnji razvoj topica jer ce vrlo vjerojatno bit nepresusan izvor zabave narednih 36 sati
ujedno se zelim opravdat jeftinim izgovorom da vrlo malo spavam u zadnje vrijeme.

u definiciji blok dizajna v>k stoji zato sto nas nije briga za blok dizajn koji ima jedan blok u kojem su sve tocke, ili ima nesto dublje?

_________________
Nov, još gluplji.

[krcko]

Nema nista dublje. Isto tako nas nije briga za dizajne s k=1 (jer skoro pa ne postoje) i k=2 (jer su to potpuni grafovi).

PS. Pazi da ti vsego ne skuzi dupli account

PPS. Nauci Fisherovu nejednakost

_________________
Vedran Krcadinac

Ljudi su razliciti, a nula je paran broj.

[Glupko_3.14]

[krcko]

Hmmm, a hoce sutra na usmeni doci Ignavija ili Glupko?

Mislim, ak se pojavi Ignavija nju nebum pital Fisherovu nejednakost... to je bil hint za Glupka...

_________________
Vedran Krcadinac

Ljudi su razliciti, a nula je paran broj.

[Glupko_3.14]

[Glupko_3.14]

u dokazu Leme 5.6. u knjizi (afina ravnina reda n zadovoljava euklidov 5. postulat, str. 105) pise da , hmm...
imamo tocku x i blok L={a_1,...,a_n} koji ne sadrzi x
onda za svaki a_i mozemo naci jedinstveni (jer lambda=1) blok L_i koji sadrzi i a_i i x
tamo pise da je u presjeku L_i i L samo a_i. zasto?

p.s. inace (mislim) da razumijem dokaz, i cini mi se da kad bi i bilo recimo neki jos a_j u presjeku (iako je to valjda nemoguce), opet bi nasli M disjunktan s L na isti nacin

p.p.s. u biljeznici mi pod dokazom pise samo r=n+1, b=n^2+n i taj dokaz nisam bas shvatila.

_________________
Nov, još gluplji.

[Ignavia]

cuj Glupko_3.14, daj malo razmisli, pa stvarno si glup

kad bi L_i presjek L sadrzavao dvije tocke, onda bi za taj par tocaka mogli naci dva bloka koja ih sadrze, sto je kontradikcija sa lambda jednako 1

dobro, za ovaj dokaz u biljeznici ti ne mogu trenutno pomoc. ali samo zato sto nemam vremena

_________________
moj prostor

[Glupko_3.14]

u dokazu tm. pod nazivom Paleyevi diferencijski skupovi,

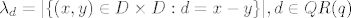
zasto iz 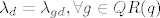slijedi da postoji lambda t.d. ?
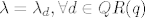to znaci da se svi elementi mogu dobiti kao gd, za d fiksan, ne?

_________________
Nov, još gluplji.

[Ignavia]

[Glupko_3.14]

zasto je d(Ham(r,q))=3?

zapravo ja nista ne razumijem u vezi tih Hammingovih kodova.
evo, npr u dokazu tm da vektori min tezine u Hammingovom kodu Ham(r,2) s parametrima (2^{r-1},2^r-1-r,3,1) tvore stupce incidencijske matrice 2-(2^r-1,3,1) dizajna:
trebamo provjeriti da kroz svake dvije tocke prolazi jedinstven blok
par tocaka shvatimo kao vektor y tezine 2 -> sad sam htjela pitat nesto zbog cega bi opet dobila , al ajde shvatila sam ovaj tren
postat cu jer sam dugo pisala post.
ne, zapravo slijedeci red mi nije jasan
w(y)=2 povlaci w(x)=3 gdje je x element Ham. koda t.d. y iz K(x,1)
ne, ipak mi je i to jasno.
ali kako znamo da je x jedinstven blok koji... i to mi je jasno
okej, ostaje pitanje s pocetka u vezi trojke

_________________
Nov, još gluplji.

[Gost]

Zašto je minimalna težina, a time i minimalna udaljenost jednaka 3?

Nema vektora težine 1 u kodu, jer postojanje takvog vektora značilo
bi da postoji nul-stupac u matrici ortogonalnog koda.
Nema ni vektora težine 2 u kodu, jer u protivnom linearna kombinacija neka dva stupca u ortogonalnom kodu bio bi nul-stupac, što bi značilo da su ta dva stupca linearno zavisna (a nema takvih).
Postoje vektori težine 3 jer u matrici ortogonalnog koda linearna kombinacija dva stupca opet je stupac te matrice (stupci te matrice su svi ne-nul stupci).

Postoji i općenita tvrdnja, za koju ne znam jeste li radili (vjerojatno jeste), da je minimalna težina koda jednaka d ako u matrici ortogonalnog koda postoji d linearno zavisnih stupaca, ali bilo kojih d-1 stupaca su linearno nezavisni.

[Glupko_3.14]

[Gost]

Ali, čuje se da je usmeni ipak dobro prošao .