| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 14:01 ned, 2. 9. 2007 Naslov: Postano: 14:01 ned, 2. 9. 2007 Naslov: |
    |
|
|
Pa ideja dokaza je da se prvo pronađe [latex]\Phi^{-1}[/latex] i na taj način se pokaže da je [latex]\Phi[/latex] bijekcija.
Znači, krenemo od neke funkcije [latex]\Psi\colon\{\overline{H} : \overline{H}\le \overline{G}\}\to\mathcal{P}(G)[/latex] definirane s [latex]\Psi(\overline{H}):=\pi^{-1}(\overline{H})=\{g\in G : gN\in\overline{H}\}[/latex]. A priori ne znamo da [latex]\Psi[/latex] preslikava podgrupe od [latex]\overline{G}[/latex] u podgrupe od [latex]G[/latex]. Znamo samo da ih preslikava u nekakve podskupove. Zato moramo pokazati da vrijedi (1):
Označimo [latex]H:=\Psi(\overline{H})[/latex]. Neka su [latex]x,y\in H[/latex]. To znači da su [latex]xN,yN\in\overline{H}[/latex]. No, kako je [latex]\overline{H}[/latex] grupa, slijedi da je [latex]xyN=(xN)(yN)\in\overline{H}[/latex]. To pak znači da je [latex]xy\in H[/latex]. Na isti način se dobije da je [latex]x^{-1}\in H[/latex] jer je [latex](xN)^{-1}=x^{-1}N[/latex]. Dakle, imamo [latex]H\le G[/latex].
Dalje se pokaže (2), tj. da je [latex]N\le H[/latex], no to je skroz očito jer je uvijek [latex]N\in\overline{H}[/latex] (to je neutralni element).
Još imaš (3), tj. da je [latex]\pi(H)=\overline{H}[/latex] jer je [latex]\pi[/latex] surjekcija.
Sad iz svega toga prvo zaključiš da kodomenu od [latex]\Psi[/latex] možeš smanjiti na [latex]\{H : H\le G\land N\le H\}[/latex] i konačno da je [latex]\Psi=\Phi^{-1}[/latex].
Nakon što dokažeš bijektivnost, ostaje ti dokazati da se normalne podgrupe preslikavaju u normalne. To ti je jasno?
Pa ideja dokaza je da se prvo pronađe 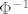 i na taj način se pokaže da je i na taj način se pokaže da je 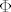 bijekcija. bijekcija.
Znači, krenemo od neke funkcije 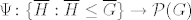 definirane s definirane s  . A priori ne znamo da . A priori ne znamo da  preslikava podgrupe od preslikava podgrupe od 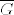 u podgrupe od u podgrupe od 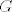 . Znamo samo da ih preslikava u nekakve podskupove. Zato moramo pokazati da vrijedi (1): . Znamo samo da ih preslikava u nekakve podskupove. Zato moramo pokazati da vrijedi (1):
Označimo 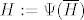 . Neka su . Neka su 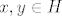 . To znači da su . To znači da su 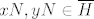 . No, kako je . No, kako je 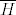 grupa, slijedi da je grupa, slijedi da je 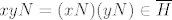 . To pak znači da je . To pak znači da je 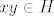 . Na isti način se dobije da je . Na isti način se dobije da je  jer je jer je 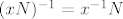 . Dakle, imamo . Dakle, imamo  . .
Dalje se pokaže (2), tj. da je  , no to je skroz očito jer je uvijek , no to je skroz očito jer je uvijek  (to je neutralni element). (to je neutralni element).
Još imaš (3), tj. da je 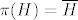 jer je jer je  surjekcija. surjekcija.
Sad iz svega toga prvo zaključiš da kodomenu od  možeš smanjiti na možeš smanjiti na 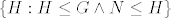 i konačno da je i konačno da je 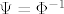 . .
Nakon što dokažeš bijektivnost, ostaje ti dokazati da se normalne podgrupe preslikavaju u normalne. To ti je jasno?
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
MystiC
Forumaš(ica)

Pridružen/a: 02. 10. 2005. (20:32:44)
Postovi: (CC)16
Spol: 
Lokacija: South of Heaven
|
|
| [Vrh] |
|
zzsan
Forumaš(ica)

Pridružen/a: 25. 11. 2005. (20:53:14)
Postovi: (89)16
|
 Postano: 15:24 ned, 2. 9. 2007 Naslov: Postano: 15:24 ned, 2. 9. 2007 Naslov: |
    |
|
|
[quote="MystiC"]evo imam i ja par pitanja
I) GRUPE
u dokazu 2.8 treceg teorema o izomorfizmu (strana 19) da li moram dokazivat da je jezgra M/N na ovaj nacin kao sto je u skripti ili mogu direktno iz definicije jezgre? Ker(pi-potez) = {gN | g € G, pi-potez(gN) = gM = e} = {gN | g € G, pi-potez(gN) = pi(g) = M}={gN | g € G, g € Ker(pi) = M} = M/N
II) PRSTENI
U dokazu propozicije 2.13 i) (strana 16) pise xRy podskup od P, onda je specijalno i x1y=xy podskup od P. ali sto ako R nema jedinicu? a nigdje ne pise u proizvoljnom prstenu s jedinicom[/quote]
Ovo prvo i mene zanima, a za ovo drugo ti na 7. stranici u poglavlju PRSTENI piše ovo:
[color=darkred]NAPOMENA. (1) Ako ne kažemo drukčije, od sada nadalje, u cijelom ovom poglavlju, smatramo
Prsten = Prsten s jedinicom 1.[/color]
:)
| MystiC (napisa): | evo imam i ja par pitanja
I) GRUPE
u dokazu 2.8 treceg teorema o izomorfizmu (strana 19) da li moram dokazivat da je jezgra M/N na ovaj nacin kao sto je u skripti ili mogu direktno iz definicije jezgre? Ker(pi-potez) = {gN | g € G, pi-potez(gN) = gM = e} = {gN | g € G, pi-potez(gN) = pi(g) = M}={gN | g € G, g € Ker(pi) = M} = M/N
II) PRSTENI
U dokazu propozicije 2.13 i) (strana 16) pise xRy podskup od P, onda je specijalno i x1y=xy podskup od P. ali sto ako R nema jedinicu? a nigdje ne pise u proizvoljnom prstenu s jedinicom |
Ovo prvo i mene zanima, a za ovo drugo ti na 7. stranici u poglavlju PRSTENI piše ovo:
NAPOMENA. (1) Ako ne kažemo drukčije, od sada nadalje, u cijelom ovom poglavlju, smatramo
Prsten = Prsten s jedinicom 1.

|
|
| [Vrh] |
|
Mad Wilson
Forumaš(ica)


Pridružen/a: 29. 05. 2006. (22:51:14)
Postovi: (121)16
|
 Postano: 22:00 ned, 2. 9. 2007 Naslov: Postano: 22:00 ned, 2. 9. 2007 Naslov: |
    |
|
|
Shvatio sam detalje...
Osim (3). Jesmo li tu dokazali da je Pi bijekcija za H?? (zbog surjektivnosti od Pi i definicije od H)?
Naime, ako se ne varam zgodno je razmisljati da preslikavanje Phi barata sa skupovima - ne elementima.
Ako se i dalje ne varam, ono sto smo mi uspijeli dokazati nakon (1), (2) i (3) je da je kanonski epimorfizam (dakle Pi) "skoro" pa bijekcija za skupove ?!?
Ako pak Pi restringiramo na {H | H<G & N<H} (element domene vise ne moze biti bas bilo koji skup, nego mora imati strukturu grupe i biti "nadgrupa" od N) i kodomenu suzimo na {H/N | H/N < G/N} (bas sliku od prethodno restringiranog Pi) injektivnost i surjektivnost slijede iz (3)??
I tako je modificirani Pi postao bijekcija i jednak upravo Phi. Ili mozda nije...??...
No, ocito se negdje varam, jer kaze Melkor "Nakon sto dokazes bijektivnost...".
Preslikavanje normalnih mi je jasno...
Sve u svemu Melkor karma++. Bas ti hvala.
Shvatio sam detalje...
Osim (3). Jesmo li tu dokazali da je Pi bijekcija za H?? (zbog surjektivnosti od Pi i definicije od H)?
Naime, ako se ne varam zgodno je razmisljati da preslikavanje Phi barata sa skupovima - ne elementima.
Ako se i dalje ne varam, ono sto smo mi uspijeli dokazati nakon (1), (2) i (3) je da je kanonski epimorfizam (dakle Pi) "skoro" pa bijekcija za skupove ?!?
Ako pak Pi restringiramo na {H | H<G & N<H} (element domene vise ne moze biti bas bilo koji skup, nego mora imati strukturu grupe i biti "nadgrupa" od N) i kodomenu suzimo na {H/N | H/N < G/N} (bas sliku od prethodno restringiranog Pi) injektivnost i surjektivnost slijede iz (3)??
I tako je modificirani Pi postao bijekcija i jednak upravo Phi. Ili mozda nije...??...
No, ocito se negdje varam, jer kaze Melkor "Nakon sto dokazes bijektivnost...".
Preslikavanje normalnih mi je jasno...
Sve u svemu Melkor karma++. Bas ti hvala.
|
|
| [Vrh] |
|
MystiC
Forumaš(ica)

Pridružen/a: 02. 10. 2005. (20:32:44)
Postovi: (CC)16
Spol: 
Lokacija: South of Heaven
|
|
| [Vrh] |
|
MystiC
Forumaš(ica)

Pridružen/a: 02. 10. 2005. (20:32:44)
Postovi: (CC)16
Spol: 
Lokacija: South of Heaven
|
|
| [Vrh] |
|
|








