| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Ally
Forumaš(ica)

Pridružen/a: 15. 04. 2008. (19:57:23)
Postovi: (7F)16
Spol: 
|
 Postano: 11:53 pet, 20. 6. 2008 Naslov: Postano: 11:53 pet, 20. 6. 2008 Naslov: |
    |
|
|
Otrogonalnu projekciju vektora x na potprostor M =[{m1, m2}] dobijes ovako: (korisitm primjer sa samo dva vektora u bazi da lakse objasnim, al isto je i za vise):
Napises da je x= a+b, pri cemu je a iz M, a b iz M(ortogonalno).
x=a+b skalarno pomnozis prvo sa m1, a onda sa m2. Svaki <b|mi>, gdje je i=1,2, ce ti biti 0, jer je b iz M(ortog.), a mi iz M.
A sad, buduci da je a iz M, moze se napisati kao linearna kombinacija vektora iz M, pa je a=ß1m1 + ß2m2.
Dobijes linearan sustav gdje su nepoznanice ß1,ß2, koji rjesavas tako da rijesis Gramovu matricu.
Sad izracunas a=ß1m1 + ß2m2 i onda mozes izracunati b=x-a. Ortogonalna projekcija vektora x na potprostor M jednaka je {a, b}.
Ima jos jedan nacin sa G-S postupkom, ali mislilm da je ovako jednostavnije.
Otrogonalnu projekciju vektora x na potprostor M =[{m1, m2}] dobijes ovako: (korisitm primjer sa samo dva vektora u bazi da lakse objasnim, al isto je i za vise):
Napises da je x= a+b, pri cemu je a iz M, a b iz M(ortogonalno).
x=a+b skalarno pomnozis prvo sa m1, a onda sa m2. Svaki <b|mi>, gdje je i=1,2, ce ti biti 0, jer je b iz M(ortog.), a mi iz M.
A sad, buduci da je a iz M, moze se napisati kao linearna kombinacija vektora iz M, pa je a=ß1m1 + ß2m2.
Dobijes linearan sustav gdje su nepoznanice ß1,ß2, koji rjesavas tako da rijesis Gramovu matricu.
Sad izracunas a=ß1m1 + ß2m2 i onda mozes izracunati b=x-a. Ortogonalna projekcija vektora x na potprostor M jednaka je {a, b}.
Ima jos jedan nacin sa G-S postupkom, ali mislilm da je ovako jednostavnije.
_________________
I just wanna dance..
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
ekatarina
Forumaš(ica)

Pridružen/a: 25. 11. 2007. (19:22:50)
Postovi: (161)16
Spol: 
|
|
| [Vrh] |
|
Ally
Forumaš(ica)

Pridružen/a: 15. 04. 2008. (19:57:23)
Postovi: (7F)16
Spol: 
|
|
| [Vrh] |
|
BitterSweet
Forumaš(ica)


Pridružen/a: 10. 10. 2007. (21:09:28)
Postovi: (174)16
Spol: 
Lokacija: sjeverno od raja
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
 Postano: 23:09 pon, 23. 6. 2008 Naslov: Postano: 23:09 pon, 23. 6. 2008 Naslov: |
    |
|
|
[quote="Spectre"]2. zadatak s prošlogodišnjeg kolokvija... Kako se rješava drugi dio zadatka, prikaz vektora [latex]x[/latex] u obliku [latex]x=a+b[/latex], pri čemu je [latex]a \epsilon M[/latex] i [latex]b \epsilon M^\perp[/latex][/quote]
Nađeš bazu za [latex]M^\perp[/latex] (pomoću [latex]x\in M^\perp \Leftrightarrow (x\perp m_1 \wedge x \perp m_2)[/latex] gdje su [latex]m_1[/latex] i [latex]m_2[/latex] vektori iz baze za [latex]M[/latex]), unija baza za [latex]M[/latex] i [latex]M^\perp[/latex] je baza za cijeli prostor (jer je [latex]M^\per[/latex] ortogonalni [b]komplement[/b]), prikažeš dani vektor u toj bazi, zbrojiš onaj dio koji pripada [latex]M[/latex] da dobiješ [latex]a[/latex]), zbrojiš ostalo da dobiješ [latex]b[/latex]). Uglavnom, ispadne [latex]a=(0, -\frac{7}{3}, \frac{7}{3}, \frac{14}{3} )[/latex]
| Spectre (napisa): | 2. zadatak s prošlogodišnjeg kolokvija... Kako se rješava drugi dio zadatka, prikaz vektora  u obliku u obliku 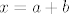 , pri čemu je , pri čemu je 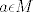 i i 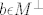 |
Nađeš bazu za 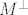 (pomoću (pomoću 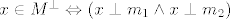 gdje su gdje su 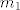 i i 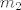 vektori iz baze za vektori iz baze za  ), unija baza za ), unija baza za  i i 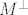 je baza za cijeli prostor (jer je je baza za cijeli prostor (jer je 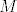 ortogonalni komplement), prikažeš dani vektor u toj bazi, zbrojiš onaj dio koji pripada ortogonalni komplement), prikažeš dani vektor u toj bazi, zbrojiš onaj dio koji pripada  da dobiješ da dobiješ  ), zbrojiš ostalo da dobiješ ), zbrojiš ostalo da dobiješ 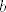 ). Uglavnom, ispadne ). Uglavnom, ispadne 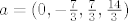
_________________
Nikola Adžaga
Građevinski fakultet, Sveučilište u Zagrebu
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
|












