| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 16:16 sri, 25. 6. 2008 Naslov: Postano: 16:16 sri, 25. 6. 2008 Naslov: |
    |
|
|
Pod 2) sam skužio, samo zamjena varijabli, (x,y)=F(u,v) i onda tm o zamjeni varijabli daje tvrdnju... ajde alene, sjeti se kak ostalo ide :beg:
:D
Pod 2) sam skužio, samo zamjena varijabli, (x,y)=F(u,v) i onda tm o zamjeni varijabli daje tvrdnju... ajde alene, sjeti se kak ostalo ide 

_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 10:24 čet, 26. 6. 2008 Naslov: Postano: 10:24 čet, 26. 6. 2008 Naslov: |
    |
|
|
Skužih i pod 1) uz pomoć kolegica j.b.i.n.s.h i queen:
Ide isto zamjena varijabli... krene se od desne strane, raspiše se F*(w) po definiciji, rastavi se rub od I^2 na one glatke puteve (njih je 4) i onda na svakom od tih integrala zamjenu varijabli F(u,v)=(x,y). Dobije se točno w u svakom od njih, pa se opet spoje svi integrali u integral po rubu od D.
8)
Skužih i pod 1) uz pomoć kolegica j.b.i.n.s.h i queen:
Ide isto zamjena varijabli... krene se od desne strane, raspiše se F*(w) po definiciji, rastavi se rub od I^2 na one glatke puteve (njih je 4) i onda na svakom od tih integrala zamjenu varijabli F(u,v)=(x,y). Dobije se točno w u svakom od njih, pa se opet spoje svi integrali u integral po rubu od D.

_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
dosed_girl
Forumaš(ica)

Pridružen/a: 04. 12. 2006. (21:01:46)
Postovi: (6F)16
Spol: 
Lokacija: -zG-
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
dosed_girl
Forumaš(ica)

Pridružen/a: 04. 12. 2006. (21:01:46)
Postovi: (6F)16
Spol: 
Lokacija: -zG-
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Fisher
Forumaš(ica)

Pridružen/a: 09. 02. 2007. (23:38:24)
Postovi: (41)16
Lokacija: split
|
 Postano: 23:37 sri, 9. 7. 2008 Naslov: Postano: 23:37 sri, 9. 7. 2008 Naslov: |
    |
|
|
@prvo pitanje: kao problem u dokazu je što se primjenjuje onaj korolar za neki "dobar" skup C, a naš C ne mora biti dobar -> dakle, nužno je provjerit integrabilnost funkcije f nad C, jer se u dokazu teorema samo pretpostavi da je f integrabilna nad C, a u iskazu se samo spominje neprekidnost od f.
I to nije u suprotnosti s Lebesgueovim teoremom jer tm govori o funkciji definiranoj na pravokutniku. I tu ti je uvik kontraprimjer za C := Qpresjek[0,1].. Znači, ono što treba napraviti je dokazati skup prekida od f sadržan u rubu od C (jer je rub od C mjere 0 pa je i svaki njegov podskup mjere 0).. I to sad dokazuješ preko karakteristične funkcije od C i treba dokazati da je skup prekida te karakt. fje baš jednak rubu od C..
I onda ide ono rastavljanje na dvije inkluzije, nadam se da to imaš u bilježnici, jer tako sve meni piše..
@drugo pitanje: prvo opaska, u skripti je krivo. Naime, nije rub od L(C) sadržan u L(V)/L(U) nego L(V)/L(Int U). To je prof posebno napomenula zato to zapamti. Da ne vrijedi ono tvoje, uzmi kao kontraprimjer da ti je C=A, L=id, U=A=V, rubC=rubA podskup V/U=prazanSkup što dovodi do kontradikcije.
A onda je ideja da L(V)/L(Int U) staviš u neki pravokutnik B, onda gledaš P' subdiviziju od B i za taj B nađeš pokrivač čija je suma manja od unaprijed zadanog epsilona i tad si dokazao da ti je skup L(V)/L(Int U) skup površine nula. Sad je rub od L(C) sadržan u tom skupu pa je nužno i on mjere 0, što je trebalo i dokazati..
Nadam se da je išta pomoglo..
@prvo pitanje: kao problem u dokazu je što se primjenjuje onaj korolar za neki "dobar" skup C, a naš C ne mora biti dobar → dakle, nužno je provjerit integrabilnost funkcije f nad C, jer se u dokazu teorema samo pretpostavi da je f integrabilna nad C, a u iskazu se samo spominje neprekidnost od f.
I to nije u suprotnosti s Lebesgueovim teoremom jer tm govori o funkciji definiranoj na pravokutniku. I tu ti je uvik kontraprimjer za C := Qpresjek[0,1].. Znači, ono što treba napraviti je dokazati skup prekida od f sadržan u rubu od C (jer je rub od C mjere 0 pa je i svaki njegov podskup mjere 0).. I to sad dokazuješ preko karakteristične funkcije od C i treba dokazati da je skup prekida te karakt. fje baš jednak rubu od C..
I onda ide ono rastavljanje na dvije inkluzije, nadam se da to imaš u bilježnici, jer tako sve meni piše..
@drugo pitanje: prvo opaska, u skripti je krivo. Naime, nije rub od L(C) sadržan u L(V)/L(U) nego L(V)/L(Int U). To je prof posebno napomenula zato to zapamti. Da ne vrijedi ono tvoje, uzmi kao kontraprimjer da ti je C=A, L=id, U=A=V, rubC=rubA podskup V/U=prazanSkup što dovodi do kontradikcije.
A onda je ideja da L(V)/L(Int U) staviš u neki pravokutnik B, onda gledaš P' subdiviziju od B i za taj B nađeš pokrivač čija je suma manja od unaprijed zadanog epsilona i tad si dokazao da ti je skup L(V)/L(Int U) skup površine nula. Sad je rub od L(C) sadržan u tom skupu pa je nužno i on mjere 0, što je trebalo i dokazati..
Nadam se da je išta pomoglo..
_________________
.. sve bi seke ljubile mornare, ali mame, mame brane to ..
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 8:08 čet, 10. 7. 2008 Naslov: Postano: 8:08 čet, 10. 7. 2008 Naslov: |
    |
|
|
Tnx Fisher :karma:
Al kad kažeš
[quote="Fisher"]@prvo pitanje: kao problem u dokazu je što se primjenjuje onaj korolar za neki "dobar" skup C, a naš C ne mora biti dobar [/quote]
mislim da mi ipak imamo dobar skup C u iskazu tm, tj skup koji je kompaktan, povezan i površine veće od 0. A to Qpresjek[0,1] nije. Tak da mislim da je tu komentar išo samo da se dokaže da nam je 'ljepota' od C nužna u ovom tm. :D
I imam još jedno pitanje... kod dokaza Darbouxovog tm, kod 1->2 smjera, u sripti kaže
analogno, intsuma>=s(P)-E/2
Ja sam probo to raspisat pošto je analogno al sam zapeo.
Naime, kad se int suma rastavi na one dvije sume (ko kod prvog dijela dokaza) imamo recimo
[latex]\sum_{I}{f(x_{ij}) \cotd \nu(A_{ij}')} \geq s(P) = \sum_{i,j}{m_{ij} \cotd \nu(A_{ij})}[/latex]
E sad, sigurno nam vrijedi da je f(xij)>=mij , ali kod ovih površina imamo suprotan znak, tj <=. (jer je suma površina svij Aij' manja od sume svih Aij)
Probo sam to i u par koraka al uvijek mi je problem ta površina...
I ona druga suma ne znam kak je dobiveno da je >=-E/2...
Jel bi mogo netko to raspisat? :pray:
Tnx Fisher 
Al kad kažeš
| Fisher (napisa): | | @prvo pitanje: kao problem u dokazu je što se primjenjuje onaj korolar za neki "dobar" skup C, a naš C ne mora biti dobar |
mislim da mi ipak imamo dobar skup C u iskazu tm, tj skup koji je kompaktan, povezan i površine veće od 0. A to Qpresjek[0,1] nije. Tak da mislim da je tu komentar išo samo da se dokaže da nam je 'ljepota' od C nužna u ovom tm. 
I imam još jedno pitanje... kod dokaza Darbouxovog tm, kod 1→2 smjera, u sripti kaže
analogno, intsuma>=s(P)-E/2
Ja sam probo to raspisat pošto je analogno al sam zapeo.
Naime, kad se int suma rastavi na one dvije sume (ko kod prvog dijela dokaza) imamo recimo
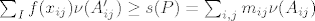
E sad, sigurno nam vrijedi da je f(xij)>=mij , ali kod ovih površina imamo suprotan znak, tj ⇐. (jer je suma površina svij Aij' manja od sume svih Aij)
Probo sam to i u par koraka al uvijek mi je problem ta površina...
I ona druga suma ne znam kak je dobiveno da je >=-E/2...
Jel bi mogo netko to raspisat? 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
5ra
Forumaš(ica)


Pridružen/a: 13. 08. 2006. (21:34:08)
Postovi: (D5)16
Spol: 
|
 Postano: 23:47 čet, 10. 7. 2008 Naslov: Postano: 23:47 čet, 10. 7. 2008 Naslov: |
    |
|
|
pa ak je površina skupa manja od epsilon, a površina skupa je integral funkcije lambda po tom skupu, onda je znači integral manji od epsilon. znači infimum svih gornjih Darbouxovim suma je manji od epsilon....
možda iz tog slijedi da možemo naći subdiviziju da je S(P) manje od epsilon, ali nisam baš sigurna... nekak mi to baš nije jasno.
[size=9][color=#999999]Added after 44 seconds:[/color][/size]
eh da, lema 17.17, zahvaljujući gornjim postovima uspjela sam dobiti 1) i 2) ali 3) nejde.... jel zna netko?
pa ak je površina skupa manja od epsilon, a površina skupa je integral funkcije lambda po tom skupu, onda je znači integral manji od epsilon. znači infimum svih gornjih Darbouxovim suma je manji od epsilon....
možda iz tog slijedi da možemo naći subdiviziju da je S(P) manje od epsilon, ali nisam baš sigurna... nekak mi to baš nije jasno.
Added after 44 seconds:
eh da, lema 17.17, zahvaljujući gornjim postovima uspjela sam dobiti 1) i 2) ali 3) nejde.... jel zna netko?
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
woodstock
Forumaš(ica)


Pridružen/a: 10. 11. 2006. (23:52:04)
Postovi: (99)16
Spol: 
|
 Postano: 18:36 sub, 12. 7. 2008 Naslov: Postano: 18:36 sub, 12. 7. 2008 Naslov: |
    |
|
|
[quote="Luuka"]I imam još jedno pitanje... kod dokaza Darbouxovog tm, kod 1->2 smjera, u sripti kaže
analogno, intsuma>=s(P)-E/2
Ja sam probo to raspisat pošto je analogno al sam zapeo.
Naime, kad se int suma rastavi na one dvije sume (ko kod prvog dijela dokaza) imamo recimo
[latex]\sum_{I}{f(x_{ij}) \cotd \nu(A_{ij}')} \geq s(P) = \sum_{i,j}{m_{ij} \cotd \nu(A_{ij})}[/latex]
E sad, sigurno nam vrijedi da je f(xij)>=mij , ali kod ovih površina imamo suprotan znak, tj <=. (jer je suma površina svih Aij' manja od sume svih Aij)
Probo sam to i u par koraka al uvijek mi je problem ta površina...
I ona druga suma ne znam kak je dobiveno da je >=-E/2...
[/quote]
Jesi saznao možda negdje odgovor na ovo? to i mene zanima već duže vrijeme...
| Luuka (napisa): | I imam još jedno pitanje... kod dokaza Darbouxovog tm, kod 1→2 smjera, u sripti kaže
analogno, intsuma>=s(P)-E/2
Ja sam probo to raspisat pošto je analogno al sam zapeo.
Naime, kad se int suma rastavi na one dvije sume (ko kod prvog dijela dokaza) imamo recimo
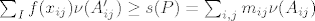
E sad, sigurno nam vrijedi da je f(xij)>=mij , ali kod ovih površina imamo suprotan znak, tj ⇐. (jer je suma površina svih Aij' manja od sume svih Aij)
Probo sam to i u par koraka al uvijek mi je problem ta površina...
I ona druga suma ne znam kak je dobiveno da je >=-E/2...
|
Jesi saznao možda negdje odgovor na ovo? to i mene zanima već duže vrijeme...
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 9:00 ned, 13. 7. 2008 Naslov: Postano: 9:00 ned, 13. 7. 2008 Naslov: |
    |
|
|
[quote="prof Hanzer u mailu"]Budući da tek sad odgovaram na vaš mail, bit ću vrlo kratka:
mislim da je najednostavnije da napravite analognu stvar, ali općenito
zamijenite ulogu particija P i P', onda ocijenjujete
s(P) s integralnom sumom po zajedničkim malim pravokutnicima za obje
particije, a onda po ostatku (skupina II) koje možete ocijeniti s
Mdelta O.
Pozdrav,
M. hanzer [/quote]
Al nije mi baš to pomoglo (a iskreno nisam ni bavio više time)...
| prof Hanzer u mailu (napisa): | Budući da tek sad odgovaram na vaš mail, bit ću vrlo kratka:
mislim da je najednostavnije da napravite analognu stvar, ali općenito
zamijenite ulogu particija P i P', onda ocijenjujete
s(P) s integralnom sumom po zajedničkim malim pravokutnicima za obje
particije, a onda po ostatku (skupina II) koje možete ocijeniti s
Mdelta O.
Pozdrav,
M. hanzer |
Al nije mi baš to pomoglo (a iskreno nisam ni bavio više time)...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
|





















