| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
DanijelM
Forumaš(ica)

Pridružen/a: 20. 02. 2008. (11:56:05)
Postovi: (29)16
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
Geliriell
Forumaš(ica)


Pridružen/a: 05. 10. 2005. (14:48:40)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
drcudo
Forumaš(ica)

Pridružen/a: 06. 03. 2008. (00:14:38)
Postovi: (17)16
Spol: 
|
 Postano: 21:09 sri, 25. 6. 2008 Naslov: Postano: 21:09 sri, 25. 6. 2008 Naslov: |
    |
|
|
Kada niko nece on ja!!
1.) u(x,y)= 2/3 *y -1/3 * x + (Exp[x/2 - y]*tg(4y - 2x) - 2/3 * y + 1/3 * x)Exp[y-2x]
2.) u(x,y)= sinx*cosy + xy - 1/2*y^2
3.) Vksi,eta + (2/eta - ksi)(Vksi -Veta)=0
4.) u(x,y)= 1/3 * y^2 +xy +1/4 * sin(x+y) - 3/4* sin(1/3 *y - x)
6.) u(t,x)= sinx * t * Exp[-t] + sinx * Exp[-t]
5.) u(,xt)= Suma_po_k_od_1_do_inf(Ck*Exp[-t*(3+4(k*pi/L)^2)]*sin(k*pi*x/L))
a gdje je Ck=Ak/Bk, gdje su
Ak= Integral_od_nule_do_L(sin(2*pi*x/L)*sin(k*pi*x/L)dx)
i
Bk=Integral_od_bule_do_L([sin(k*pi*x/L)]^2dx).
Bilo je jos pitanje sta sa onim 3u u 5.yadatku. nista.
Kuharica ti stima i za taj slucaj.kada stavis da ti je u(x,t)=X(x)T(t) i kada budes dijelio sa XT onda ces dobiti konstantu 3 koju uguras u jednadzbu yza T(jer je nizeg reda pa ti je lakse baratati tamo s njom nego u jednadzbama viseg reda kao sto bi to bilo da je pustis s X, no i tada se dobije isto rijesenje).
Malo je neuredsno ali kome treeba skuyit ce.
Sretno sutrra svima na kolokviju i puno srece.[latex][/latex][latex][/latex]
Kada niko nece on ja!!
1.) u(x,y)= 2/3 *y -1/3 * x + (Exp[x/2 - y]*tg(4y - 2x) - 2/3 * y + 1/3 * x)Exp[y-2x]
2.) u(x,y)= sinx*cosy + xy - 1/2*y^2
3.) Vksi,eta + (2/eta - ksi)(Vksi -Veta)=0
4.) u(x,y)= 1/3 * y^2 +xy +1/4 * sin(x+y) - 3/4* sin(1/3 *y - x)
6.) u(t,x)= sinx * t * Exp[-t] + sinx * Exp[-t]
5.) u(,xt)= Suma_po_k_od_1_do_inf(Ck*Exp[-t*(3+4(k*pi/L)^2)]*sin(k*pi*x/L))
a gdje je Ck=Ak/Bk, gdje su
Ak= Integral_od_nule_do_L(sin(2*pi*x/L)*sin(k*pi*x/L)dx)
i
Bk=Integral_od_bule_do_L([sin(k*pi*x/L)]^2dx).
Bilo je jos pitanje sta sa onim 3u u 5.yadatku. nista.
Kuharica ti stima i za taj slucaj.kada stavis da ti je u(x,t)=X(x)T(t) i kada budes dijelio sa XT onda ces dobiti konstantu 3 koju uguras u jednadzbu yza T(jer je nizeg reda pa ti je lakse baratati tamo s njom nego u jednadzbama viseg reda kao sto bi to bilo da je pustis s X, no i tada se dobije isto rijesenje).
Malo je neuredsno ali kome treeba skuyit ce.
Sretno sutrra svima na kolokviju i puno srece.[latex][/latex][latex][/latex]
|
|
| [Vrh] |
|
chiica
Forumaš(ica)

Pridružen/a: 03. 11. 2006. (20:13:17)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
vamotamo
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (18:49:29)
Postovi: (13)16
|
|
| [Vrh] |
|
L
Forumaš(ica)

Pridružen/a: 11. 02. 2007. (17:32:55)
Postovi: (17)16
|
 Postano: 23:59 sri, 25. 6. 2008 Naslov: Postano: 23:59 sri, 25. 6. 2008 Naslov: |
    |
|
|
Asistentica je rekla nešto u stilu da rješimo neke od onih zadataka koje je zadavala za domaću zadaću na vježbama, e al nisam skužila koliko ih treba rješit, nije baš bila precizna. Ja sam napisala dva, pa sad, valjda će bit ok .. Ako tko ima precizniji odgovor, i meni bi koristio ...
I predaju se na kolokviju..
Asistentica je rekla nešto u stilu da rješimo neke od onih zadataka koje je zadavala za domaću zadaću na vježbama, e al nisam skužila koliko ih treba rješit, nije baš bila precizna. Ja sam napisala dva, pa sad, valjda će bit ok .. Ako tko ima precizniji odgovor, i meni bi koristio ...
I predaju se na kolokviju..
|
|
| [Vrh] |
|
alen
Forumaš(ica)


Pridružen/a: 14. 10. 2005. (23:25:58)
Postovi: (221)16
|
|
| [Vrh] |
|
woodstock
Forumaš(ica)


Pridružen/a: 10. 11. 2006. (23:52:04)
Postovi: (99)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
woodstock
Forumaš(ica)


Pridružen/a: 10. 11. 2006. (23:52:04)
Postovi: (99)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 21:37 pet, 17. 4. 2009 Naslov: Postano: 21:37 pet, 17. 4. 2009 Naslov: |
    |
|
|
[quote="woodstock"]kak si ti to rješavao??meni nije nimalo slično. kaj se ne poništi sila reakcije sa Coriolisovom silom?[/quote]
Ja sam ovako:
Pošto tijelo rotira na konstantnoj visini, onda se sile ponište... imamo centripetalnu, silu reakcije i gravitacijsku... rotira po nekoj kružnici konstantnog radijusa, radijus se lako dobije ( R sqrt(3)/2, tj visina nekog tamo jednakostraničnog trokuta stranice R ). I onda silu reakcije rastavim na onu kolinearnu sa gravitacijom i onu kolinearnu sa centipetalnom... i dobim to kaj sam dobil...
Moguće da je krivo, a ako je, molim objašnjenje :D
| woodstock (napisa): | | kak si ti to rješavao??meni nije nimalo slično. kaj se ne poništi sila reakcije sa Coriolisovom silom? |
Ja sam ovako:
Pošto tijelo rotira na konstantnoj visini, onda se sile ponište... imamo centripetalnu, silu reakcije i gravitacijsku... rotira po nekoj kružnici konstantnog radijusa, radijus se lako dobije ( R sqrt(3)/2, tj visina nekog tamo jednakostraničnog trokuta stranice R ). I onda silu reakcije rastavim na onu kolinearnu sa gravitacijom i onu kolinearnu sa centipetalnom... i dobim to kaj sam dobil...
Moguće da je krivo, a ako je, molim objašnjenje 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
woodstock
Forumaš(ica)


Pridružen/a: 10. 11. 2006. (23:52:04)
Postovi: (99)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
greda5
Forumaš(ica)
Pridružen/a: 17. 04. 2009. (19:38:11)
Postovi: (26)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 21:32 sub, 18. 4. 2009 Naslov: Postano: 21:32 sub, 18. 4. 2009 Naslov: |
    |
|
|
[quote="greda5"]ej pozzz, može li mi netko reći kako je riješio 5. zadatak iz zadaće?
hvala[/quote]
Ja sam ovako (uz ispravak da je pravac po kojem se giba m1 ustvari y=-x+C za neki C):
[latex]x_1=x[/latex] , [latex]y_1=-x+C[/latex]
[latex]x_2=x + l \sin{\alpha}[/latex] , [latex]y_2=-x+C - l \cos{\alpha}[/latex] gdje je alfa kut između niti njihala i y-osi.
Nadalje, Fg=(0,-m1g,0,-m2g) pa je Ug=m1gy1+ m2gy2 pa se uvrste y1 i y2
[latex]U_{op}=\frac{1}{2}k (r-l)^2=\frac{1}{2}k (\sqrt{2 x^2-2Cx+C^2}-l)^2=\frac{1}{2}k ( 2 x^2-2Cx+C^2 + l^2 - 2l\sqrt{2 x^2-2Cx+C^2})[/latex]
I sad se nađe T, izračuna L i derivira i svašta i dobije se jako ružno.
Ako je krivo nek netko viče :D
| greda5 (napisa): | ej pozzz, može li mi netko reći kako je riješio 5. zadatak iz zadaće?
hvala |
Ja sam ovako (uz ispravak da je pravac po kojem se giba m1 ustvari y=-x+C za neki C):
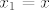 , , 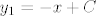
 , , 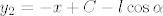 gdje je alfa kut između niti njihala i y-osi. gdje je alfa kut između niti njihala i y-osi.
Nadalje, Fg=(0,-m1g,0,-m2g) pa je Ug=m1gy1+ m2gy2 pa se uvrste y1 i y2
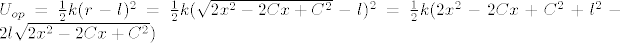
I sad se nađe T, izračuna L i derivira i svašta i dobije se jako ružno.
Ako je krivo nek netko viče 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
greda5
Forumaš(ica)
Pridružen/a: 17. 04. 2009. (19:38:11)
Postovi: (26)16
|
 Postano: 22:28 sub, 18. 4. 2009 Naslov: Postano: 22:28 sub, 18. 4. 2009 Naslov: |
    |
|
|
Ja sam ovako (uz ispravak da je pravac po kojem se giba m1 ustvari y=-x+C za neki C):
[latex]x_1=x[/latex] , [latex]y_1=-x+C[/latex]
[latex]x_2=x + l \sin{\alpha}[/latex] , [latex]y_2=-x+C - l \cos{\alpha}[/latex] gdje je alfa kut između niti njihala i y-osi.
Nadalje, Fg=(0,-m1g,0,-m2g) pa je Ug=m1gy1+ m2gy2 pa se uvrste y1 i y2
[latex]U_{op}=\frac{1}{2}k (r-l)^2=\frac{1}{2}k (\sqrt{2 x^2-2Cx+C^2}-l)^2=\frac{1}{2}k ( 2 x^2-2Cx+C^2 + l^2 - 2l\sqrt{2 x^2-2Cx+C^2})[/latex]
I sad se nađe T, izračuna L i derivira i svašta i dobije se jako ružno.
Ako je krivo nek netko viče :D[/quote]
hvala ti :)
Ja sam ovako (uz ispravak da je pravac po kojem se giba m1 ustvari y=-x+C za neki C):
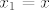 , , 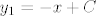
 , , 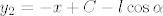 gdje je alfa kut između niti njihala i y-osi. gdje je alfa kut između niti njihala i y-osi.
Nadalje, Fg=(0,-m1g,0,-m2g) pa je Ug=m1gy1+ m2gy2 pa se uvrste y1 i y2
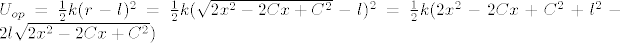
I sad se nađe T, izračuna L i derivira i svašta i dobije se jako ružno.
Ako je krivo nek netko viče  [/quote] [/quote]
hvala ti 
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:51 sub, 18. 4. 2009 Naslov: Postano: 22:51 sub, 18. 4. 2009 Naslov: |
    |
|
|
[quote="matmih"][quote="Luuka"][quote="woodstock"]a može se i izračunati kut, u tom istom trokutu iz kojeg dobiš radijus pa ti je onaj ctg=sqrt(3) :D[/quote]
E to mi je još falilo, i mislio sam da se može do tog doć, hvala! :D
[size=9][color=#999999]Added after 15 minutes:[/color][/size]
E da, kak doć do toga? :oops: Ne vidim...
Moja slika u attachmentu...[/quote]
Dobra ti je slikica. Možeš recimo: [latex]\displystyle sin \alpha =\frac{\frac{R}{2}}{R}[/latex] pa je [latex]\displaystyle sin \alpha= \frac{1}{2} \Rightarrow \alpha =\frac{\pi}{6} [/latex][/quote]
Hm, to bi bilo kada bi N išao skroz do središta sfere... a da li ide? :grebgreb:
| matmih (napisa): | | Luuka (napisa): | | woodstock (napisa): | a može se i izračunati kut, u tom istom trokutu iz kojeg dobiš radijus pa ti je onaj ctg=sqrt(3)  |
E to mi je još falilo, i mislio sam da se može do tog doć, hvala! 
Added after 15 minutes:
E da, kak doć do toga?  Ne vidim... Ne vidim...
Moja slika u attachmentu... |
Dobra ti je slikica. Možeš recimo: 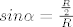 pa je pa je 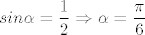 |
Hm, to bi bilo kada bi N išao skroz do središta sfere... a da li ide? 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|















